Conquista La Búsqueda De Cadenas Con El Algoritmo Aho-Corasick

La manipulación de cadenas y la búsqueda de patrones en ellas son tareas fundamentales en la ciencia de datos, y una tarea típica para cualquier programador.

Los algoritmos de cuerdas eficientes desempeñan un papel importante en muchos procesos de ciencia de datos. A menudo son lo que hacen que dichos procesos sean lo suficientemente factibles para su uso práctico.

En este artículo, aprenderás sobre uno de los algoritmos más potentes para buscar patrones en una gran cantidad de texto: el algoritmo Aho-Corasick. Este algoritmo utiliza una estructura de datos trie (pronunciado “try”) para realizar un seguimiento de los patrones de búsqueda y utiliza un simple método para encontrar eficientemente todas las ocurrencias de un conjunto dado de patrones en cualquier burbuja de texto.

Un artículo anterior sobre el Toptal Engineering Blog demostró un algoritmo de búsqueda de cadenas para el mismo problema. El enfoque adoptado en este artículo ofrece una mejor complejidad computacional.

El algoritmo Knuth-Morris-Pratt (KMP)

Para comprender cómo podemos buscar múltiples patrones en un texto de manera eficiente, primero tenemos que abordar un problema más fácil: buscar un patrón único en un texto dado.

Supongamos que tenemos una gran mancha de texto de longitud N y un patrón (que queremos buscar en el texto) de longitud M. Si queremos buscar una sola ocurrencia de este patrón, o todas las ocurrencias, podemos lograr una complejidad computacional de O(N + M) usando el algoritmo KMP.

Función de prefijo

El algoritmo KMP funciona calculando una función de prefijo del patrón que estamos buscando. La función de prefijo calcula previamente una posición alternativa para cada prefijo del patrón.

Definamos nuestro patrón de búsqueda como una cadena, etiquetada como S. Para cada subcadena S [0..i], donde i> = 1, encontraremos el prefijo máximo de esta cadena que también es el sufijo de esta cadena. Marcaremos la longitud de este prefijo P [i].

Para el patrón “abracadabra”, la función de prefijo produciría las siguientes posiciones de respaldo:

La función de prefijo identifica una característica interesante del patrón.

Tomemos un prefijo particular del patrón como ejemplo: “abracadab”. El valor de la función de prefijo para este prefijo es dos. Esto indica que para este prefijo “abracadab”, existe un sufijo de longitud dos que coincide exactamente con el prefijo de longitud dos (es decir, el patrón comienza con “ab” y el prefijo termina con “ab”). Además, esto es la coincidencia más larga para este prefijo.

Implementación

Aquí hay una función C # que se puede usar para calcular la función de prefijo para cualquier cadena:

public int[] CalcPrefixFunction(String s)
{
    int[] result = new int[s.Length]; // matriz con valores de función de prefijo

    result[0] = 0; // la función de prefijo siempre es cero para el primer símbolo (su caso degenerado)
    int k = 0; // valor actual de la función de prefijo
    para (int i = 1; i < s.Length; i++)
    {
      // Estamos saltando por valores de función de prefijo para probar prefijos más pequeños
      // El salto se detiene cuando encontramos una coincidencia, o llega a cero
      // Caso 2 si nos detenemos en un prefijo de longitud cero
      // Caso 3 si nos detenemos en un partido
        while (k > 0 && s[i] != s[k]) k = result[k - 1];
        if (s[k] == s[i]) k++; // hemos encontrado el prefijo más largo - caso 1
        result[i] = k; // almacenar este resultado en la matriz
    }

    resultado de devolución;
}

Al ejecutar esta función en un patrón un poco más largo, “abcdabcabcdabcdab” produce esto:

Complejidad computacional

A pesar de que hay dos bucles anidados, la complejidad de la función de prefijo es simplemente O (M), donde M es la longitud del patrón S.

Esto se puede explicar fácilmente al observar cómo funcionan los bucles.

Todas las iteraciones del bucle externo a través de i se pueden dividir en tres casos:

1. Aumenta k en uno. El ciclo completa una iteración.

2. No cambia el valor cero de k. El ciclo completa una iteración.

3. No cambia o disminuye un valor positivo de k.

Los primeros dos casos pueden ejecutarse como máximo M veces.

Para el tercer caso, definamos P (s, i) = k1 y P (s, i + 1) = k2, k2 <= k1. Cada uno de estos casos debe ir precedido de las ocurrencias k1 - k2 del primer caso. El conteo de disminuciones no excede k1 - k2 + 1. Y en total no tenemos más de 2 * M iteraciones.

Explicación del segundo ejemplo

Veamos el segundo patrón de ejemplo “abcdabcabcdabcdab”. Así es como la función de prefijo lo procesa, paso a paso:

1. Para una subcadena vacía y la subcadena “a” de longitud uno, el valor de la función de prefijo se establece en cero. (k = 0)

2. Mira la subcadena “ab”. El valor actual de k es cero y el carácter” b “no es igual al carácter” a “. Aquí, tenemos el segundo caso de la sección anterior. El valor de k se mantiene en cero y el valor de la función de prefijo para la subcadena” ab “también es cero.

3. Es el mismo caso para las subcadenas “abc” y “abcd”. No hay prefijos que también sean los sufijos de estas subcadenas. El valor para ellos permanece en cero.

4. Ahora veamos un caso interesante, la subcadena “abcda”. El valor actual de k sigue siendo cero, pero el último carácter de nuestra subcadena coincide con su primer carácter. Esto desencadena la condición de s [k] == s [i], donde k == 0 y i == 4. La matriz tiene índice cero y k es el índice del siguiente carácter para el prefijo de longitud máxima. Esto significa que hemos encontrado el prefijo de máxima longitud para nuestra subcadena que también es un sufijo. Tenemos el primer caso, donde el nuevo valor de k es uno, y por lo tanto, el valor de la función de prefijo P (“ abcda “) es uno.

5. El mismo caso también ocurre para las siguientes dos subcadenas, P (“abcdab”) = 2 y P (“abcdabc”) = 3. Aquí, estamos buscando nuestro patrón en el texto, comparando cadenas carácter por carácter. Digamos que los primeros siete caracteres del patrón coinciden con unos siete caracteres consecutivos de texto procesado, pero en el octavo carácter no coincide. ¿Qué debería pasar después? En el caso de una coincidencia de cadena ingenua, deberíamos devolver siete caracteres y comenzar nuevamente el proceso de comparación desde el primer carácter de nuestro patrón. Con el valor de la función de prefijo (aquí P (“abcdabc”) = 3) sabemos que nuestro sufijo de tres caracteres ya coincide con tres caracteres de texto. Y si el siguiente carácter en el texto es “d”, la longitud de la subcadena coincidente de nuestro patrón y subcadena en el texto se incrementa a cuatro (“abcd”). De lo contrario, P (“abc”) = 0 y comenzaremos el proceso de comparación desde el primer carácter del patrón. Pero lo importante es que no volvemos durante el procesamiento del texto.

6. La siguiente subcadena es “abcdabca”. En la subcadena anterior, la función de prefijo era igual a tres. Esto significa que k = 3 es mayor que cero, y al mismo tiempo tenemos una falta de coincidencia entre el siguiente carácter en el prefijo (s [k] = s [3] = "d") y el siguiente carácter en el sufijo (s [i] = s [7] ="a"). Esto significa que activamos la condición de s [k]! =S [i], y que el prefijo “abcd” no puede ser el sufijo de nuestra cadena. Deberíamos disminuir el valor de k y tomar el prefijo anterior para comparar, cuando sea posible. Como describimos anteriormente, la matriz tiene índice cero y k es el índice del siguiente carácter que verificamos desde el prefijo. El último índice del prefijo coincidente actualmente es k - 1. Tomamos el valor de la función de prefijo para el prefijo coincidente actualmente k = resultado [k - 1]. En nuestro caso (el tercer caso) la longitud del prefijo máximo se reducirá a cero y luego en la línea siguiente se aumentará hasta uno, porque “a” es el prefijo máximo que también es el sufijo de nuestra subcadena.

7. (Aquí continuamos nuestro proceso de cálculo hasta que lleguemos a un caso más interesante).

8. Comenzamos a procesar la siguiente subcadena: “abcdabcabcdabcd”. El valor actual de k es siete. Como con “abcdabca” arriba, hemos golpeado un no-partido: Debido a que el carácter “a” (el séptimo carácter) no es igual al carácter “d”, la subcadena “abcdabca” no puede ser el sufijo de nuestra cadena. Ahora obtenemos el valor ya calculado de la función de prefijo para “abcdabc” (tres) y ahora tenemos una coincidencia: el prefijo “abcd” también es el sufijo de nuestra cadena. Su prefijo máximo y el valor de la función de prefijo para nuestra subcadena son cuatro, porque ese es el valor actual de k.

9. Continuamos este proceso hasta el final del patrón.

En resumen: ambos ciclos no toman más de 3 M iteraciones, lo que demuestra que la complejidad es O (M). El uso de la memoria también es O (M).

Implementación de Algoritmo KMP

public int KMP(String text, String s)
{
	int[] p = CalcPrefixFunction(s); // Calcular la función de prefijo para una cadena de patrón

         // La idea es la misma que en la función de prefijo descrita anteriormente, pero ahora
        // estamos comparando prefijos de texto y patrón.


// El valor del prefijo de longitud máxima de la cadena del patrón que se encontró
// en el texto:

	int maxPrefixLength = 0;
	for (int i = 0; i < text.Length; i++)
	{
              // Como en la función de prefijo, estamos saltando por prefijos hasta que k sea
             // mayor que 0 o encontramos un prefijo que tiene coincidencias en el texto.

		while (maxPrefixLength > 0 && text[i] != s[maxPrefixLength])
            maxPrefixLength = p[maxPrefixLength - 1]; 

          // Si ocurrió una coincidencia, aumenta la longitud de la longitud máxima
         // prefijo.
		if (s[maxPrefixLength] == text[i]) maxPrefixLength++;

         // Si la longitud del prefijo tiene la misma longitud que la cadena del patrón,
         // significa que hemos encontrado una subcadena coincidente en el texto.

		if (maxPrefixLength == s.Length)
		{
			// Podemos devolver este valor o realizar esta operación.
			int idx = i - s.Length + 1;
            
            // Obtenga el prefijo de longitud máxima anterior y continúe la búsqueda.
			maxPrefixLength = p[maxPrefixLength - 1];
		}
	}

	return -1;
}

El algoritmo anterior itera a través del texto, carácter por carácter, e intenta aumentar el prefijo máximo tanto para nuestro patrón como para una secuencia de caracteres consecutivos en el texto. En caso de falla, no regresaremos a nuestra posición anterior en el texto. Conocemos el prefijo máximo de la subcadena encontrada del patrón; este prefijo es también el sufijo de esta subcadena encontrada y podemos simplemente continuar la búsqueda.

La complejidad de esta función es la misma que para la función de prefijo, lo que hace que la complejidad computacional general O (N + M) con O (M) memoria.

Trivia: los métodos String.IndexOf () y String.Contains () en el framework .NET tienen un algoritmo con la misma complejidad bajo el capó.

El algoritmo de Aho-Corasick

Ahora queremos hacer lo mismo para múltiples patrones.

Supongamos que hay patrones M de longitudes L1, L2, …, Lm. Necesitamos encontrar todas las coincidencias de patrones de un diccionario en un texto de longitud N.

Una solución trivial sería tomar cualquier algoritmo de la primera parte y ejecutarlo ** M ** veces. Tenemos complejidad de O (N + L1 + N + L2 + … + N + Lm), es decir (M * N + L).

Cualquier prueba suficientemente seria mata este algoritmo.

Tomar un diccionario con las 1,000 palabras más comunes en inglés como patrones y usarlo para buscar la versión en inglés de “War and Peace” de Tolstoy tomaría bastante tiempo. El libro tiene más de tres millones de caracteres.

Si tomamos las 10,000 palabras más comunes en inglés, el algoritmo funcionará alrededor de 10 veces más lento. Obviamente en entradas mayores a esta, el tiempo de ejecución también crecerá.

Aquí es donde el algoritmo Aho-Corasick hace su magia.

La complejidad del algoritmo Aho-Corasick es O (N + L + Z), donde Z es el recuento de coincidencias. Este algoritmo fue inventado por Alfred V. Aho y Margaret J. Corasick en 1975.

Implementación

Aquí necesitamos un trie, y agregamos a nuestro algoritmo una idea similar a las funciones de prefijo descritas anteriormente. Calcularemos valores de función de prefijo para todo el diccionario.

Cada vértice en el trie almacenará la siguiente información:

public class Vertex
{
	public Vertex()
	{
		Children = new Hashtable();            
		Leaf = false;
		Parent = -1;
		SuffixLink = -1;
		WordID = -1;
		EndWordLink= -1;
	}

    // Enlaces a los vértices secundarios en el trie:
    // Clave: Un solo caracter
    // Valor: El ID del vértice
	public Hashtable Children;

    // Indica que una palabra del diccionario termina en este vértice
	public bool Leaf;

    // Enlace al vértice padre
	public int Parent;

    // Char que nos mueve desde el vértice padre al vértice actual
	public char ParentChar;

    // Enlace de sufijo del vértice actual (el equivalente de P [i] del algoritmo KMP)
	public int SuffixLink;

    // Enlace al vértice de hoja de la palabra de longitud máxima que podemos hacer con el prefijo actual
	public int EndWordLink;

    // Si el vértice es la hoja, guardamos el ID de la palabra
	public int WordID;
}

Hay varias formas de implementar enlaces secundarios. El algoritmo tendrá una complejidad de O (N + L + Z) en el caso de una matriz, pero esto tendrá un requisito de memoria adicional de O (L * q), donde q es la longitud del alfabeto, ya que esa es la cantidad máxima de hijos que un nodo puede tener.

Si usamos alguna estructura con O (log (q)) acceso a sus elementos, tenemos un requisito de memoria adicional de O (L), pero la complejidad del algoritmo completo será O((N + L) * log (q) + Z).

En el caso de una tabla hash, tenemos O (L) memoria adicional, y la complejidad de todo el algoritmo será O (N + L + Z).

Este tutorial utiliza una tabla hash porque también funcionará con diferentes conjuntos de caracteres, por ejemplo, caracteres chinos.

Ya tenemos una estructura para un vértice. A continuación, definiremos una lista de vértices e iniciaremos el nodo raíz del trie.

public class Aho
{
	List<Vertex> Trie;
	List<int> WordsLength;
	int size = 0;
	int root = 0;

	public Aho()
	{
		Trie = new List<Vertex>();
		WordsLength = new List<int>();
		Init();
	}

	private void Init()
	{
		Trie.Add(new Vertex())            
		size++;
	}
}

Luego agregamos todos los patrones al trie. Para esto, necesitamos un método para agregar palabras al trie:

public void AddString(String s, int wordID)
{
	int curVertex = root;
	for (int i = 0; i < s.Length; ++i) // Iteración sobre los caracteres de la cadena
	{
		char c = s[i];

		// Comprobando si un vértice con este borde existe en el trie:
		if (!Trie[curVertex].Children.ContainsKey(c))
		{
			Trie.Add(new Vertex());
			
			Trie[size].SuffixLink = -1; // If not - add vertex
			Trie[size].Parent = curVertex;
			Trie[size].ParentChar = c;
			Trie[curVertex].Children[c] = size;
			size++;
		}
		curVertex = (int)Trie[curVertex].Children[c]; //Mover al nuevo vértice en el trie
	}
	// Marque el final de la palabra y almacene su ID
	Trie[curVertex].Leaf = true;
	Trie[curVertex].WordID = wordID;
	WordsLength.Add(s.Length);
}

En este punto, todas las palabras de patrón están en la estructura de datos. Esto requiere una memoria adicional de O (L).

A continuación, debemos calcular todos los enlaces de sufijos y enlaces de entrada del diccionario.

Para que sea claro y simple de entender, voy a recorrer nuestro trie desde la raíz hasta las hojas y hacer cálculos similares a los que hicimos para el algoritmo KMP, pero a diferencia del algoritmo KMP, donde encontramos la longitud máxima prefijo que también era el sufijo de la misma subcadena, ahora vamos a encontrar el sufijo de máxima longitud de la subcadena actual que también es el prefijo de algún patrón en el trie. El valor de esta función no será la longitud del sufijo encontrado; será el enlace al último carácter del sufijo máximo de la subcadena actual. Esto es lo que quiero decir con el sufijo link de un vértice.

Procesaré vértices por niveles. Para eso, usaré un algoritmo búsqueda por anchura (BFS):

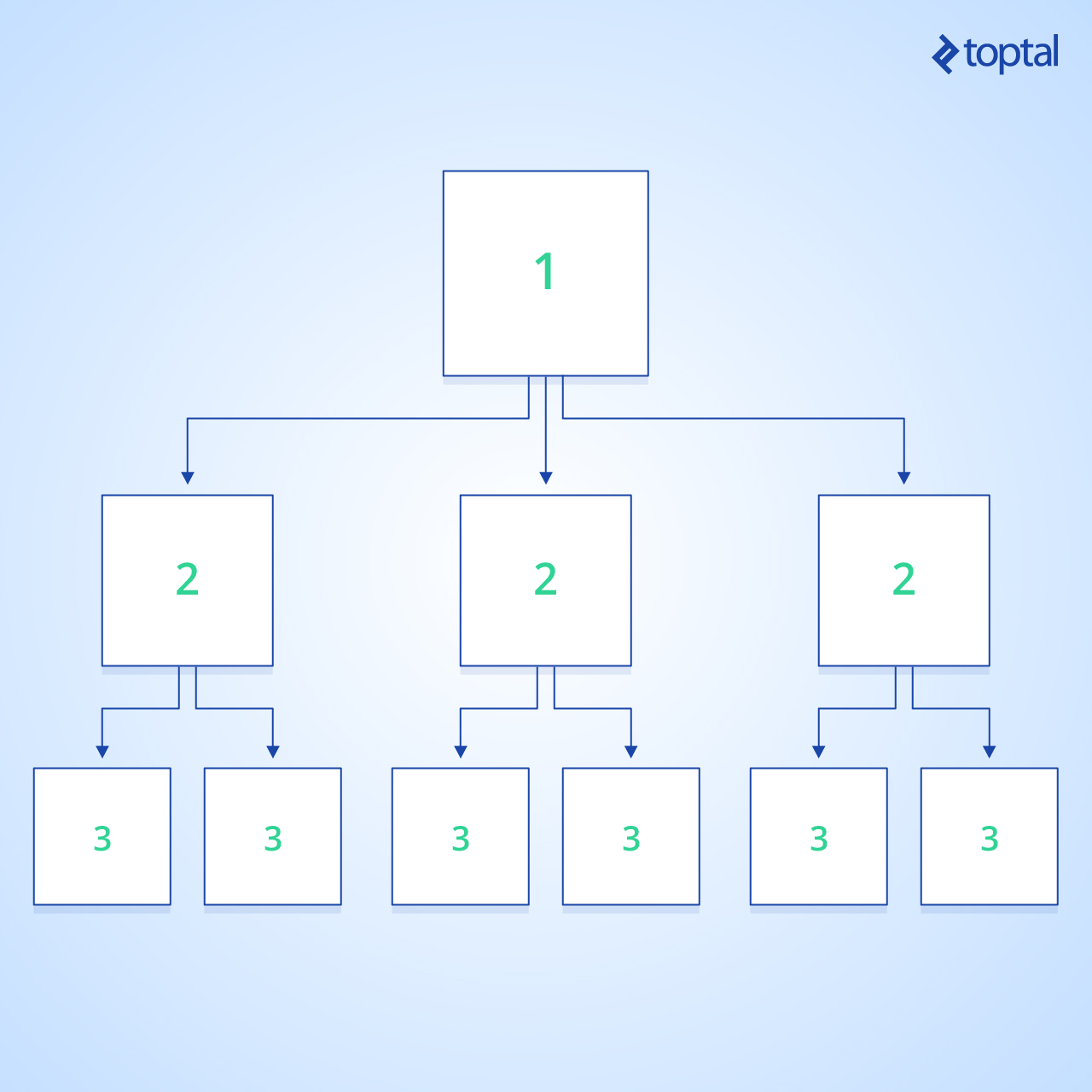
Y debajo está la implementación de este cruce:

public void PrepareAho()
{
	Queue<int> vertexQueue = new Queue<int>();
	vertexQueue.Enqueue(root);
	while (vertexQueue.Count > 0)
	{
		int curVertex = vertexQueue.Dequeue();
		CalcSuffLink(curVertex);

		foreach (char key in Trie[curVertex].Children.Keys)
		{
			vertexQueue.Enqueue((int)Trie[curVertex].Children[key]);
		}
	}
}

Y debajo está el método CalcSuffLink para calcular el enlace de sufijo para cada vértice (es decir, el valor de función de prefijo para cada subcadena en el trie):

public void CalcSuffLink(int vertex)
{
	// Processing root (empty string)
	if (vertex == root)
	{ 
		Trie[vertex].SuffixLink = root;
		Trie[vertex].EndWordLink = root;
		return;
	}
	// Procesamiento de hijos de la raíz (subcadenas de un caracter)
	if (Trie[vertex].Parent == root)
	{ 
		Trie[vertex].SuffixLink = root;
		if (Trie[vertex].Leaf) Trie[vertex].EndWordLink = vertex;
		else Trie[vertex].EndWordLink = Trie[Trie[vertex].SuffixLink].EndWordLink;
		return;
	}
// Los casos anteriores son casos degenerados en cuanto al cálculo de la función del prefijo; 
// el valor siempre es 0 y los enlaces al vértice raíz.

// Para calcular el sufijo link para el vértice actual, necesitamos el sufijo
// enlace para el padre del vértice y el personaje que nos movió a la
// vértice actual.
	int curBetterVertex = Trie[Trie[vertex].Parent].SuffixLink;
	char chVertex = Trie[vertex].ParentChar; 
// Desde este vértice y su subcadena comenzaremos a buscar el máximo
// prefijo para el vértice actual y su subcadena.

	
	while (true)
	{
// Si hay una ventaja con el carácter necesario, actualizamos nuestro enlace de sufijo
// y abandonar el ciclo
		if (Trie[curBetterVertex].Children.ContainsKey(chVertex))
		{
				Trie[vertex].SuffixLink = (int)Trie[curBetterVertex].Children[chVertex];
				break;
		}
// De lo contrario, estamos saltando por enlaces de sufijo hasta que lleguemos a la raíz
// (equivalente a k == 0 en el cálculo de la función de prefijo) o encontramos un
// mejor prefijo para la subserie actual.
		if (curBetterVertex == root)
		{ 
				Trie[vertex].SuffixLink = root;
				break;
		}
		curBetterVertex = Trie[curBetterVertex].SuffixLink; // Go back by sufflink
	}
	// Cuando completamos el cálculo del enlace de sufijo para el actual
// vertex, debemos actualizar el enlace al final de la palabra de longitud máxima
// que se puede producir a partir de la subcadena actual.
	if (Trie[vertex].Leaf) Trie[vertex].EndWordLink = vertex; 
	else Trie[vertex].EndWordLink = Trie[Trie[vertex].SuffixLink].EndWordLink;
}

La complejidad de este método es ** O (L) **; dependiendo de la implementación de la colección secundaria, la complejidad podría ser ** O (L * log (q)) **.

La prueba de complejidad es similar a la prueba de la función de prefijo de complejidad en el algoritmo KMP.

Veamos la siguiente imagen. Esta es una visualización del trie para el diccionario {abba, cab, baba, caab, ac, abac, bac} con toda su información calculada:

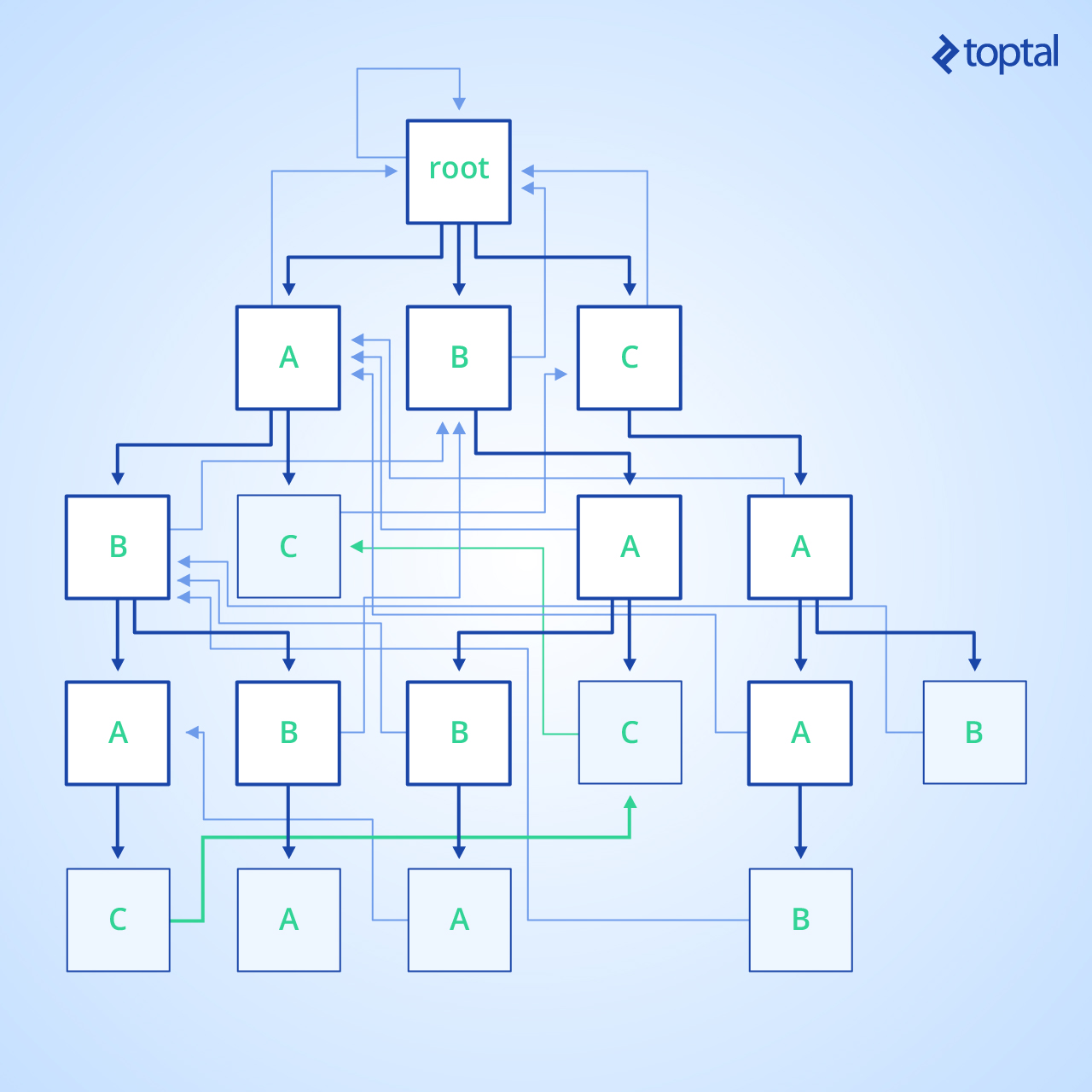
Los bordes de Trie son de color azul oscuro, los enlaces de sufijo son de color azul claro y los sufijos de diccionario están en verde. Los nodos correspondientes a las entradas del diccionario se resaltan en azul.

Y ahora solo necesitamos un método más: procesar un bloque de texto que pretendemos buscar:

public int ProcessString(String text)
{
	// Estado actual del valor
	int currentState = root;

	// Valor de resultado apuntado
	int result = 0;

	for (int j = 0; j < text.Length; j++)
	{
// Calculando nuevo estado en el trie
		while (true)
		{
			// Si tenemos la ventaja, entonces úsala
			if (Trie[currentState].Children.ContainsKey(text[j]))
			{
				currentState = (int)Trie[currentState].Children[text[j]];
				break;
			}
// De lo contrario, salta por los enlaces de sufijo e intenta encontrar el borde con
			// este caracter

// Si no hay posibles bordes eventualmente ascenderemos a
 // la raíz, y en este punto dejamos de verificar.
			if (currentState == root) break;
			currentState = Trie[currentState].SuffixLink;
		}
		int checkState = currentState;

		// Tratando de encontrar todas las palabras posibles de este prefijo
		while (true)
		{ 
			// Verificando todas las palabras que podemos obtener del prefijo actual
			checkState = Trie[checkState].EndWordLink;

			// Si estamos en el vértice raíz, no hay más coincidencias
			if (checkState == root) break;
			
// Si el algoritmo llegó a esta fila, significa que hemos encontrado un
// coincidencia de patrones. Y podemos hacer cálculos adicionales como encontrar
// el índice de la coincidencia encontrada en el texto. O comprueba que el encontrado
// patrón es una palabra separada y no solo, por ejemplo, una subcadena.

			result++;
			int indexOfMatch = j + 1 - WordsLength[Trie[checkState].WordID];
	
			// Tratando de encontrar todos los patrones combinados de menor longitud
			checkState = Trie[checkState].SuffixLink;
		}
	}

	return result;
}

Y, ahora esto está listo para usar:

En la entrada, tenemos una lista de patrones:

List<string> patterns;

Y buscar texto:

string text;

Y aquí como pegarlo todo junto:

// Inicia la estructura trie. Como parámetro opcional podemos poner el aproximado
// tamaño del trie para asignar memoria solo una vez para todos los nodos.
Aho ahoAlg = new Aho();

for (int i = 0; i < patterns.Count; i++)

{
    ahoAlg.AddString(patterns[i], i); // Add all patterns to the structure
}
// Preparar el algoritmo para el trabajo (calcula todos los enlaces en la estructura):
ahoAlg.PrepareAho();

// Procesar el texto. La salida puede ser diferente; en mi caso, es un recuento de
// partidos. En su lugar, podríamos devolver una estructura con información más detallada.
int countOfMatches = ahoAlg.ProcessString(text);

¡Y eso es! ¡Ahora sabes cómo funciona este algoritmo simple pero poderoso!

Aho-Corasick es realmente flexible. Los patrones de búsqueda no tienen que ser solo palabras, pero podemos usar oraciones enteras o cadenas de caracteres aleatorias.

Actuación

El algoritmo fue probado en un Intel Core i7-4702MQ.

Para las pruebas, tomé dos diccionarios: las 1,000 palabras más comunes en inglés y las 10,000 palabras más comunes en inglés.

Para agregar todas estas palabras al diccionario y preparar la estructura de datos para trabajar con cada uno de los diccionarios, el algoritmo requirió 55 ms y 135 ms, respectivamente.

El algoritmo procesó libros reales de 3-4 millones de caracteres de longitud dentro de 1.0-1.3 segundos, mientras que tomó 9.6 segundos para un libro con alrededor de 30 millones de caracteres.

Paralelizar el algoritmo Aho-Corasick

Ir en paralelo con el algoritmo Aho-Corasick no es un problema en absoluto:

Un texto grande se puede dividir en varios fragmentos y se pueden usar varios hilos para procesar cada fragmento. Cada hilo tiene acceso al trie generado basado en el diccionario.

¿Qué pasa con las palabras que se dividen en el límite entre los fragmentos? Este problema se puede resolver fácilmente.

Deja N ser la longitud de nuestro texto grande, S sea del tamaño de un fragmento, y L sea la longitud del patrón más grande en el diccionario.

Ahora podemos usar un truco simple. Dividimos los trozos con una superposición al final, por ejemplo tomando [S * (i - 1), S * i + L - 1], donde i es el índice del trozo. Cuando obtenemos una coincidencia de patrón, podemos obtener fácilmente el índice inicial de la coincidencia actual y simplemente verificar que este índice esté dentro del rango de fragmentos sin superposiciones, [S * (i - 1), S * i - 1].

Un algoritmo de búsqueda de cadenas versátil

El algoritmo Aho-Corasick es un potente algoritmo de combinación de cadenas que ofrece la mejor complejidad para cualquier entrada y no requiere mucha memoria adicional.

El algoritmo se utiliza a menudo en varios sistemas, como correctores ortográficos, filtros de correo no deseado, motores de búsqueda, búsqueda de bioinformática/secuencia de ADN, etc. De hecho, algunas herramientas populares que puede utilizar todos los días utilizan este algoritmo detrás de escena.

La función de prefijo del algoritmo KMP en sí misma es una herramienta interesante que reduce la complejidad de la coincidencia de patrón único al tiempo lineal. El algoritmo Aho-Corasick sigue un enfoque similar y utiliza una estructura de datos trie para hacer lo mismo para múltiples patrones.

Espero que hayas encontrado útil este tutorial sobre el algoritmo de Aho-Corasick.