Explorando Algoritmos de Aprendizaje Automático Supervisado
Si bien el aprendizaje automático suena muy técnico, una introducción a los métodos estadísticos involucrados te puede poner al día rápidamente. En este artículo, el ingeniero de software freelance de Toptal, Vladyslav Millier, explora algoritmos básicos de aprendizaje automático supervisado y scikit-learn, usándolos para predecir las tasas de supervivencia de los pasajeros del Titanic.
Si bien el aprendizaje automático suena muy técnico, una introducción a los métodos estadísticos involucrados te puede poner al día rápidamente. En este artículo, el ingeniero de software freelance de Toptal, Vladyslav Millier, explora algoritmos básicos de aprendizaje automático supervisado y scikit-learn, usándolos para predecir las tasas de supervivencia de los pasajeros del Titanic.
Vlad is a versatile software engineer with experience in many fields. He is currently perfecting his Scala and machine learning skills.
El objetivo principal de esta lectura es comprender suficiente metodología estadística para poder aprovechar los algoritmos de aprendizaje automático, lo cuales se encuentran en la biblioteca scikit-learn de Python y luego aplicar este conocimiento para resolver un problema clásico de aprendizaje automático.
La primera parada de nuestro viaje nos llevará a través de una breve historia del aprendizaje automático. Luego nos sumergiremos en diferentes algoritmos. En nuestra parada final, usaremos lo que aprendimos para resolver el Problema de predicción de la tasa de supervivencia del Titanic.
Algunos descargos de responsabilidad:
- Soy un ingeniero de software full-stack, no un experto en algoritmos de aprendizaje automático.
- Supongo que sabes algo básico Python.
- Esto es exploratorio, por lo que no todos los detalles se explican cómo sería en un tutorial.
Dicho esto, ¡comencemos!
Una Introducción Rápida a los Algoritmos de Aprendizaje Automático
Tan pronto como te aventuras en este campo, te das cuenta de que el aprendizaje automático es menos romántico de lo que piensas. Inicialmente, estaba lleno de esperanzas de que, después de aprender más, sería capaz de construir mi propia Jarvis de IA, que pasaría todo el día en software de codificación y haciendo dinero para mí, así podría pasar días enteros al aire libre leyendo libros, conduciendo una motocicleta, y disfrutando de un estilo de vida imprudente mientras mi Jarvis personal hace que mis bolsillos sean más profundos. Sin embargo, pronto me di cuenta de que la base de los algoritmos de aprendizaje automático son las estadísticas, que personalmente considero aburridas y poco interesantes. Afortunadamente, resultó que las estadísticas “aburridas” tienen algunas aplicaciones muy fascinantes.
Pronto descubrirás qué para llegar a esas fascinantes aplicaciones, necesitas comprender muy bien las estadísticas. Uno de los objetivos de los algoritmos de aprendizaje automático es encontrar dependencias estadísticas en los datos suministrados.
Los datos suministrados pueden ser desde controlar la presión arterial en comparación con la edad, hasta encontrar texto manuscrito basado en el color de varios píxeles.
Dicho esto, tenía curiosidad por ver si podía usar algoritmos de aprendizaje automático para encontrar dependencias en las funciones hash criptográficas (SHA, MD5, etc.)—sin embargo, no se puede hacer eso porque las primitivas criptográficas apropiadas se construyen en tal forma que eliminan dependencias y producen resultados significativamente difíciles de predecir. Creo que, dado un tiempo infinito, los algoritmos de aprendizaje automático podrían descifrar cualquier modelo criptográfico.
Desafortunadamente, no tenemos tanto tiempo, así que tenemos que encontrar otra manera de minar, de manera eficiente, la criptomoneda. ¿Qué tan lejos hemos llegado hasta ahora?
Una Breve Historia de los Algoritmos de Aprendizaje Automático
Las raíces de los algoritmos de aprendizaje automático provienen de Thomas Bayes, quien fue estadístico inglés y vivió en el siglo XVIII. Su artículo Un ensayo para resolver un problema en la doctrina de las oportunidades subyace el teorema de Bayes, que se aplica ampliamente en el campo de las estadísticas.
En el siglo XIX, Pierre-Simon Laplace publicó Théorie analytique des probabilités, ampliando el trabajo de Bayes y definiendo lo que conocemos hoy como el Teorema de Bayes. Poco antes, Adrien-Marie Legendre describió el método de “mínimos cuadrados”, que también se usa mucho hoy en día en el aprendizaje supervisado.
El siglo 20 es el período en que la mayoría de los descubrimientos conocidos públicamente se han realizado en este campo. Andrey Markov inventó las cadenas de Markov, que utilizó para analizar poemas. Alan Turing propuso una máquina de aprendizaje que podría volverse artificialmente inteligente, básicamente presagiando algoritmos genéticos. Frank Rosenblatt inventó el Perceptron, lo que desató una gran emoción y una gran cobertura en los medios.
Pero luego, en la década de 1970, se percibió un gran pesimismo en torno a la idea de la IA, y por lo tanto, la reducción de la financiación, por lo que este período se denomina “invierno”. El redescubrimiento de la retropropagación en los años ochenta provocó un resurgimiento en la investigación del aprendizaje automático. Y hoy, es un tema candente una vez más.
El fallecido Leo Breiman distinguía entre dos modelos de paradigma estadísticos. El “Modelado algorítmico” que significa más o menos, algoritmos de aprendizaje de máquina, parecido a bosque al azar.
Aprendizaje de máquina y estadísticas son campos relacionados. Según Michael I. Jordan, las ideas de aprendizaje de máquina, desde principios metodológicos a herramientas teóricas, han tenido una larga prehistoria en estadísticas. También sugería la data de ciencia como término estable para el problema general en el cual han estado trabajando los especialistas de aprendizaje de máquinas y estadistas.
Categorías de Algoritmos de Aprendizaje de Máquina
El campo de aprendizaje de máquina se establece en dos pilares principales llamados aprendizaje supervisado y aprendizaje no supervisado. Algunas personas también consideran un nuevo campo de estudio como el—aprendizaje profundo—que sea separado de la pregunta común de aprendizaje supervisado o no supervisado.
El aprendizaje supervisado se da cuando una computadora es presentada con ejemplos de entradas y sus salidas deseadas. La meta es aprender sobre fórmulas generales que mapea entradas a salidas. Esto se puede dividir de la siguiente manera:
- Aprendizaje semi-supervisado, se da cuando a la computadora se le da un entrenamiento incompleto acompañado de salidas faltantes
- Aprendizaje activo, se da cuando la computadora sólo puede obtener etiquetas de aprendizaje por un conjunto limitado de instancias. Cuando se usa de manera interactiva, sus conjuntos de entrenamiento se pueden presentar al usuario como etiquetado
- Aprendizaje de refuerzo, se da cuando la data de entrenamiento solo se otorga como retroalimentación a las acciones del programa en el ambiente dinámico, como manejar un vehículo o jugar un juego contra un oponente
En contraste, el aprendizaje no supervisado se da cuando no se otorgan etiquetas y queda de parte del algoritmo encontrar la estructura en su entrada. El aprendizaje no supervisado puede ser una meta en sí misma cuando sólo necesitamos descubrir patrones escondidos.
Aprendizaje profundo es un nuevo campo de estudio el cual está inspirado por la estructura y función del cerebro humano, de igual manera está basado en redes neurales artificiales en vez de sólo conceptos estadísticos. El aprendizaje profundo se puede usar en ambos acercamientos, supervisado y no supervisado.
En este artículo, veremos algunos de los algoritmos de aprendizaje de máquina supervisados más simples, y los usaremos para calcular las probabilidades de sobrevivencia de un individuo en el trágico hundimiento del titanic. Pero en general, si no estás seguro de que algoritmo usar, un buen lugar para comenzar es la hoja de repaso del algoritmo de aprendizaje de máquina de scikit-learn.
Modelos Básicos de Aprendizaje de Máquina Supervisado
Tal vez el algoritmo más sencillo es de regresión lineal. En ocasiones, éste puede ser representado gráficamente como una línea recta, pero a pesar de su nombre, si hay una hipótesis polinomial, esta línea podría ser una curva. En cualquier caso, modela las relaciones entre una variable dependiente escalar $y$ y uno o más valores explicativos denotados por $x$.
En términos de un laico, esto significa que la regresión lineal es el algoritmo que aprende la dependencia entre cada uno de los ya conocidos $x$ y $y$, tanto así que podemos usarlo para predecir $y$ para una muestra no conocida de $x$.
En nuestro primer ejemplo de aprendizaje supervisado, utilizaremos un modelo de regresión lineal básico para predecir la presión arterial de una persona, según su edad. Este es un set de data muy sencillo con dos características importantes: Edad y presión arterial.
Como ya lo mencionamos arriba, la mayoría de los algoritmos de aprendizaje de máquina funcionan al encontrar una dependencia estadística en la data que se les proporciona. Esta dependencia se llama una hipótesis y usualmente se denota por $h(\theta)$.
Para descifrar esta hipótesis, comencemos por descargar y explorar la data.
import matplotlib.pyplot as plt
from pandas import read_csv
import os
# Cargar datos
data_path = os.path.join(os.getcwd(), "data/blood-pressure.txt")
dataset = read_csv(data_path, delim_whitespace=True)
# Tenemos 30 entradas en nuestro set de data y cuatro características. La primera característica es la identificación de la entrada.
# La segunda característica siempre es la nro. 1. La tercera es la edad y la última es la presión arterial.
# Ahora dejaremos de lado la Identificación y la característica Uno por ahora, ya que no es importante.
dataset = dataset.drop(['ID', 'One'], axis=1)
# Y mostraremos esta gráfica
%matplotlib inline
dataset.plot.scatter(x='Age', y='Pressure')
# Ahora, asumiremos que ya sabemos la hipótesis y parece una línea recta
h = lambda x: 84 + 1.24 * x
# ahora agreguemos esta línea a la gráfica
ages = range(18, 85)
estimated = []
for i in ages:
estimated.append(h(i))
plt.plot(ages, estimated, 'b')
[<matplotlib.lines.Line2D at 0x11424b828>]
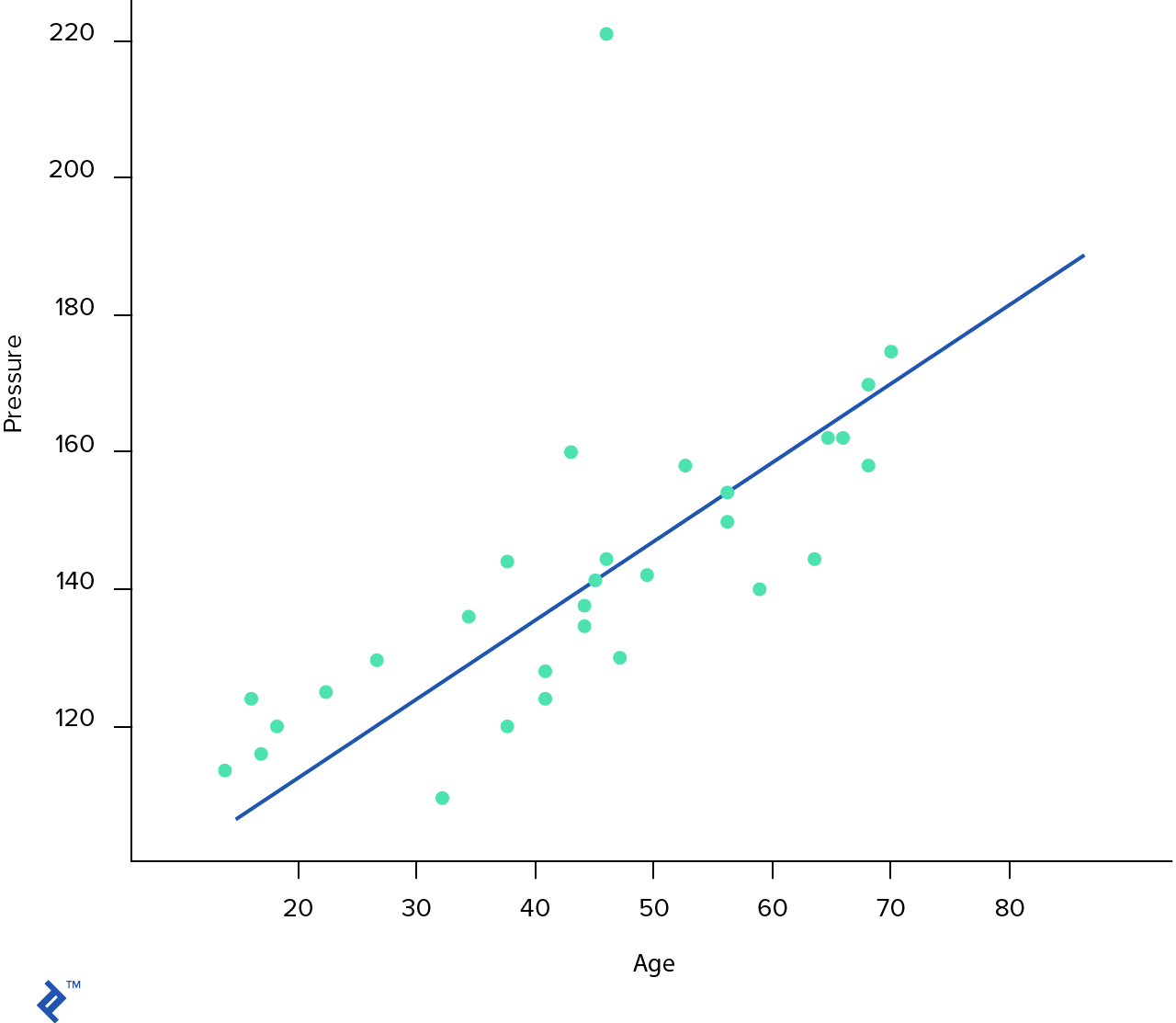
En la gráfica de arriba, cada punto azul representa nuestra data de muestra y la línea azul es la hipótesis que se debe aprender nuestro algoritmo. Entonces, ¿Cual es esta hipótesis?
Para resolver este problema, necesitamos aprender la dependencia entre $x$ y $y$, que se denota por $y = f(x)$. Por ende, $f(x)$ es la función objetivo ideal. El algoritmo de aprendizaje de máquina tratará de adivinar la función de la hipótesis $h(x)$, la cual es la aproximación más cercana del desconocido $f(x)$.
La forma más simple de hipótesis para el problema de regresión lineal se ve así: $h_\theta(x) = \theta_0 + \theta_1 * x$. Tenemos una variable escalar de entrada sencilla $x$, que da como salida una variable escalar sencilla $y$, donde $\theta_0$ y $\theta_1$ son parámetros que debemos aprender. El proceso de ajustar esta línea azul en la data se llama regresión lineal. Es importante entender que tenemos sólo un parámetro de entrada $x_1$; sin embargo, muchas de las funciones de hipótesis también incluirán una unidad con inclinación ($x_0$). Así que nuestra hipótesis resultante tiene una forma de $h_\theta(x) = \theta_0 * x_0 + \theta_1 * x_1$. Pero podemos evitar escribir $x_0$ porque casi siempre es igual a 1.
Volviendo a la línea azul. Nuestra hipótesis se ve así $h(x) = 84 + 1.24x$, lo cual significa que $\theta_0 = 84$ y $\theta_1 = 1.24$. ¿Cómo podemos derivar automáticamente esos valores $\theta$?
Necesitamos definir una función de costo. Esencialmente, lo que hace una función de costo es calcular el error de raíz al cuadrado entre el modelo de predicción y la salida como tal.
\[J(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2\]Por ejemplo, nuestra hipótesis predice que para alguien que tiene 48 años, su presión arterial debería ser de $h(48) = 84 + 1.24 * 48 = 143mmHg$; sin embargo, en nuestra muestra de entrenamiento, tenemos el valor de $130 mmHg$. Por lo tanto, el error es $(143 - 130)^2 = 169$. Ahora necesitamos calcular este error en cada entrada en nuestro set de data de entrenamiento, luego sumarlo todo ($\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2$) y tomar el valor significativo de ahí. Esto nos da un único número escalar, el cual representa el costo de la función. Nuestra meta es encontrar los valores $\theta$, para que la función de costo sea más baja; en otras palabras, queremos minimizar la función de costo. Esperemos que esto sea de manera intuitiva: si tenemos un valor de función de costo pequeña, esto significa que el error de predicción también sería bajo.
import numpy as np
# Calculemos el costo para la hipótesis de arriba
h = lambda x, theta_0, theta_1: theta_0 + theta_1 * x
def cost(X, y, t0, t1):
m = len(X) # the number of the training samples
c = np.power(np.subtract(h(X, t0, t1), y), 2)
return (1 / (2 * m)) * sum(c)
X = dataset.values[:, 0]
y = dataset.values[:, 1]
print('J(Theta) = %2.2f' % cost(X, y, 84, 1.24))
J(Theta) = 1901.95
Ahora, necesitamos encontrar los valores de $\theta$ tanto que el valor de nuestra función de costo es mínimo. ¿Pero cómo podemos hacer eso?
\[minJ(\theta) = \frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)}) - y^{(i)})^2\]Hay muchos algoritmos posibles, pero el más popular es gradiente por descenso. Para poder entender la intuición detrás del método descenso gradiente, pongámoslo primero en la gráfica. Por simplicidad, asumiremos una hipótesis más sencilla $h(\theta) = \theta_1 * x$. Luego, tendremos una gráfica 2D sencilla en la que $x$ es el valor de $\theta$ y $y$ es la función de costo en este punto.
import matplotlib.pyplot as plt
fig = plt.figure()
# Genera los datos
theta_1 = np.arange(-10, 14, 0.1)
J_cost = []
for t1 in theta_1:
J_cost += [ cost(X, y, 0, t1) ]
plt.plot(theta_1, J_cost)
plt.xlabel(r'$\theta_1$')
plt.ylabel(r'$J(\theta)$')
plt.show()
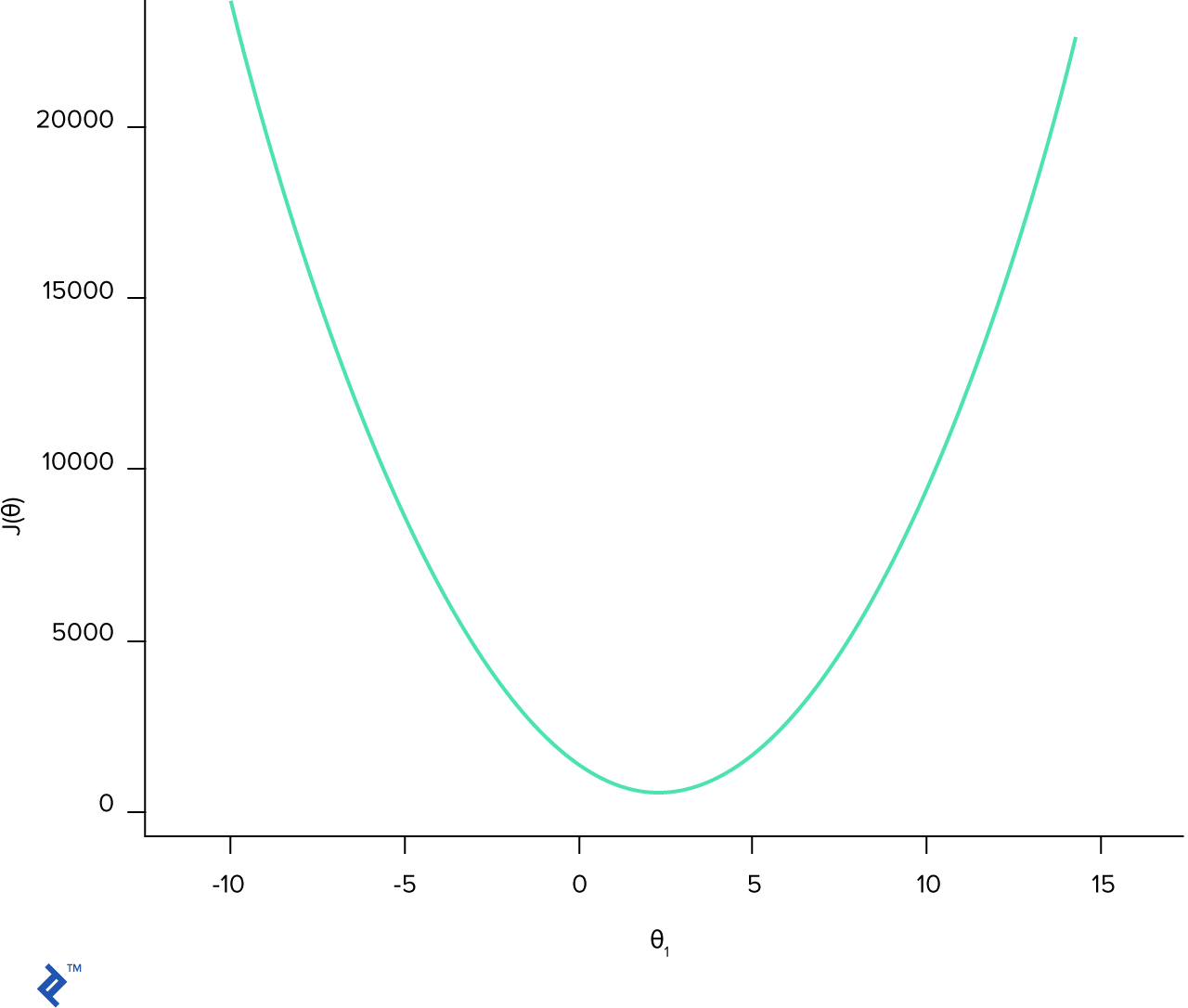
La función de costo es convexa, lo cual significa que en el intervalo $[a, b]$ hay sólo un mínimo. Lo cual significa que los mejores parámetros $\theta$ están en el punto donde la función de costo es mínima.
Básicamente, el descenso gradiente es un algoritmo que intenta encontrar un set de parámetros que minimiza la función. Comienza con un set inicial de parámetros y toma interactivamente da pasos hacia la dirección negativa de la función gradiente.
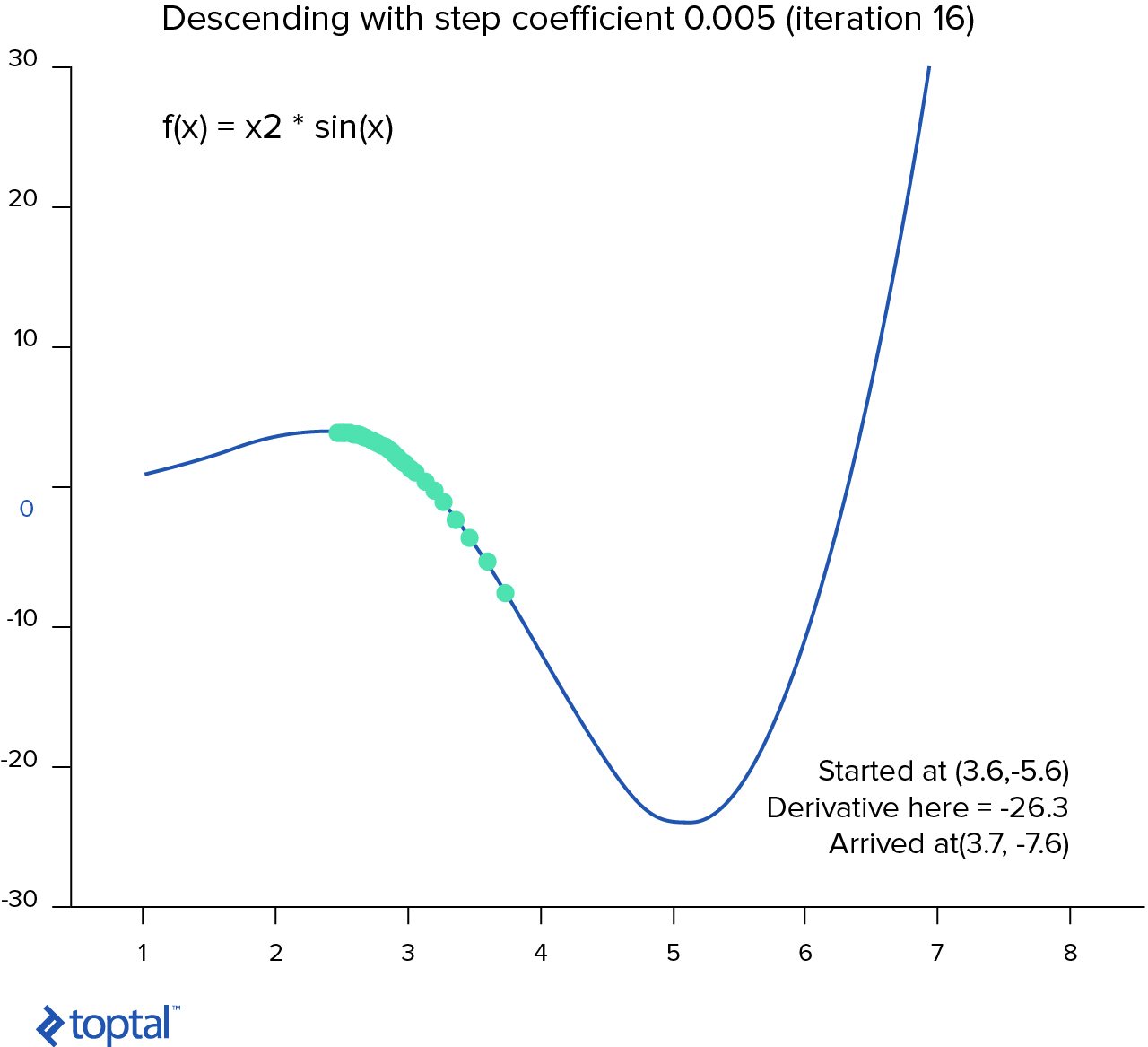
Si calculamos el derivado de una función de hipótesis en un punto específico, esto nos dará acceso directo a la línea tangente hacia la curva en ese punto. Esto significa que podemos calcular el acceso directo en cada punto de la gráfica.
La forma en la que trabaja el algoritmo es ésta:
- Escogemos un punto de comienzo al azar ($\theta$ al azar).
- Calcula la derivativa de la función de costo en este punto.
- Toma el paso pequeño hacia el acceso directo $\theta_j := \theta_j - \lambda * \frac{\partial}{\partial \theta_j} * J(\theta)$.
- Repite pasos 2-3 hasta la convergencia.
Ahora, la condición de convergencia depende en la implementación del algoritmo. Tal vez nos detengamos después de 50 pasos, después de algún lumbral o cualquier otra cosa.
import math
# Ejemplo del algoritmo simple de descenso gradiente tomado de Wikipedia
cur_x = 2.5 # The algorithm starts at point x
gamma = 0.005 # Step size multiplier
precision = 0.00001
previous_step_size = cur_x
df = lambda x: 2 * x * math.cos(x)
# Recuerda la curva de aprendizaje y establécela
while previous_step_size > precision:
prev_x = cur_x
cur_x += -gamma * df(prev_x)
previous_step_size = abs(cur_x - prev_x)
print("The local minimum occurs at %f" % cur_x)
El mínimo local pasa en 4.712194
No implementaremos esos algoritmos en este artículo. En vez de eso, utilizaremos el ya adoptado scikit-learn, una biblioteca de aprendizaje de máquina de fuente abierta Python. Proporciona muchas API útiles para diferentes problemas de minería de data y aprendizaje de máquina.
De sklearn.linear_model importar LinearRegression
# La Regresión Lineal usa el método de descenso gradiente
# Nuestra data
X = dataset[['Age']]
y = dataset[['Pressure']]
regr = LinearRegression()
regr.fit(X, y)
# Salidas Argumentadas
plt.xlabel('Age')
plt.ylabel('Blood pressure')
plt.scatter(X, y, color='black')
plt.plot(X, regr.predict(X), color='blue')
plt.show()
plt.gcf().clear()
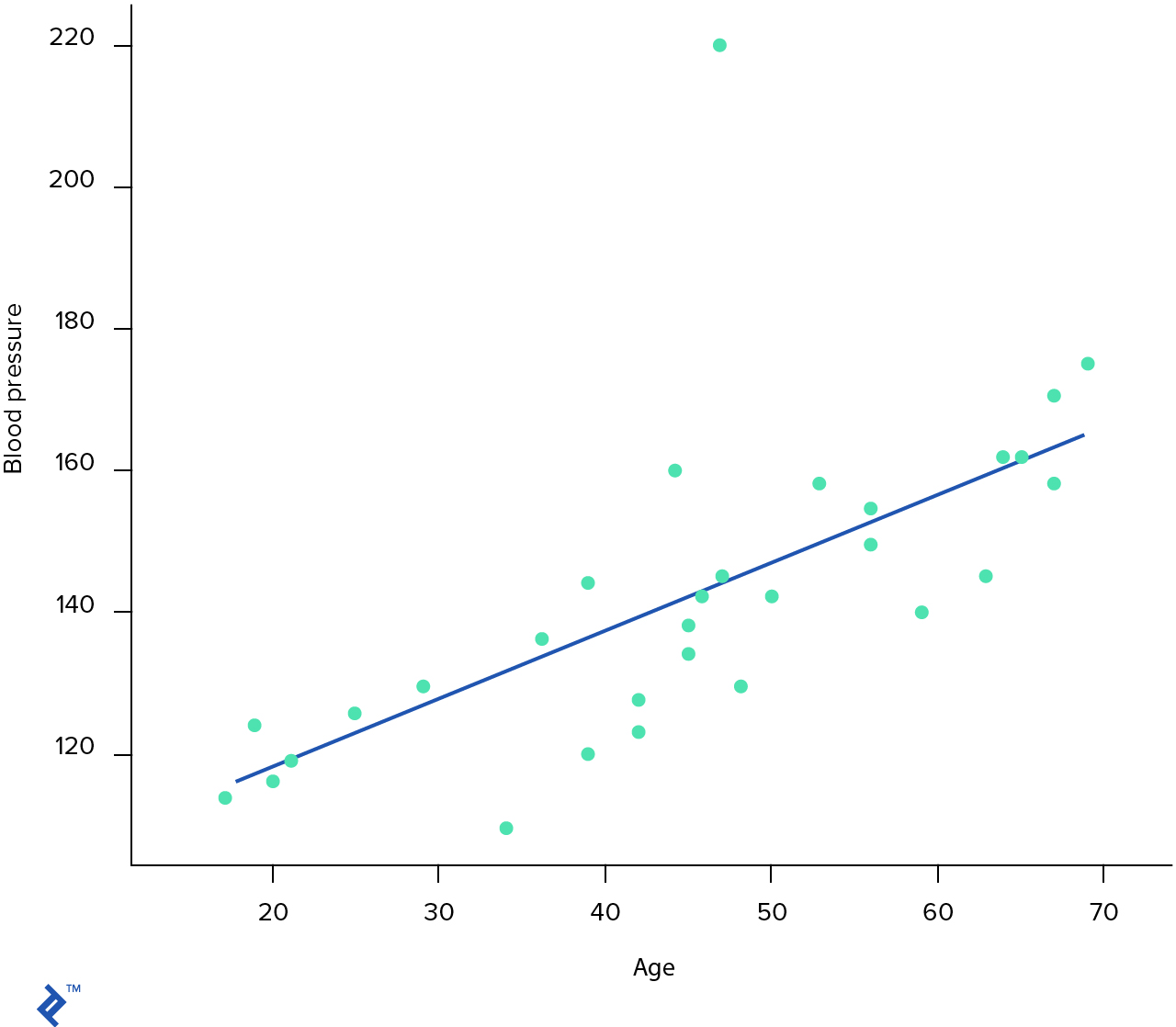
<matplotlib.figure.Figure at 0x120fae1d0>
print( 'Predicted blood pressure at 25 y.o. = ', regr.predict(25) )
print( 'Predicted blood pressure at 45 y.o. = ', regr.predict(45) )
print( 'Predicted blood pressure at 27 y.o. = ', regr.predict(27) )
print( 'Predicted blood pressure at 34.5 y.o. = ', regr.predict(34.5) )
print( 'Predicted blood pressure at 78 y.o. = ', regr.predict(78) )
Predicted blood pressure at 25 y.o. = [[ 122.98647692]]
Predicted blood pressure at 45 y.o. = [[ 142.40388395]]
Predicted blood pressure at 27 y.o. = [[ 124.92821763]]
Predicted blood pressure at 34.5 y.o. = [[ 132.20974526]]
Predicted blood pressure at 78 y.o. = [[ 174.44260555]]
Tipos de Datos Estadísticos
Cuando se trabaja con problemas de aprendizaje de máquina, es importante saber reconocer los diferentes tipos de datos. Se podría tener numéricos (continuos o discretos), categóricos o data ordinal.
Los datos numéricos tienen significado como medida. Por ejemplo: edad, peso, número de bitcoins de una persona o cuantos artículos puede escribir una persona al mes. Los datos numéricos también pueden ser de tipo discreto o continuo.
- Los datos discretos representan data que puede ser contados con números enteros, por ejemplo, la cantidad de cuartos en un apartamento o las veces que gira una moneda.
- Los datos continuos no son necesariamente representados con números enteros. Por ejemplo, si estas midiendo la distancia que puedes saltar, podría ser 2 metros o podría ser 1.5 metros, o quizás 1.652245.
Los datos categóricos representan valores como el sexo de una persona, estado marital, país, etc. Estos datos pueden ser de valor numérico pero esos números no tendrían valor matemático. No puedes sumarlos.
Los datos ordinales puedes ser una mezcla de los otros tipos en donde las categorías podrían ser numeradas de forma matemáticamente significativa. Un ejemplo común son las clasificaciones: A menudo se nos pide que se clasifiquen las cosas en una escala del uno al diez, y en tales casos sólo los números enteros están permitidos. A pesar de que podemos utilizar estos datos numéricamente (por ejemplo, para encontrar la clasificación promedio de algo), a menudo lidiamos con estos datos como si fueran categóricos cuando se va a aplicar métodos de aprendizaje de máquina.
Regresión Logística
Regresión lineal es un increíble algoritmo que nos ayuda a predecir valores numéricos como por ejemplo, el precio de una casa con un tamaño específico y determinados cuartos. Sin embargo, en ocasiones tal vez querríamos predecir datos categóricos para obtener respuestas a preguntas como:
- ¿Es un perro o un gato?
- ¿Este tumor es maligno o benigno?
- ¿Este vino es bueno o malo?
- ¿Este email es spam o no?
O incluso:
- ¿Qué número está en esta foto?
- ¿A qué categoría pertenece este email?
Todas estas preguntas son específicas del problema de clasificación. Y el algoritmo de clasificación más sencillo se llama regresión logística, el cual es eventualmente igual a la regresión lineal excepto que tiene una hipótesis diferente.
Primero que todo podemos reusar la misma hipótesis lineal $h_\theta(x) = \theta^T X$ (esto es de forma vectorizada). Mientras que la regresión lineal podría salir como cualquier número en los intervalos $[a, b]$, la regresión logística solo puede sacar valores en $[−1, 1]$, lo que se refiere a la probabilidad de que el objeto sea de una categoría o no.
Si utilizamos una función sigmoide, podemos convertir cualquier valor numérico para que represente un valor en el intervalo $[−1, 1]$.
\[f(x) = \frac{1}{1 + e^x}\]Ahora, en lugar de $x$, necesitaríamos pasar una hipótesis existente y obtendríamos:
\[f(x) = \frac{1}{1 + e^{\theta_0 + \theta_1 * x_1 + ... + \theta_n * x_n}}\]Luego de esto podemos aplicar un umbral sencillo que diga que, si la hipótesis es mayor a cero, será un valor verdadero de lo contrario será falso.
\[h_\theta(x) = \begin{cases} 1 & \mbox{if } \theta^T X > 0 \\ 0 & \mbox{else} \end{cases}\]Esto significa que podemos usar la misma función de costo y el mismo algoritmo de gradiente descendiente para aprender una hipótesis de regresión logística.
En el próximo ejemplo de aprendizaje de máquina, aconsejaremos a los pilotos del transbordador espacial si deberían o no controlar el aterrizaje de forma manual o automática. Contamos con un set de datos muy pequeño—15 muestras—que consisten en seis características y la verdad del terreno.
En los algoritmos de aprendizaje máquina, el término “verdad del terreno” se refiere a la precisión de la clasificación de los sets de entrenamiento para técnicas de aprendizaje supervisado.
Nuestro set de datos está completo, lo cual significa que no faltan características; a pesar de esto, algunas características tienen un “*” en lugar de la categoría, lo que significa que esta característica no importa. Se reemplazarán todos los asteriscos parecidos a este con ceros.
de sklearn.linear_model importar LogisticRegression
# Data
data_path = os.path.join(os.getcwd(), "data/shuttle-landing-control.csv")
dataset = read_csv(data_path, header=None,
names=['Auto', 'Stability', 'Error', 'Sign', 'Wind', 'Magnitude', 'Visibility'],
na_values='*').fillna(0)
# Preparar características
X = dataset[['Stability', 'Error', 'Sign', 'Wind', 'Magnitude', 'Visibility']]
y = dataset[['Auto']].values.reshape(1, -1)[0]
model = LogisticRegression()
model.fit(X, y)
# Por ahora nos falta un concepto importante. No sabemos qué tan bien funciona nuestro
# modelo y debido a ello, en realidad no podemos mejorar el rendimiento de nuestra hipótesis.
# Hay muchas métricas útiles pero por ahora, validaremos que tan bien
# Actúa nuestro algoritmo en el set de datos, en el cual aprendió.
"La puntuación de nuestro modelo es %2.2f%%" % (model.score(X, y) * 100)
Puntuación de nuestro modelo es 73.33%
¿Validación?
En el ejemplo anterior, validamos el rendimiento de nuestro modelo usando los datos de aprendizaje. Sin embargo, ¿será una buena opción, dado que nuestro algoritmo podría despreciar o no los datos? Veamos un ejemplo más sencillo en donde tenemos una característica que representa el tamaño de una casa, y otra que representa el precio.
de sklearn.pipeline importar make_pipeline
de sklearn.preprocessing importer PolynomialFeatures
de sklearn.linear_model importar LinearRegression
de sklearn.model_selection importar cross_val_score
# Función Verdad del terreno
ground_truth = lambda X: np.cos(15 + np.pi * X)
# Generar observaciones aleatorias alrededor de la función verdad del terreno
n_samples = 15
degrees = [1, 4, 30]
X = np.linspace(-1, 1, n_samples)
y = ground_truth(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
models = {}
# Trazar todos modelos del algoritmo de aprendizaje de máquina
para idx, degree in enumerate(degrees):
ax = plt.subplot(1, len(degrees), idx + 1)
plt.setp(ax, xticks=(), yticks=())
# Definir el modelo
polynomial_features = PolynomialFeatures(degree=degree)
model = make_pipeline(polynomial_features, LinearRegression())
models[degree] = model
# Entrenar el modelo
model.fit(X[:, np.newaxis], y)
# Evaluar el modelo usando validación cruzada
scores = cross_val_score(model, X[:, np.newaxis], y)
X_test = X
plt.plot(X_test, model.predict(X_test[:, np.newaxis]), label="Model")
plt.scatter(X, y, edgecolor='b', s=20, label="Observations")
plt.xlabel("x")
plt.ylabel("y")
plt.ylim((-2, 2))
plt.title("Degree {}\nMSE = {:.2e}".format(
degree, -scores.mean()))
plt.show()
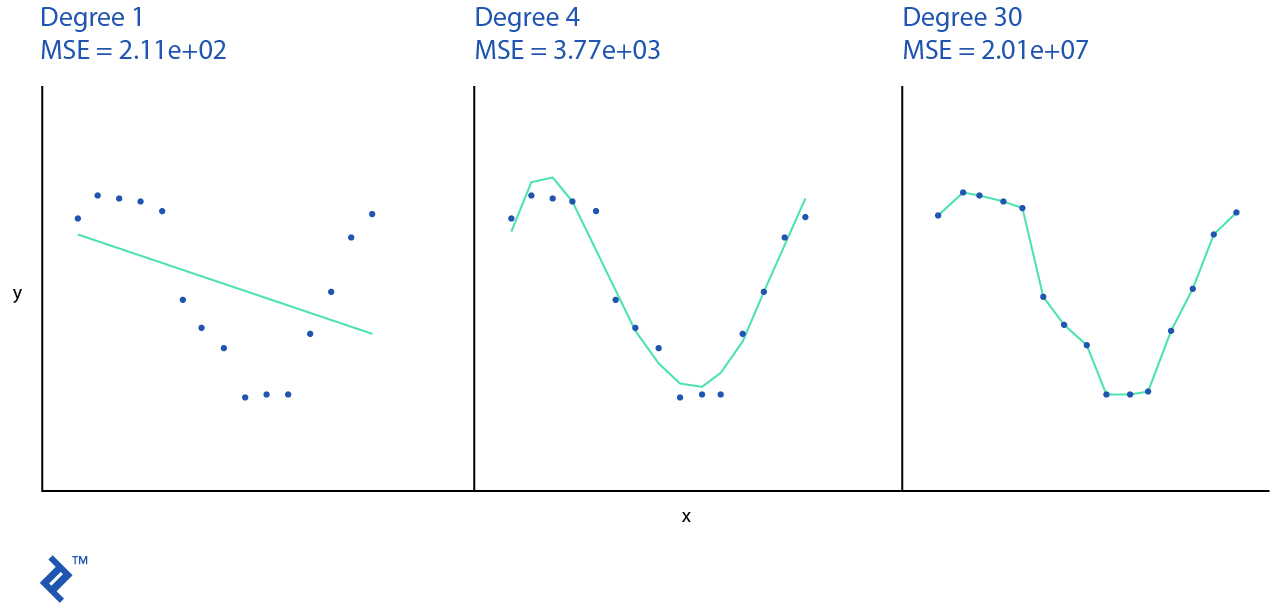
El modelo de algoritmo de aprendizaje de máquina esta sobregeneralizado si no puede generalizar ni los datos de entrenamiento ni nuevas observaciones. En el ejemplo anterior usamos una hipótesis lineal simple, que no representa los datos de entrenamiento reales y tendrá un rendimiento muy bajo. Usualmente, la sobregeneralización no se discute debido a que puede ser detectada fácilmente con buenas mediciones.
Si nuestro algoritmo recuerda cada observación que se le mostró entonces tendrá un bajo rendimiento con nuevas observaciones que estén fuera del set de datos de entrenamiento. A esto se le llama sobreajuste. Por ejemplo, un modelo polinómico de trigesimo grado pasa la mayoría de los puntos y tiene una buena puntuación en el set de entrenamiento pero cualquier otro dato fuera de esto tendrá un mal rendimiento.
Nuestro set de datos consiste de una característica sencilla que se puede trazar en 2D; pero en la vida real, podríamos tener set de datos con cientos de características, lo cual las hace imposible de trazar visualmente en un espacio Euclidiano. ¿Qué otras opciones tenemos para ver si el modelo es sobregeneralizado o sobreajustado?
Es tiempo de presentarte el concepto curva de aprendizaje. Esto se trata de un gráfico simple que traza el error cuadrático sobre el número de muestras de entrenamiento.
En materiales de aprendizaje encontrarás gráficos similares a estos:
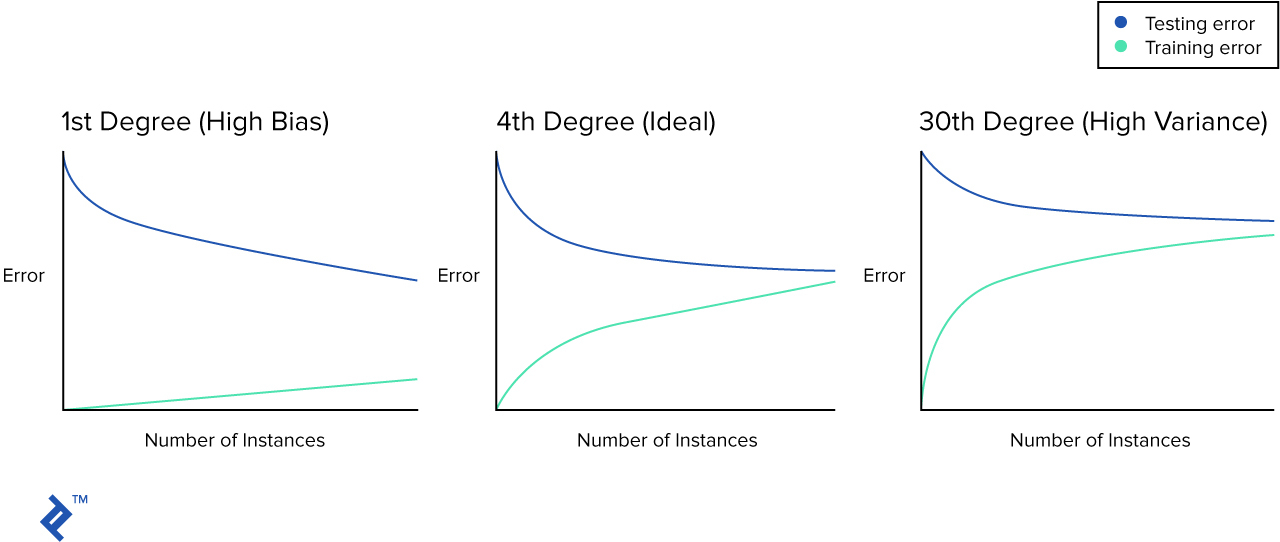
Pero en la vida real puede que no te encuentres con una imagen tan perfecta. Tracemos la curva de aprendizaje para cada uno de nuestros modelos.
from sklearn.model_selection import learning_curve, ShuffleSplit
# Trazar curvas de aprendizaje
plt.figure(figsize=(20, 5))
for idx, degree in enumerate(models):
ax = plt.subplot(1, len(degrees), idx + 1)
plt.title("Degree {}".format(degree))
plt.grid()
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes = np.linspace(.6, 1.0, 6)
# Validación cruzada con 100 iteraciones para obtener una prueba sencilla de *mean* y entrenamiento
# curvas de puntuación cada vez con 20% de los datos seleccionados aleatoriamente como set de validación.
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
model = models[degree]
train_sizes, train_scores, test_scores = learning_curve(
model, X[:, np.newaxis], y, cv=cv, train_sizes=train_sizes, n_jobs=4)
train_scores_mean = np.mean(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Test score")
plt.legend(loc = "best")
plt.show()
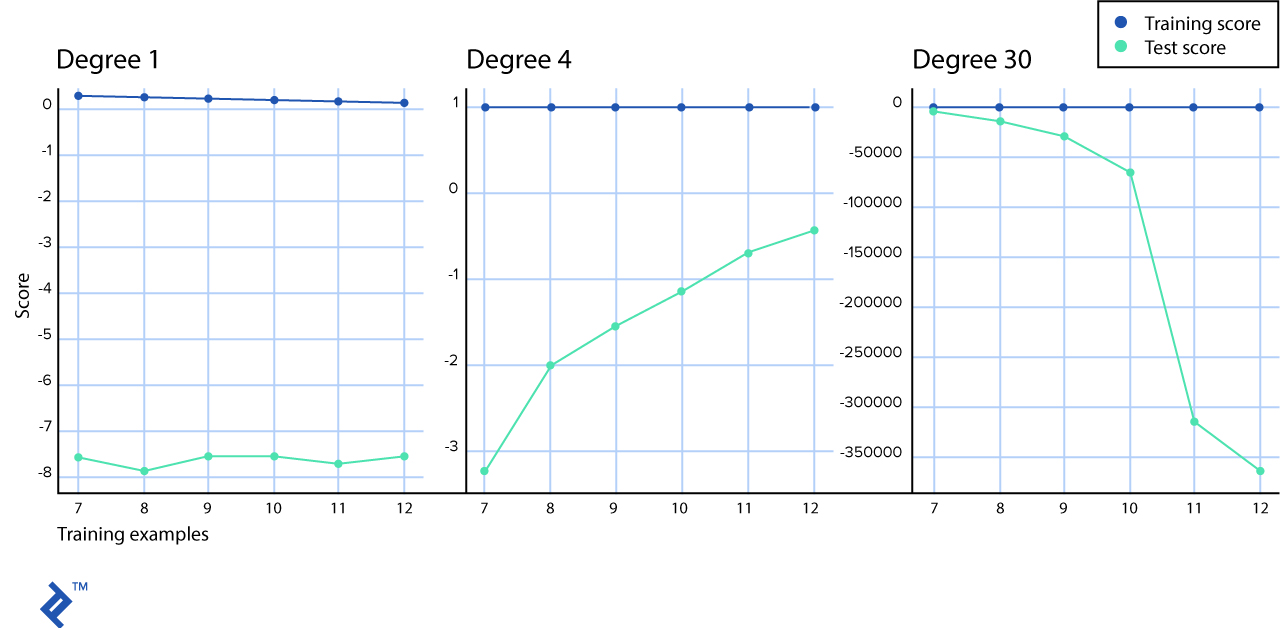
En nuestro escenario simulado, la línea azul que representa la puntuación de entrenamiento, parece una línea recta. En realidad, decrece ligeramente—puedes verlo en el gráfico del polinomio de primer-grado pero en los otros en muy sutil como para verlo con esta resolución. Al menos podemos ver que existe una gran diferencia entre las curvas de aprendizaje de entrenamiento y observaciones de la prueba con un escenario de “gran inclinación”.
En el gráfico de clasificación de aprendizaje “normal” en el medio, se puede observar como las líneas del puntaje de entrenamiento y de prueba se juntan.
Y en el gráfico de “variación alta” se puede ver que con un bajo número de muestras, las puntuaciones de la prueba y el entrenamiento son muy similares, sin embargo, cuando aumentas el número de pruebas, el puntaje de entrenamiento permanece casi perfecto mientras que el de prueba se aleja en aumento.
Podemos arreglar modelos sobregeneralizados (también llamados modelos con gran inclinación) si utilizamos una hipótesis no-lineal, por ejemplo, la hipótesis con más características polinómicas.
Nuestro modelo sobreajustado (gran variacion) para cada ejemplo que se le muestra; pero aun así cuando se le introduce datos de prueba, la diferencia entre curvas de aprendizaje aumenta. Podemos utilizar regularización, validación cruzada y más muestras de datos para arreglar modelos sobreajustados.
Validación cruzada
Una de las prácticas comunes que se utilizan para evitar un sobreajuste se trata de guardar parte de los datos disponibles y utilizarlos como set de prueba. Sin embargo, cuando se evalúan diferentes configuraciones del modelo, como el número de características polinómicas, aún existe riesgo de sobreajustar el set de prueba debido a que los parámetros se pueden cambiar ligeramente para conseguir un rendimiento óptimo del estimador y es por esto que nuestro conocimiento sobre el set de prueba puede fugarse hacia el modelo. Para resolver este problema necesitamos apropiarnos de otra parte del set de datos, al que se le llama “set de validación.” El entrenamiento se realiza en el set entrenamiento y cuando creemos que hemos logrado el rendimiento óptimo del modelo, podemos hacer la evaluación usando el set de validación.
Sin embargo, si hacemos tres sets de particiones de los datos, se reducirá dramáticamente el número de muestras que se pueden usar para entrenar los modelos y los resultados pueden depender en una opción aleatoria particular para el par de sets de validación-entrenamiento.
Una solución a este problema es un procedimiento llamado validación cruzada. En una validación cruzada $k$-fold estándar, se dividen los datos en sub-sets $k$ llamados pliegues. Luego se entrena el algoritmo de forma iterativa con $k-1$ folds, mientras se utilizan los pliegues que restan como sets de prueba (llamados “pliegues holdout”)
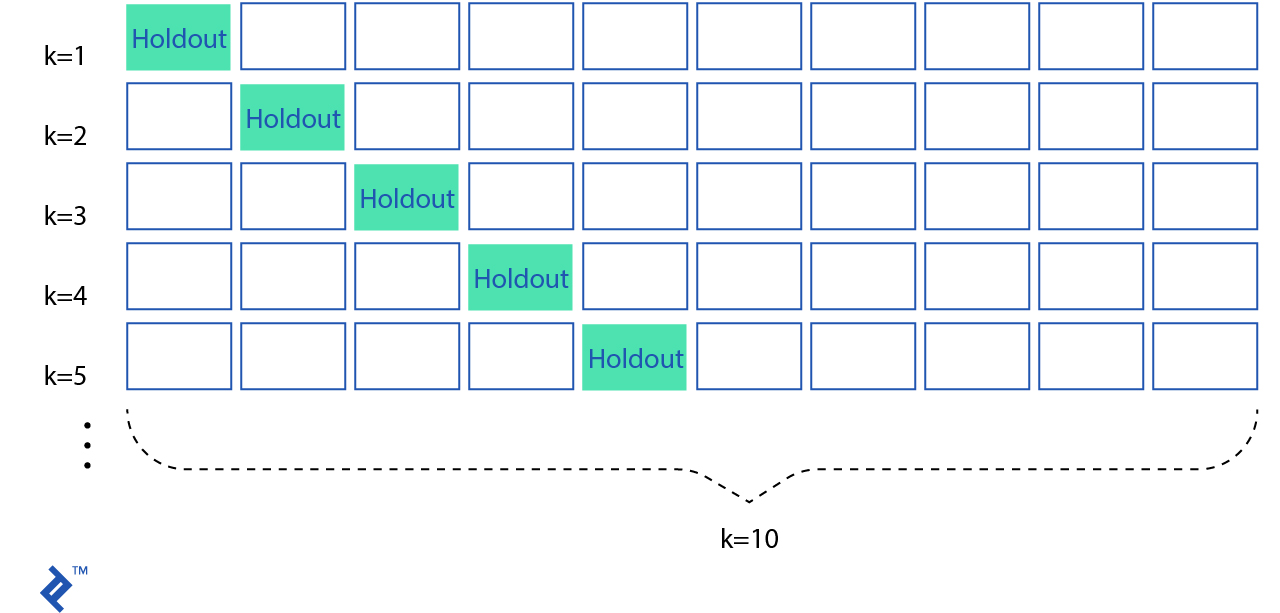
La validación cruzada permite graduar parámetros solamente con el set de entrenamiento original. Esto te permite conservar tu set de prueba como un set de datos invisible para escoger tu modelo final.
Existen muchas otras técnicas de validación cruzada como leave P out, stratified $k$-fold, shuffle and split, etc. pero estas estan fuera del alcance de este artículo.
Regularización
Esta es otra técnica que puede ayudar a resolver el problema de sobreajustamiento del modelo. La mayoría de los sets de datos tienen un patrón y algo de ruido. La meta de la regularización es reducir la influencia del ruido en el modelo.
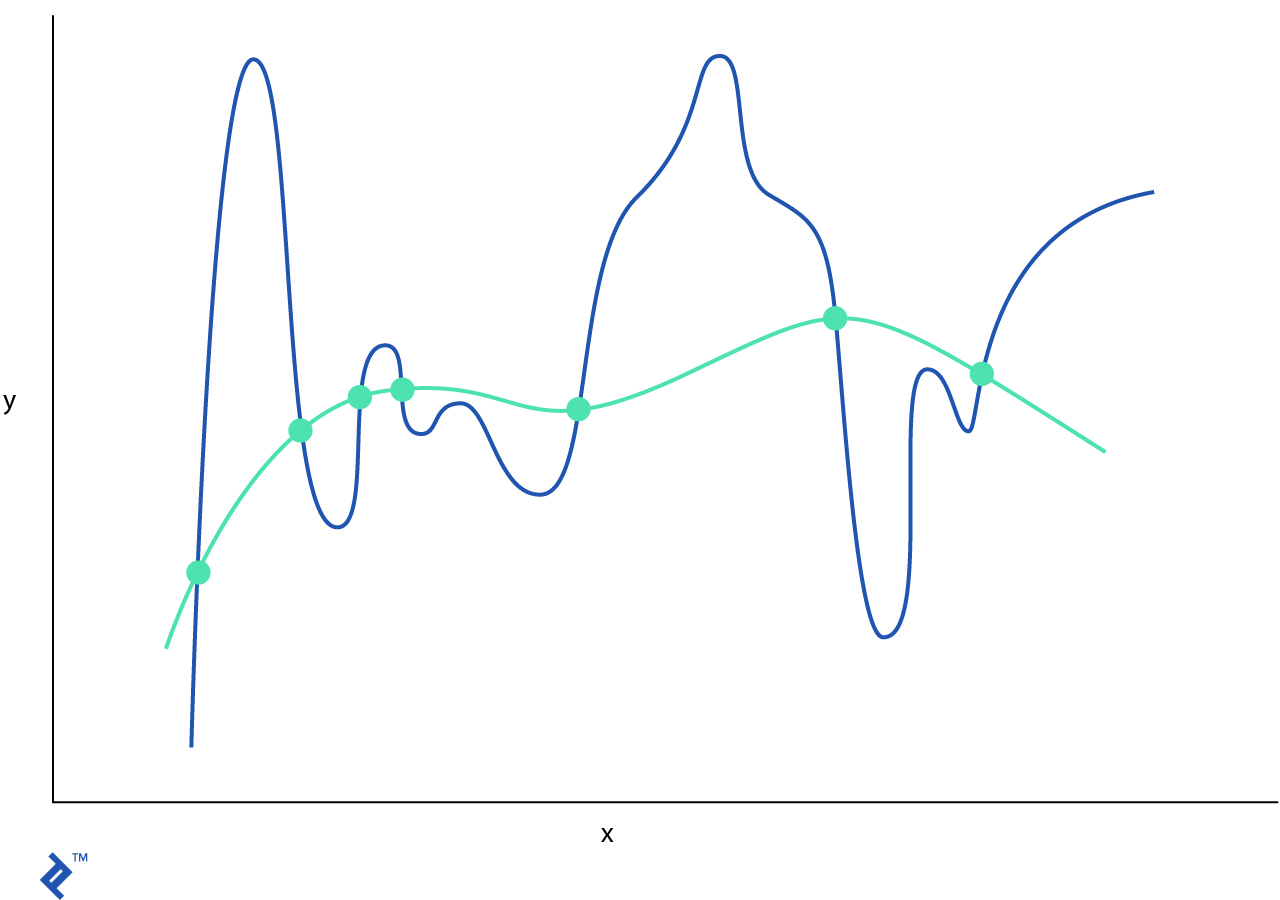
Hay tres técnicas principales de regularización: Lasso, Tikhonov y malla elástica.
Regularización L1 (o Regularización Lasso) es aquella que seleccionará algunas características para minimizar a cero, de manera que estas no tendrán nada que ver con el modelo final. La L1 puede ser vista como un método para seleccionar características importantes.
** Regularización L2** (o ** Regularización Tikhonov**) es la que se encargará de forzar todas las características a que sean relativamente pequeñas, para que así sean de menor influencia para el modelo.
Malla elástica es la combinación de L1 y L2.
Normalización (Característica de escalado)
Característica de escalado se trata también de un paso importante mientras se pre-procesan los datos. Nuestro set de datos puede tener algunas características con valores $[-\infty, \infty]$ y otras características con diferentes escalas. Este es un método que permite estandarizar los rangos de valores independientes.
Característica de escalado es un proceso importante para mejorar el rendimiento de los modelos de aprendizaje. Primero que todo el descenso por gradiente convergerá mucho más rápido si todas las características están escaladas a la misma pauta. De igual forma, muchos de los algoritmos—por ejemplo: máquinas de vectores de soporte (SVM)—funcionan al calcular la distancia entre dos puntos y si una de las características tiene valores grandes, entonces la distancia será influenciada de gran manera por esta característica.
Máquinas de Vectores de Soporte
SVM (por su nombre en inglés Support Vector Machines) es otro popular algoritmo de aprendizaje de máquina que puede ser usado para clasificación y problemas de regresión. En SVM se traza cada observación como un punto en un espacio dimensional $n$- donde $n$ es el número de características que tenemos. El valor de cada característica es el valor de coordenadas particulares. Luego se intenta encontrar un hiper-plano que separe muy bien dos clases.
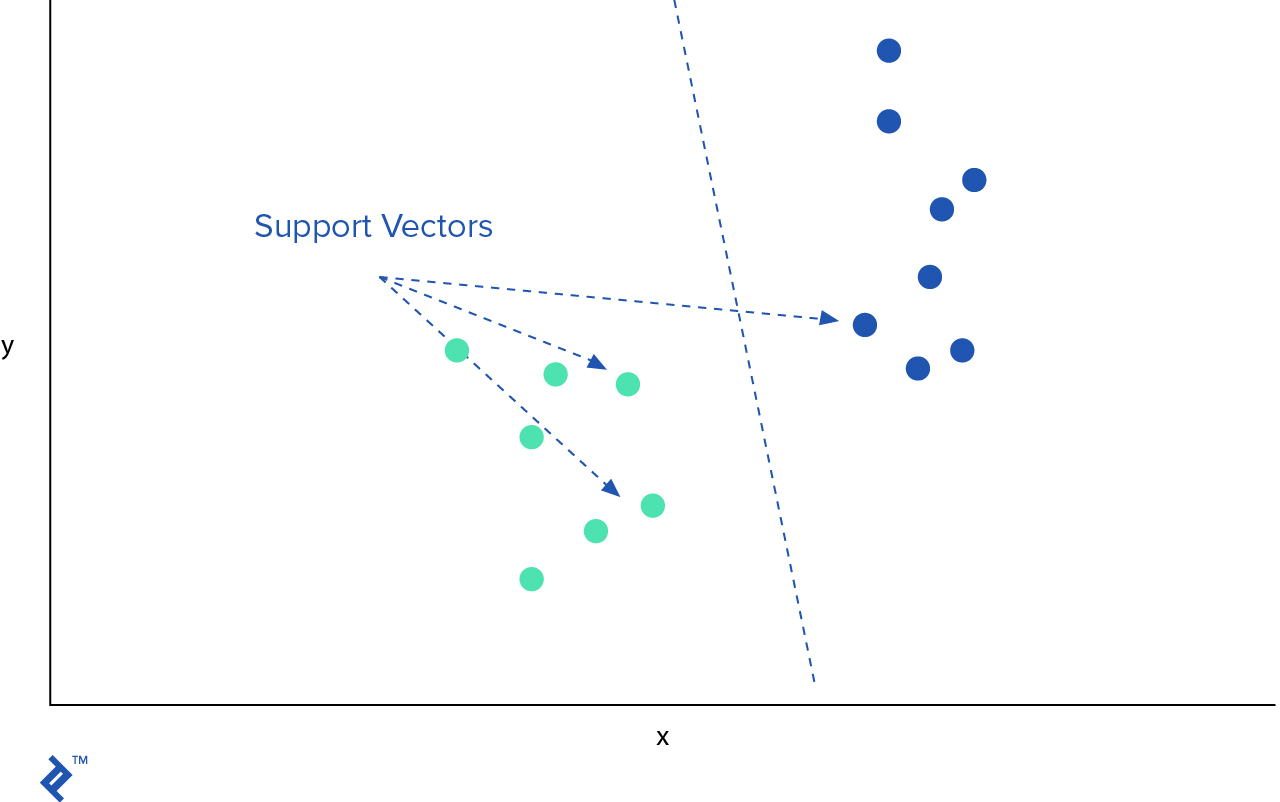
Después de identificar el mejor hiper-plano, querremos agregar márgenes que ayudarían a separar más aún las dos clases.
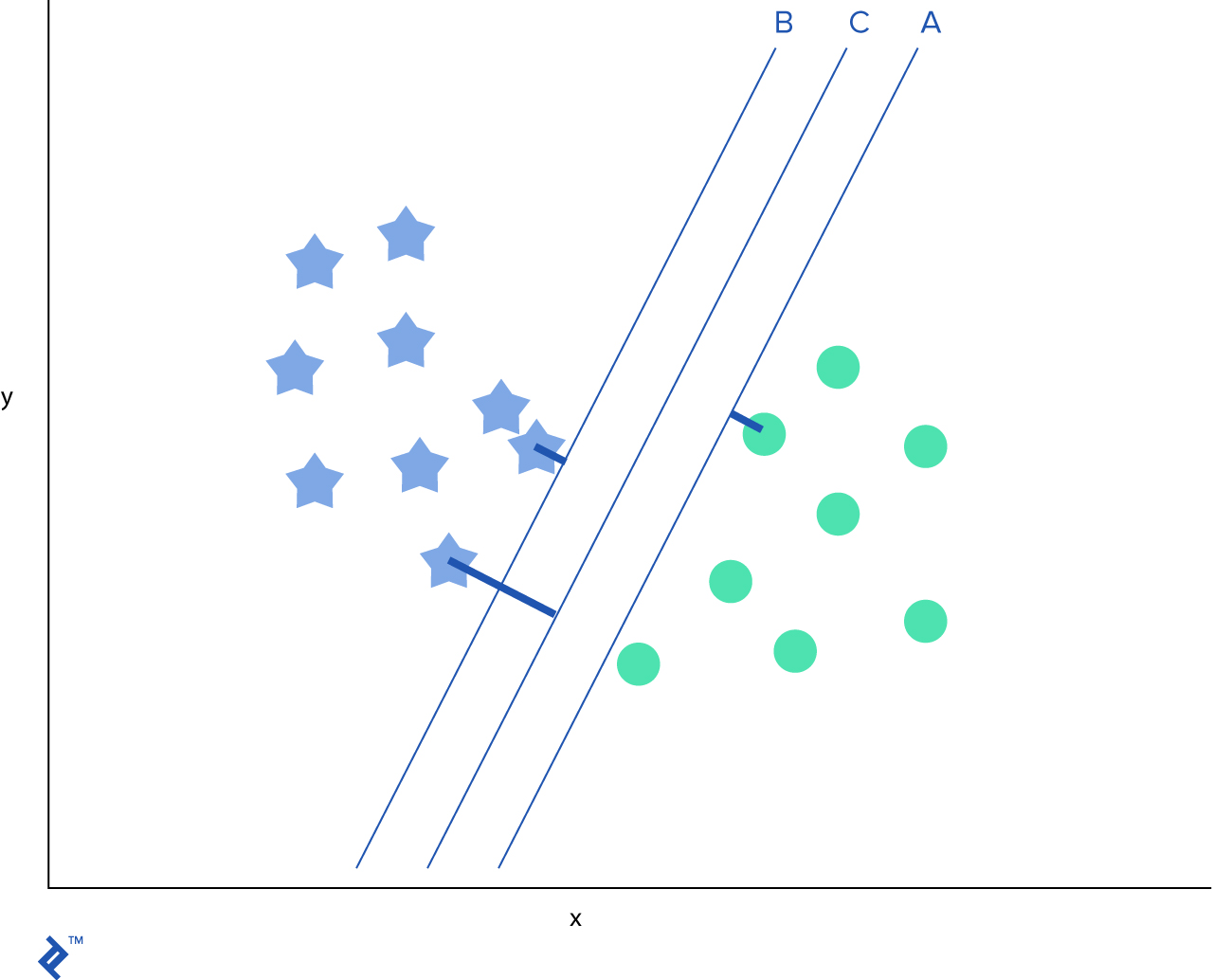
SVM es muy efectivo cuando el número de características es muy alto o si el número de características es más mayor al número de muestras de datos. Aunque, debido a que SVM funciona normalmente con vectores, es crucial normalizar los datos antes de usarlos.
Redes Neuronales
Probablemente los algoritmos de red neural son la rama más emocionante de los estudios de aprendizaje de máquina. Las redes neuronales tratan de imitar la conexión de las neuronas en el cerebro.
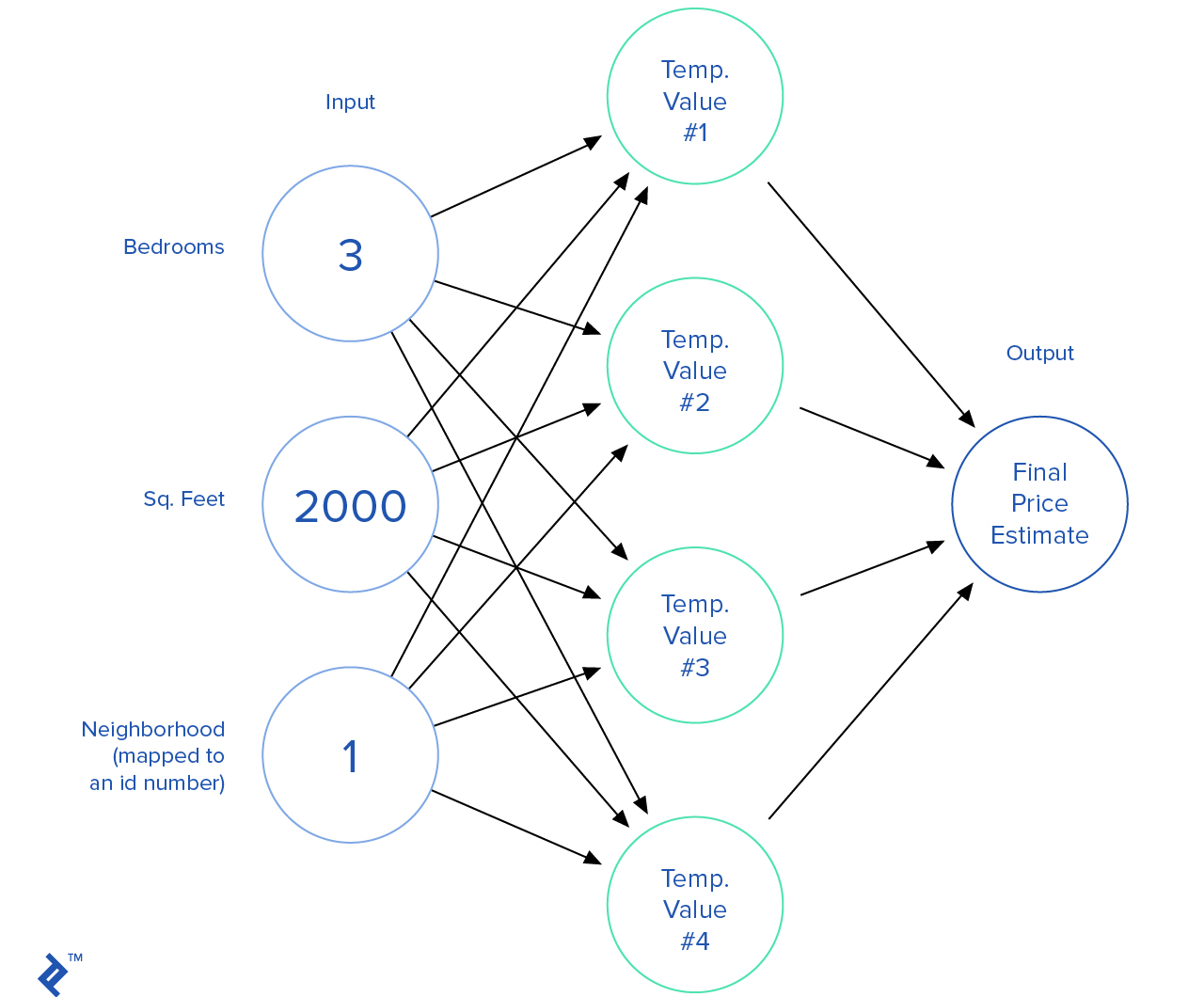
Así es como se va una red neuronal. Combinamos muchos nodos donde cada nodo toma un conjunto de salidas, hace algunas calculaciones y luego saca un valor.
Hay una gran variedad de algoritmos de redes neuronales tanto para aprendizaje supervisado como para no-supervisado. Las redes neuronales pueden ser usadas para manejar carros autónomos, jugar videojuegos, aterrizar aviones, clasificar imágenes y más.
El Infame Titanic
El RMS Titanic fue un barco británico que se hundió en el Océano Atlántico del norte el 15 de Abril de 1912 después de colisionar con un iceberg. Habían abordo alrededor de 2,224 pasajeros y tripulantes, de los cuales murieron más de 1,500, lo que lo convirtió en uno de los desastres marítimos comerciales más mortífero en los últimos tiempos.
Ahora que entendemos la intuición de uno de los algoritmos más básicos del aprendizaje de máquinas usado para clasificación de problemas, podemos aplicar nuestro conocimiento para predecir la tasa supervivencia de aquellos a bordo del Titanic.
Nuestro set de datos vendrá de la plataforma de datos científicos de competitividad de Kaggle.
import os
from pandas import read_csv, concat
# Cargar datos
data_path = os.path.join(os.getcwd(), "data/titanic.csv")
dataset = read_csv(data_path, skipinitialspace=True)
dataset.head(5)
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
Nuestro primer paso será cargar y explorar los datos. Tenemos 891 registros de prueba; cada registro tiene la siguiente estructura:
- passengerId – ID del pasajero abordo
- survival – Sí la persona sobrevivió o no el accidente
- pclase – Tipo de Ticket, e.g., 1ra, 2da, 3ra
- gender – Género del pasajero: Masculino o femenino
- name – Título incluído
- age – Edad en anos
- sibsp – Número de parientes/cónyuges abordo del Titanic
- parch – Número de padres/hijos abordo del Titanic
- ticket – Número Ticket
- fare – Costo pasaje
- cabin – Número cabina
- embarked – Puerto de embarcación
Este set de datos contiene información numérica y categórica. Usualmente es una buena idea indagar aún más en los datos que se tienen, y basándose en ellos crear suposiciones. Sin embargo, en este caso nos saltaremos este paso e iremos directo a las predicciones.
import pandas as pd
# Necesitamos eliminar algunas características insignificantes y mapear el resto.
# Número y costo del boleto no deberían contribuir en el rendimiento de nuestro modelo.
# Característica de nombres viene con títulos (como: Sr. Srta. Doctor) incluidos.
# El género es muy importante.
# El Puerto de embarcación podría ser atribuir algún valor.
# Usar el Puerto de embarcación podría ser contra-intuitivo pero podría
# existir una tasa de supervivencia más alta para pasajeros que abordaron en el mismo Puerto.
dataset['Title'] = dataset.Name.str.extract(' ([A-Za-z]+)\.', expand=False)
dataset = dataset.drop(['PassengerId', 'Ticket', 'Cabin', 'Name'], axis=1)
pd.crosstab(dataset['Title'], dataset['Sex'])
| Title \ Sex | female | male |
| Capt | 0 | 1 |
| Col | 0 | 2 |
| Countess | 1 | 0 |
| Don | 0 | 1 |
| Dr | 1 | 6 |
| Jonkheer | 0 | 1 |
| Lady | 1 | 0 |
| Major | 0 | 2 |
| Master | 0 | 40 |
| Miss | 182 | 0 |
| Mlle | 2 | 0 |
| Mme | 1 | 0 |
| Mr | 0 | 517 |
| Mrs | 125 | 0 |
| Ms | 1 | 0 |
| Rev | 0 | 6 |
| Sir | 0 | 1 |
# Reemplazaremos muchos títulos con un nombre más común, equivalente Inglés,
# o re-clasificación
dataset['Title'] = dataset['Title'].replace(['Lady', 'Countess','Capt', 'Col',\
'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Other')
dataset['Title'] = dataset['Title'].replace('Mlle', 'Miss')
dataset['Title'] = dataset['Title'].replace('Ms', 'Miss')
dataset['Title'] = dataset['Title'].replace('Mme', 'Mrs')
dataset[['Title', 'Survived']].groupby(['Title'], as_index=False).mean()
| Title | Survived | |
| 0 | Master | 0.575000 |
| 1 | Miss | 0.702703 |
| 2 | Mr | 0.156673 |
| 3 | Mrs | 0.793651 |
| 4 | Other | 0.347826 |
# Ahora mapearemos categorias alfanumericas a números
title_mapping = { 'Mr': 1, 'Miss': 2, 'Mrs': 3, 'Master': 4, 'Other': 5 }
gender_mapping = { 'female': 1, 'male': 0 }
port_mapping = { 'S': 0, 'C': 1, 'Q': 2 }
# Mapa de título
dataset['Title'] = dataset['Title'].map(title_mapping).astype(int)
# Mapa de género
dataset['Sex'] = dataset['Sex'].map(gender_mapping).astype(int)
# Mapa de puerto
freq_port = dataset.Embarked.dropna().mode()[0]
dataset['Embarked'] = dataset['Embarked'].fillna(freq_port)
dataset['Embarked'] = dataset['Embarked'].map(port_mapping).astype(int)
# Arreglar errores de edades que falten
dataset['Age'] = dataset['Age'].fillna(dataset['Age'].dropna().median())
dataset.head()
| Survived | Pclass | Sex | Age | SibSp | Parch | Fare | Embarked | Title | |
| 0 | 0 | 3 | 0 | 22.0 | 1 | 0 | 7.2500 | 0 | 1 |
| 1 | 1 | 1 | 1 | 38.0 | 1 | 0 | 71.2833 | 1 | 3 |
| 2 | 1 | 3 | 1 | 26.0 | 0 | 0 | 7.9250 | 0 | 2 |
| 3 | 1 | 1 | 1 | 35.0 | 1 | 0 | 53.1000 | 0 | 3 |
| 4 | 0 | 3 | 0 | 35.0 | 0 | 0 | 8.0500 | 0 | 1 |
En este momento clasificaremos diferentes tipos de algoritmos de aprendizaje de máquina en Python usando scikit-learn para crear un set de modelos diferente. Será fácil ver cual tiene mejor rendimiento.
- Regresión logística con polinomios de números variantes
- Máquina de vectores de soporte con un núcleo lineal
- Máquina de vectores de soporte con un núcleo polinómico
- Red neuronal
Para cada uno de los modelos, usaremos la validación $k$-fold.
de sklearn.model_selection importar KFold, train_test_split
de sklearn.pipeline importar make_pipeline
de sklearn.preprocessing importar PolynomialFeatures, StandardScaler
de sklearn.neural_network importar MLPClassifier
de sklearn.svm importar SVC
# Preparar data
X = dataset.drop(['Survived'], axis = 1).values
y = dataset[['Survived']].values
X = StandardScaler().fit_transform(X)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state = None)
# Prepare cross-validation (cv)
cv = KFold(n_splits = 5, random_state = None)
# Rendimiento
p_score = lambda model, score: print('Performance of the %s model is %0.2f%%' % (model, score * 100))
# Clasificadores
names = [
"Logistic Regression", "Logistic Regression with Polynomial Hypotheses",
"Linear SVM", "RBF SVM", "Neural Net",
]
classifiers = [
LogisticRegression(),
make_pipeline(PolynomialFeatures(3), LogisticRegression()),
SVC(kernel="linear", C=0.025),
SVC(gamma=2, C=1),
MLPClassifier(alpha=1),
]
# iterate over classifiers
models = []
trained_classifiers = []
for name, clf in zip(names, classifiers):
scores = []
for train_indices, test_indices in cv.split(X):
clf.fit(X[train_indices], y[train_indices].ravel())
scores.append( clf.score(X_test, y_test.ravel()) )
min_score = min(scores)
max_score = max(scores)
avg_score = sum(scores) / len(scores)
trained_classifiers.append(clf)
models.append((name, min_score, max_score, avg_score))
fin_models = pd.DataFrame(models, columns = ['Name', 'Min Score', 'Max Score', 'Mean Score'])
fin_models.sort_values(['Mean Score']).head()
| Name | Min Score | Max Score | Mean Score | |
| 2 | Linear SVM | 0.793296 | 0.821229 | 0.803352 |
| 0 | Logistic Regression | 0.826816 | 0.860335 | 0.846927 |
| 4 | Neural Net | 0.826816 | 0.860335 | 0.849162 |
| 1 | Logistic Regression with Polynomial Hypotheses | 0.854749 | 0.882682 | 0.869274 |
| 3 | RBF SVM | 0.843575 | 0.888268 | 0.869274 |
Bien, nuestra investigación experimental nos dice que el clasificador SVM tiene el mejor rendimiento con un núcleo de función básica radial (RBF). Ahora podemos serializar nuestro modelo y re-usarlo en aplicaciones de producción.
import pickle
svm_model = trained_classifiers[3]
data_path = os.path.join(os.getcwd(), "best-titanic-model.pkl")
pickle.dump(svm_model, open(data_path, 'wb'))
El aprendizaje de máquina no es complicado, pero es un campo de estudio muy amplio, y requiere conocimiento en el campo de las matemáticas y estadísticas para poder comprender todos sus conceptos.
En este momento el aprendizaje de máquina y el aprendizaje profundo están entre los temas de discusión más buscados de Silicon Valley, principalmente porque pueden automatizar muchas tareas de repetición como reconocimiento de voz, conducir automóviles, comercio financiero, cuidado de pacientes, cocinar, marketing, entre muchos otros.
Ahora con este conocimiento puedes ir y resolver desafíos en Kaggle.
Esto fue una breve introducción al algoritmo de aprendizaje de máquina supervisado. Por suerte existen muchos cursos en línea e información sobre algoritmos de aprendizaje de máquina. Personalmente recomiendo empezar con el curso de Andrew Ng en Coursera.
Fuentes
- Curso Andrew Ng en Coursera
- Kaggle datasets
- Lista de lectura sobre Aprendizaje profundo
- Lista de libros gratis sobre algoritmos de aprendizaje de máquina, minería de datos, aprendizaje profundo y temas relacionados
- An Introduction to Machine Learning Theory and Its Applications: A Visual Tutorial with Examples
About the author
Vlad is a versatile software engineer with experience in many fields. He is currently perfecting his Scala and machine learning skills.

