How to Approach Machine Learning Problems
How do you approach machine learning problems? Are neural networks the answer to nearly every challenge you may encounter?
In this article, Toptal Freelance Python Developer Peter Hussami explains the basic approach to machine learning problems and points out where neural may fall short.
How do you approach machine learning problems? Are neural networks the answer to nearly every challenge you may encounter?
In this article, Toptal Freelance Python Developer Peter Hussami explains the basic approach to machine learning problems and points out where neural may fall short.
Peter’s rare math-modeling expertise includes audio and sensor analysis, ID verification, NPL, scheduling, routing, and credit scoring.
Expertise
PREVIOUSLY AT

One of the main tasks of computers is to automate human tasks. Some of these tasks are simple and repetitive, such as “move X from A to B.” It gets far more interesting when the computer has to make decisions about problems that are far more difficult to formalize. That is where we start to encounter basic machine learning problems.

Historically, such algorithms were built by scientists or experts that had intimate knowledge of their field and were largely based on rules. With the explosion of computing power and the availability of large and diverse data sets, the focus has shifted toward a more computational approach.
Most popularized machine learning concepts these days have to do with neural networks, and in my experience, this created the impression in many people that neural networks are some kind of a miracle weapon for all inference problems. Actually, this is quite far from the truth. In the eyes of the statistician, they form one class of inference approaches with their associated strengths and weaknesses, and it completely depends on the problem whether neural networks are going to be the best solution or not.
Quite often, there are better approaches.
In this article, we will outline a structure for attacking machine learning problems. There is no scope for going into too much detail about specific machine learning models, but if this article generates interest, subsequent articles could offer detailed solutions for some interesting machine learning problems.
First, however, let us spend some effort showing why you should be more circumspect than to automatically think “neural network” when faced with a machine learning problem.
Pros and Cons of Neural Networks
With neural networks, the inference is done through a weighted “network.” The weights are calibrated during the so-called “learning” process, and then, subsequently, applied to assign outcomes to inputs.
As simple as this may sound, all the weights are parameters to the calibrated network, and usually, that means too many parameters for a human to make sense of.
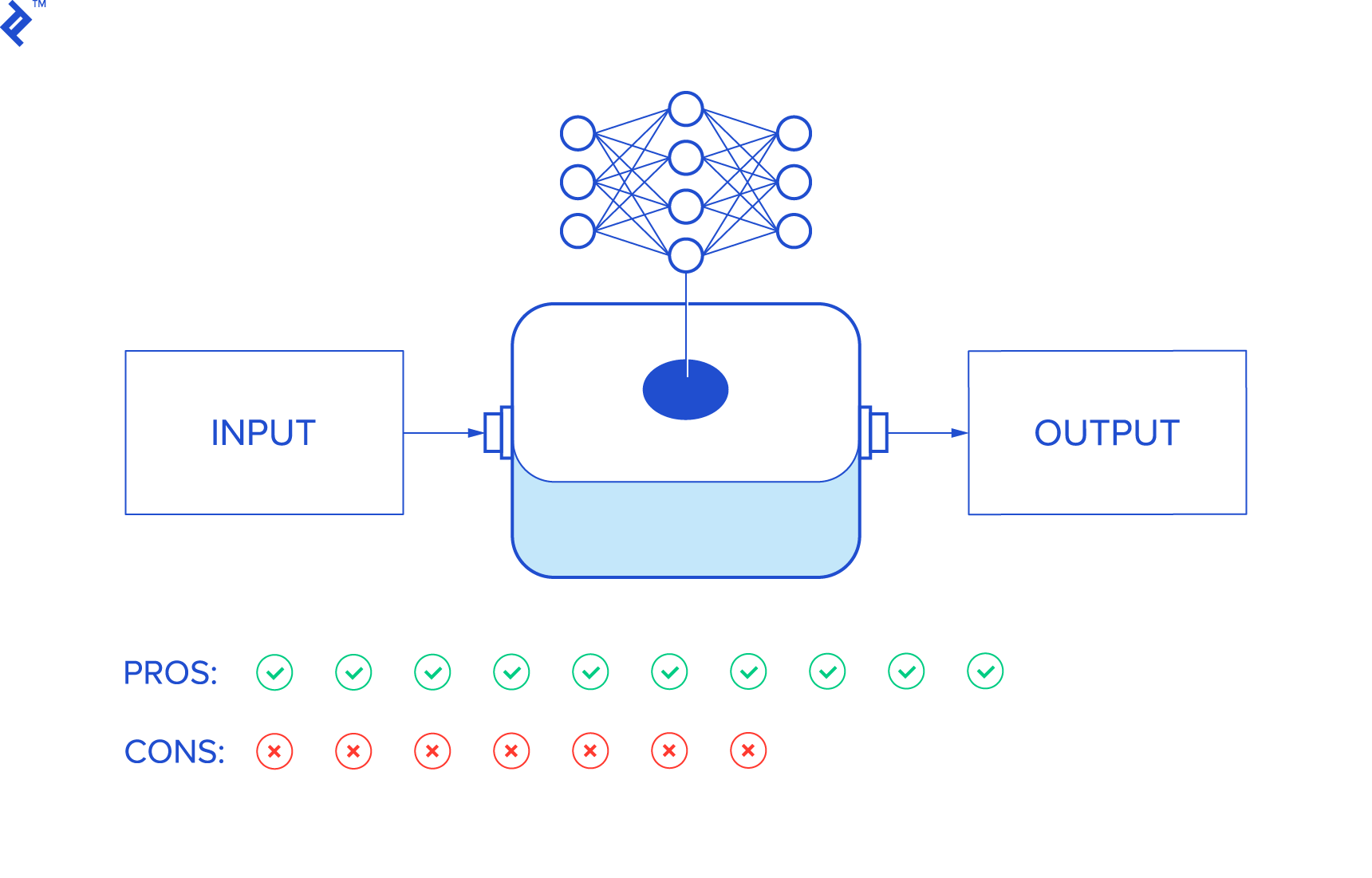
So we might as well just consider neural networks as some kind of an inference black box that connects the input to output, with no specific model in between.
Let us take a closer look at the pros and cons of this approach.
Advantages of Neural Networks
- The input is the data itself. Usable results even with little or no feature engineering.
- Trainable skill. With no feature engineering, there is no need for such hard-to-develop skills as intuition or domain expertise. Standard tools are available for generic inferences.
- Accuracy improves with the quantity of data. The more inputs it sees, the better a neural network performs.
- May outperform classical models when there is not full information about the model. Think of public sentiment, for one.
- Open-ended inference can discover unknown patterns. If you use a model and leave a consideration out of it, it will not detect the corresponding phenomenon. Neural networks might.
Successful neural network example: Google’s AI found a planet orbiting a distant star—where NASA did not—by analyzing accumulated telescope data.
Disadvantages of Neural Networks
- They require a lot of (annotated!) data. First, this amount of data is not always available. Convergence is slow. A solid model (say, in physics) can be calibrated after a few observations—with neural networks, this is out of the question. Annotation is a lot of work, not to mention that it, in itself, is not foolproof.
- No information about the inner structure of the data. Are you interested in what the inference is based on? No luck here. There are situations where manually adjusting the data improves inference by a leap, but a neural network will not be able to help with that.
- Overfitting issues. It happens often that the network has more parameters than the data justifies, which leads to suboptimal inference.
- Performance depends on information. If there is full information about a problem, a solid model tends to outperform a neural network.
- There are sampling problems. Sampling is always a delicate issue, but with a model, one can quickly develop a notion of problematic sampling. Neural networks learn only from the data, so if they get biased data, they will have biased conclusions.
An example of failure: A personal relation told me of a major corporation (that I cannot name) that was working on detecting military vehicles on aerial photos. They had images where there were such vehicles and others that did not. Most images of the former class were taken on a rainy day, while the latter were taken in sunny weather. As a result, the system learned to distinguish light from shadow.
To sum up, neural networks form one class of inference methods that have their pros and cons.
The fact that their popularity outshines all other statistical methods in the eyes of the public has likely more to do with corporate governance than anything else.
Training people to use standard tools and standardized neural network methods is a far more predictable process than hunting for domain experts and artists from various fields. This, however, does not change the fact that using a neural network for a simple, well-defined problem is really just shooting a sparrow with a cannon: It needs a lot of data, requires a lot of annotation work, and in return might just underperform when compared to a solid model. Not the best package.
Still, there is huge power in the fact that they “democratize” statistical knowledge. Once a neural network-based inference solution is viewed as a mere programming tool, it may help even those who don’t feel comfortable with complex algorithms. So, inevitably, a lot of things are now built that would otherwise not exist if we could only operate with sophisticated models.
Approaching Machine Learning Problems
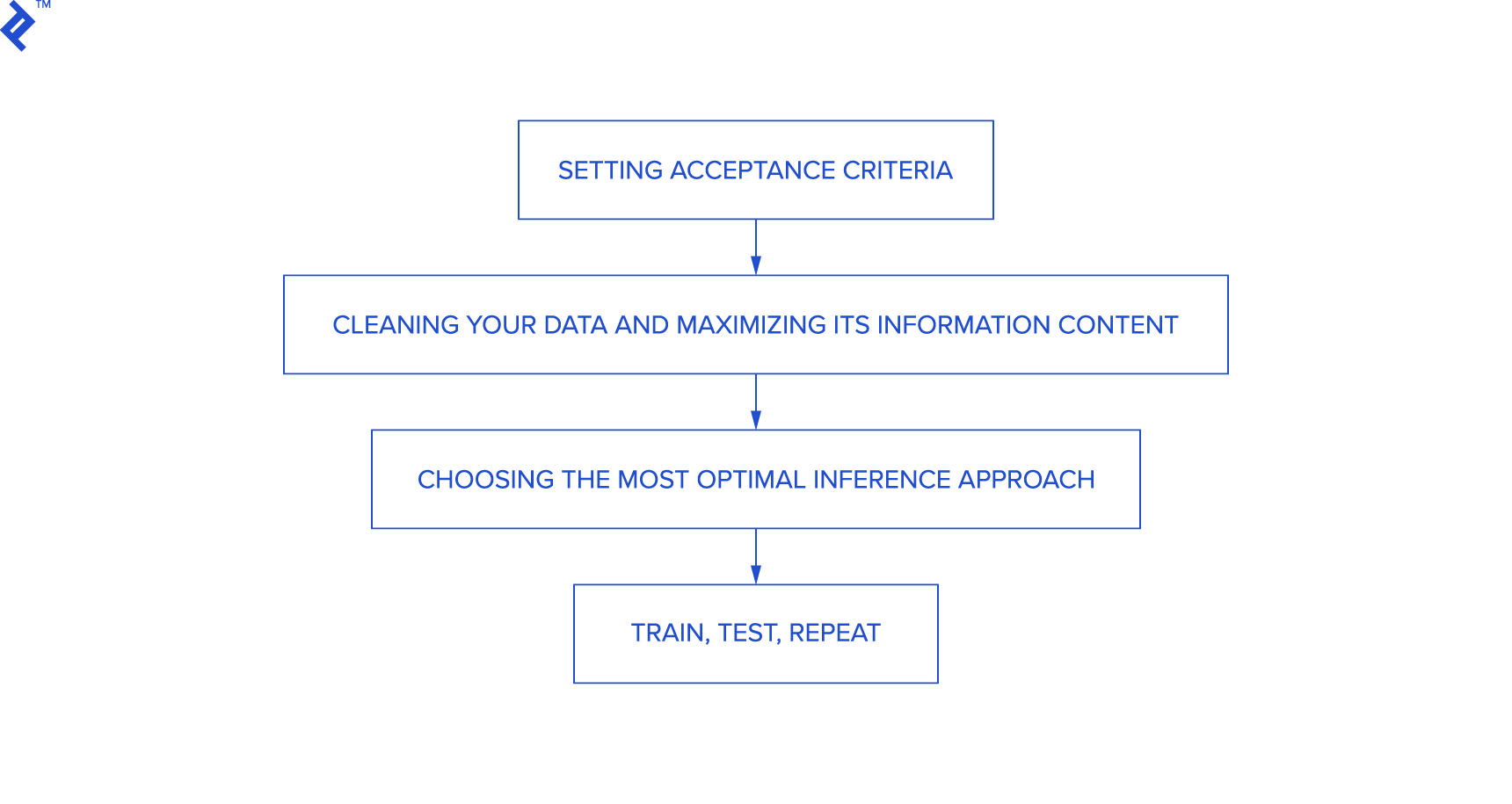
When approaching machine learning problems, these are the steps you will need to go through:
- Setting acceptance criteria
- Cleaning your data and maximizing ist information content
- Choosing the most optimal inference approach
- Train, test, repeat
Let us see these items in detail.
Setting Acceptance Criteria
You should have an idea of your target accuracy as soon as possible, to the extent possible. This is going to be the target you work towards.
Cleansing Your Data and Maximizing Its Information Content
This is the most critical step. First of all, your data should have no (or few) errors. Cleansing it of these is an essential first step. Substitute missing values, try to identify patterns that are obviously bogus, eliminate duplicates and any other anomaly you might notice.
As for information, if your data is very informative (in the linear sense), then practically any inference method will give you good results. If the required information is not in there, then the result will be noise. Maximizing the information means primarily finding any useful non-linear relationships in the data and linearizing them. If that improves the inputs significantly, great. If not, then more variables might need to be added. If all of this does not yield fruit, target accuracy may suffer.
With some luck, there will be single variables that are useful. You can identify useful variables if you—for instance—plot them against the learning target variable(s) and find the plot to be function-like (i.e., narrow range in the input corresponds to narrow range in the output). This variable can then be linearized—for example, if it plots as a parabola, subtract some values and take the square root.
For variables that are noisy—narrow range in input corresponds to a broad range in the output—we may try combining them with other variables.
To have an idea of the accuracy, you may want to measure conditional class probabilities for each of your variables (for classification problems) or to apply some very simple form of regression, such as linear regression (for prediction problems). If the information content of the input improves, then so will your inference, and you simply don’t want to waste too much time at this stage calibrating a model when the data is not yet ready. So keep testing as simple as possible.
Choosing the Most Optimal Inference Approach
Once your data is in decent shape, you can go for the inference method (the data might still be polished later, if necessary).
Should you use a model? Well, if you have good reason to believe that you can build a good model for the task, then you probably should. If you don’t think so, but there is ample data with good annotations, then you may go hands-free with a neural network. In practical machine learning applications, however, there is often not enough data for that.
Playing accuracy vs. cover often pays off tremendously. Hybrid approaches are usually completely fine. Suppose the data is such that you can get near-100% accuracy on 80% of it with a simple model? This means you can demonstrable results quickly, and if your system can identify when it’s operating on the 80% friendly territory, then you’ve basically covered most of the problem. Your client may not yet be fully happy, but this will earn you their trust quickly. And there is nothing to prevent you from doing something similar on the remaining data: with reasonable effort now you cover, say, 92% of the data with 97% accuracy. True, on the rest of the data, it’s a coin flip, but you already produced something useful.
For most practical applications, this is very useful. Say, you’re in the lending business and want to decide whom to give a loan, and all you know is that on 70% of the clients your algorithm is very accurate. Great—true, the other 30% of your applicants will require more processing, but 70% can be fully automated. Or: suppose you’re trying to automate operator work for call centers, you can do a good (quick and dirty) job on the most simple tasks only, but these tasks cover 50% of the calls? Great, the call center saves money if they can automate 50% of their calls reliably.
To sum up: If the data is not informative enough, or the problem is too complex to handle in its entirety, think outside the box. Identify useful and easy-to-solve sub-problems until you have a better idea.
Once you have your system ready, learn, test and loop it until you’re happy with the results.
Train, Test, Repeat
After the previous steps, little of interest is left. You have the data, you have the machine learning method, so it’s time to extract parameters via learning and then test the inference on the test set. Literature suggests 70% of the records should be used for training, and 30% for testing.
If you’re happy with the results, the task is finished. But, more likely, you developed some new ideas during the procedure, and these could help you notch up in accuracy. Perhaps you need more data? Or just more data cleansing? Or another model? Either way, chances are you’ll be busy for quite a while.
So, good luck and enjoy the work ahead!
Further Reading on the Toptal Blog:
Understanding the basics
Machine learning vs. deep learning: What's the difference?
Machine learning includes all inference techniques while deep learning aims at uncovering meaningful non-linear relationships in the data. So deep learning is a subset of machine learning and also a means of automated feature engineering applied to a machine learning problem.
Which language is best for machine learning?
The ideal choice is a language that has both broad programming library support and allows you to focus on the math rather than infrastructure. The most popular language is Python, but algorithmic languages such as Matlab or R or mainstreamers like C++ and Java are all valid choices as well.
Machine learning vs. neural networks: What's the difference?
Neural networks represent just one approach within machine learning with its pros and cons as detailed above.
What is the best way to learn machine learning?
There are some good online courses and summary pages. It all depends on one’s skills and tastes. My personal advice: Think of machine learning as statistical programming. Beef up on your math and avoid all sources that equate machine learning with neural networks.
What are the advantages and disadvantages of artificial neural networks?
Some advantages: no math, feature engineering, or artisan skills required; easy to train; may uncover aspects of the problem not originally considered. Some disadvantages: requires relatively more data; tedious preparation work; leaves no explanation as to why they decide the way they do, overfitting.
Peter Hussami
Budapest, Hungary
Member since July 3, 2017
About the author
Peter’s rare math-modeling expertise includes audio and sensor analysis, ID verification, NPL, scheduling, routing, and credit scoring.
Expertise
PREVIOUSLY AT