Genetic Algorithms: Search and Optimization by Natural Selection
Many problems have optimal algorithms developed for them, while many others require us to randomly guess until we get a good answer. Even an optimal solution becomes slow and complex at a certain scale, at which point we can turn to natural processes to see how they reach acceptable results.
In this article, Toptal Freelance Software Engineer Eugene Ossipov walks us through the basics of creating a Genetic Algorithm and gives us the knowledge to delve deeper into solving any problems using this approach.
Many problems have optimal algorithms developed for them, while many others require us to randomly guess until we get a good answer. Even an optimal solution becomes slow and complex at a certain scale, at which point we can turn to natural processes to see how they reach acceptable results.
In this article, Toptal Freelance Software Engineer Eugene Ossipov walks us through the basics of creating a Genetic Algorithm and gives us the knowledge to delve deeper into solving any problems using this approach.
Eugene (MCS) has spent over two decades as an architect and developer, including for the Bank of Montreal, TD Bank, and RBC.
Expertise
PREVIOUSLY AT

What Are Genetic Algorithms?
Over the past few years, there has been a terrific buzz around Artificial Intelligence (AI). Major companies like Google, Apple, and Microsoft are actively working on the topic. In fact, AI is an umbrella that covers lots of goals, approaches, tools, and applications. Genetic Algorithms (GA) is just one of the tools for intelligent searching through many possible solutions.
GA is a metaheuristic search and optimization technique based on principles present in natural evolution. It belongs to a larger class of evolutionary algorithms.
GA maintains a population of chromosomes—a set of potential solutions for the problem. The idea is that “evolution” will find an optimal solution for the problem after a number of successive generations—similar to natural selection.
GA mimics three evolutionary processes: selection, gene crossover, and mutation.
Similar to natural selection, the central concept of GA selection is fitness. The chromosomes that are more fit have a better chance for survival. Fitness is a function that measures the quality of the solution represented by the chromosome. In essence, each chromosome within the population represents the input parameters. For example, if your problem contains two input parameters, such as price and volume in trading, each chromosome will logically consist of two elements. How the elements are encoded within the chromosome is a different topic.
During the selection, chromosomes form pairs of parents for breeding. Each child takes characteristics from its parents. Basically, the child represents a recombination of characteristics from its parents: Some of the characteristics are taken from one parent and some from another. In addition to the recombination, some of the characteristics can mutate.
Because fitter chromosomes produce more children, each subsequent generation will have better fitness. At some point, a generation will contain a chromosome that will represent a good enough solution for our problem.
GA is powerful and broadly applicable for complex problems. There is a large class of optimization problems that are quite hard to solve by conventional optimization techniques. Genetic algorithms are efficient algorithms whose solution is approximately optimal. The well-known applications include scheduling, transportation, routing, group technologies, layout design, neural network training, and many others.
Putting Things into Practice
The example we’ll look at can be considered the “Hello World” of GA. This example was initially given by J. Freeman in Simulating Neural Networks with Mathematica. I took it from Genetic Algorithms and Engineering Design by Mitsuo Gen and Runwei Cheng.
The Word-Matching Problem tries to evolve an expression with a genetic algorithm. Initially, the algorithm is supposed to “guess” the “to be or not to be” phrase from randomly-generated lists of letters.
Since there are 26 possible letters for each of 13 locations [excluding whitespace] in the list, the probability that we get the correct phrase in a pure random way is (1/26)^13=4.03038×10-19, which is about two chances out of a [quintillion] (Gen & Chong, 1997).
We’ll define the problem a bit more widely here, making the solution even more difficult. Let’s assume that we are not limited to English language or a specific phrase. We can end up dealing with any alphabet, or even any set of symbols. We have no knowledge of the language. We don’t even know if there is any language at all.
Let’s say our opponent thought of an arbitrary phrase, including whitespace. We know the length of the phrase and the count of symbols in the alphabet. That is the only knowledge we have. After each guess, our opponent tells us how many letters are in place.
Each chromosome is a sequence of indices of the symbols in the alphabet. If we are talking about the English alphabet, then ‘a’ will be represented by 0, ‘b’ by 1, ‘c’ by 2, and so on. So, for example, the word “be” will be represented as [4, 1].
We will demonstrate all steps through Java code snippets, but knowledge of Java is not required to understand each step.
Genetic Algorithm Core
We can start with a general implementation of the genetic algorithm:
public void find() {
// Initialization
List<T> population = Stream.generate(supplier)
.limit(populationSize)
.collect(toList());
// Iteration
while (!termination.test(population)) {
// Selection
population = selection(population);
// Crossover
crossover(population);
// Mutation
mutation(population);
}
}
This is the simple set of steps that every GA more or less consists of. At the initialization step, we generate an initial population of phrases. The size of the population is determined by populationSize. How the phrase is generated depends on implementation of the supplier.
Within the iteration step, we evolve the population until the termination conditions are met within the while loop’s test. The termination conditions may include both the number of generations and the exact match of one of the phrases in the population. The termination encapsulates an exact implementation.
Within each iteration, we perform the typical GA steps:
- Perform a selection over the population based on chromosome fitness.
- Produce a new “generation” via the crossover operation.
- Perform a recombination of some letters in some phrases.
The core of the algorithm is very simple and domain-agnostic. It will be the same for all problems. What you will need to tune is the implementation of genetic operators. Next, we will take a close look at each of the GA operators previously mentioned.
Selection
As we already know, selection is a process of finding successors to the current chromosomes—the chromosomes that are more fit for our problem. During the selection, we need to ensure that the chromosomes with better fitness have a better chance for survival.
private List<T> selection(List<T> population) {
final double[] fitnesses = population.stream()
.mapToDouble(fitness)
.toArray();
final double totalFitness = DoubleStream.of(fitnesses).sum();
double sum = 0;
final double[] probabilities = new double[fitnesses.length];
for (int i = 0; i < fitnesses.length; i++) {
sum += fitnesses[i] / totalFitness;
probabilities[i] = sum;
}
probabilities[probabilities.length - 1] = 1;
return range(0, probabilities.length).mapToObj(i -> {
int index = binarySearch(probabilities, random());
if (index < 0) {
index = -(index + 1);
}
return population.get(index);
}).collect(toList());
}
The idea behind this implementation is the following: The population is represented as consequent ranges on the numerical axis. The whole population is between 0 and 1.
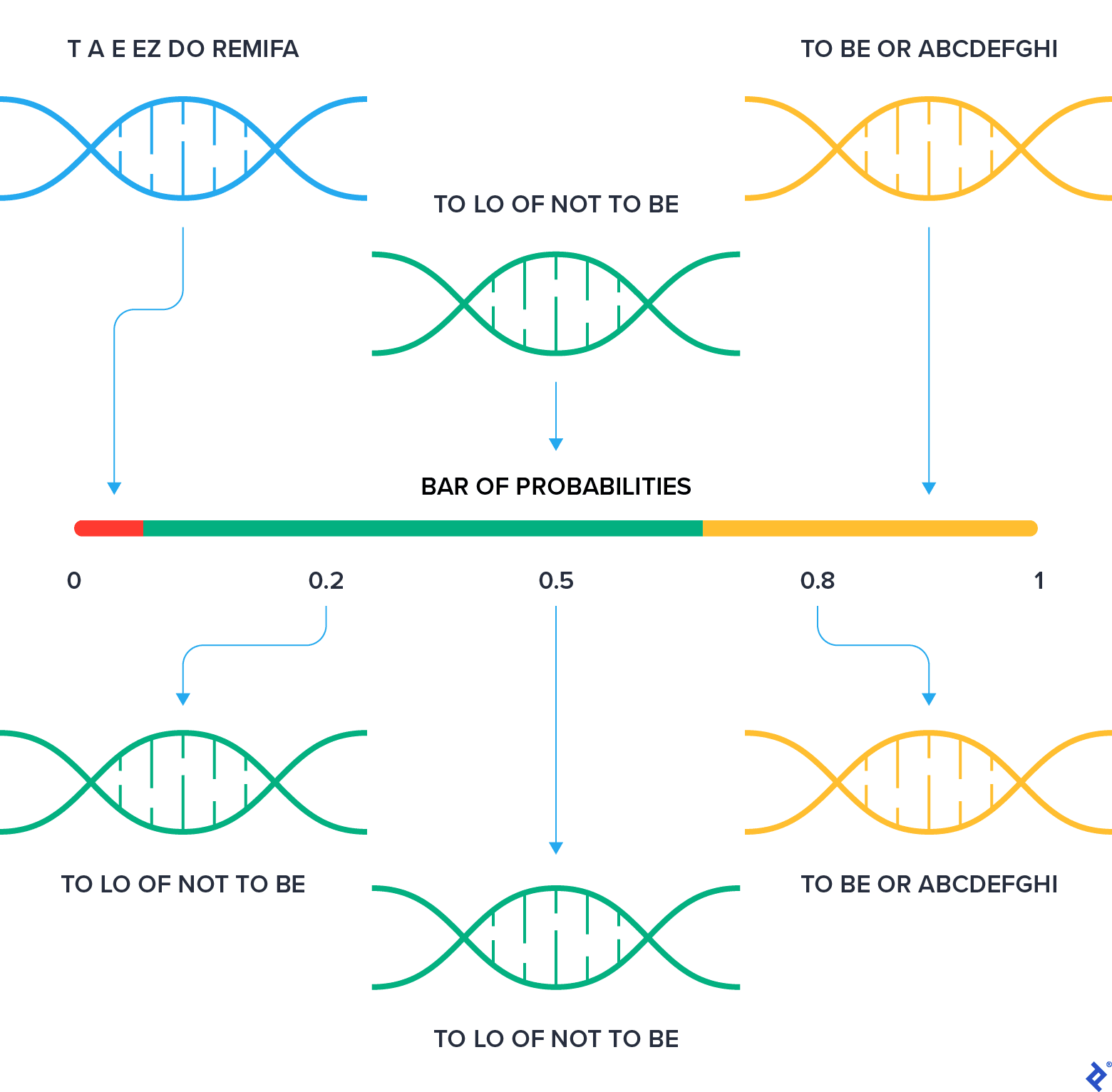
The chunk of the range that a chromosome takes is proportional to its fitness. This results in a fitter chromosome getting a bigger chunk. Then we randomly peek at a number between 0 and 1 and find a range that includes the number. Obviously, bigger ranges have higher chances to be selected, and therefore fitter chromosomes have a better chance for survival.
Because we don’t know details about the fitness function, we need to normalize the fitness values. The fitness function is represented by fitness, which converts a chromosome into an arbitrary double that represents the fitness of the chromosome.
In the code, we find fitness rates for all chromosomes in the population, and we also find the total fitness. Within the for loop, we perform a cumulative sum over probabilities scaled down by total fitness. Mathematically, this should result in the final variable having the value of 1. Due to the imprecision of floating point, we cannot guarantee that, so we set it to 1 just to be sure.
Finally, for a number of times equal to the number of input chromosomes, we generate a random number, find a range that includes the number, and then select the corresponding chromosome. As you may notice, the same chromosome may be selected multiple times.
Crossover
Now we need to the chromosomes to “breed.”
private void crossover(List<T> population) {
final int[] indexes = range(0, population.size())
.filter(i-> random() < crossoverProbability)
.toArray();
shuffle(Arrays.asList(indexes));
for (int i = 0; i < indexes.length / 2; i++) {
final int index1 = indexes[2 * i];
final int index2 = indexes[2 * i + 1];
final T value1 = population.get(index1);
final T value2 = population.get(index2);
population.set(index1, crossover.apply(value1, value2));
population.set(index2, crossover.apply(value2, value1));
}
}
With the predefined probability crossoverProbability, we select parents for breeding. The selected parents are shuffled, allowing any combinations to happen. We take pairs of parents and apply the crossover operator. We apply the operator twice for each pair because we need to keep the size of the population the same. The children replace their parents in the population.
Mutation
Finally, we perform recombination of the characteristics.
private void mutation(List<T> population) {
for (int i = 0; i < population.size(); i++) {
if (random() < mutationProbability) {
population.set(i, mutation.apply(population.get(i)));
}
}
}
With predefined probability mutationProbability, we perform “mutation” on the chromosomes. The mutation itself is defined by mutation.
Problem-specific Algorithm Configuration
Now let’s take a look at what type of problem-specific parameters we need to provide to our generic implementation.
private BiFunction<T, T, T> crossover;
private double crossoverProbability;
private ToDoubleFunction<T> fitness;
private Function<T, T> mutation;
private double mutationProbability;
private int populationSize = 100;
private Supplier<T> supplier;
private Predicate<Collection<T>> termination;
The parameters, respectively, are:
- Crossover operator
- Crossover probability
- Fitness function
- Mutation operator
- Mutation probability
- Size of the population
- Chromosome supplier for the initial population
- Termination function
Here is the configuration for our problem:
new GeneticAlgorithm<char[]>()
.setCrossover(this::crossover)
.setCrossoverProbability(0.25)
.setFitness(this::fitness)
.setMutation(this::mutation)
.setMutationProbability(0.05)
.setPopulationSize(100)
.setSupplier(() -> supplier(expected.length))
.setTermination(this::termination)
.find()
Crossover Operator and Probability
private char[] crossover(char[] value1, char[] value2) {
final int i = (int) round(random() * value1.length);
final char[] result = new char(value1.length);
System.arraycopy(value1, 0, result, 0, i);
System.arraycopy(value2, i, result, i, value2.length - i);
return result;
}
The probability of crossover is 0.25, so we expect that on average 25 percent of the chromosomes will be selected for crossover. We perform a simple procedure for the crossover of a pair of chromosomes. We generate a random number n from the range [0..length], where length is the length of a chromosome. Now we mate the selected pair by taking the first n characters from one chromosome and the remaining characters after from the second one.
Fitness Function
private double fitness(char[] value) {
return range(0, value.length)
.filter(i -> value[i] == expected[i])
.count();
}
The fitness function simply counts the number of matches between the target phrase and the given chromosome.
Mutation Operator and Probability
private char[] mutation(char[] value) {
final char[] result = Arrays.copyOf(value, value.length);
for (int i = 0; i < 2; i++) {
int letter = (int) round(random() * (ALPHABET.length - 1));
int location = (int) round(random() * (value.length - 1));
result[location] = ALPHABET[letter];
}
return result;
}
The mutation operation is performed independently on each chromosome. The probability of mutation is 0.05, so we expect that, on average, five percent of the population will be mutated. We mutate by picking a random letter position and replacing its value with a random letter from the alphabet. We do it twice for each mutated chromosome.
Supplier
private char[] supplier(int length) {
final char[] result = new char(length);
for (int i = 0; i < length; i++) {
int letter = (int) round(random() * (ALPHABET.length - 1));
result[i] = ALPHABET[letter];
}
return result;
}
The supplier generates random phrases by taking random letters from the alphabet. Each phrase has a constant predefined length.
Termination Function
private boolean termination(Collection<char[]> chars) {
count++;
final Optional<char[]> result = chars.stream()
.filter(value -> round(fitness(value)) == expected.length)
.findAny();
if (result.isPresent()) {
System.out.println("Count: " + count);
System.out.println(result.get());
return true;
}
final boolean terminated = count == 3000;
if (terminated) {
chars.forEach(System.out::println);
}
return terminated;
}
The termination function counts the number of calls and returns true if there is either an exact match, or if the generation count reaches 3,000.
Execution
Now we are ready to test our algorithm. If you run it several times, you will notice that not all runs are successful. Each time, the number of iterations will be different. That is due to the probabilistic nature of the algorithm. The algorithm has several points where it can be improved. You can play with crossover and mutation probabilities.
Lowering the number will lead to a stable but slow solution. A smaller number of chromosomes will be affected by genetic operators and, therefore, more iterations will be required for the solution.
Increasing the numbers will speed up the algorithm, but it will also make the solution unstable. Fit chromosomes will be not only preserved, but also will be affected by the genetic operators. Therefore, they will lose their “good” genes.
It is important to find a good balance. Increasing the number of iterations will give the algorithm more opportunities to find a solution but, on other hand, it will take more time. You also can apply different methods of crossover and mutation. A good selection of these operators will drastically improve the quality of the solution.
What Next?
We’ve covered just the tip of the iceberg here. We took an example that has only one input, and the input can be easily presented as a chromosome. The genetic operators are plain and simple.
It is very interesting to take a real-world problem and apply the genetic algorithm to it. You will discover different approaches in encoding real input data as well as different crossover and mutation implementations.
If a problem can be expressed through a set of parameters that we have to guess to optimize a metric, we can quickly set up a GA that we can use to solve it.
One of the most interesting problems is teaching artificial neural networks. We can set the optimizable parameters to be synapse strengths, and the fitness metric to be the percentage of inputs for which our neural network gave the right answer. After that, we can sit back and let our neural network evolve into the ideal solution we desire. Or at least until we get something good enough, because evolution takes time.
Eugene Ossipov
Barrie, ON, Canada
Member since November 21, 2016
About the author
Eugene (MCS) has spent over two decades as an architect and developer, including for the Bank of Montreal, TD Bank, and RBC.
Expertise
PREVIOUSLY AT


