Architecting Optimization Algorithms with HorusLP

Operations research and convex optimization is a field of applied mathematics that has found wide-ranging commercial applications over the years. As computing power became more affordable and widely available, researchers began building increasingly sophisticated optimization algorithms to help them make better decisions. Today, applications powered by operations research power everything from routing in global logistics to electricity production smoothing in the energy industry.

As the underlying technology grew in complexity, a new set of tools has been created to help researchers and developers work more productively. These tools, such as AMPL, CVXPY, and PuLP, allow developers to quickly define, build, and run optimization algorithms and interface with a wide variety of solvers.

However, while optimization technologies and business needs continue to grow in sophistication, most of these tools have stayed more or less the same and did not evolve quickly enough to meet industry needs. As a result, developing, managing, debugging, and tuning these algorithms often requires a large amount of cognitive overhead, especially in a fast-moving business environment.

Today, I’d like to introduce HorusLP, a Python optimization library that helps with the architecture of algorithm development workflows. We will talk about the problems that the tool is designed to solve, then provide a quick overview of the Python library, and we will build some example optimization algorithms.

Problems Facing Optimization Algorithm Developers

One of the perennial problems facing most developers is the balance between building a maintainable, efficient, idiomatic software and delivering a product within the time constraints of the project. Whether you’re working on a browser-based application, a web API, or a user authentication microservice, there is often a tradeoff between the “right” way and the “fast” way of accomplishing your goals. This inherent tradeoff becomes more salient as product complexity increases.

In most disciplines, a developer can alleviate this problem by choosing a framework or library that helps with the architecture. In the web-facing front-end, many developers choose React or Angular; in the world of API development, software engineers may choose from Django, ASP.NET MVC, or Play, among many others. However, when it comes to the humble optimization algorithm developer, there are very few architecture tools to help manage the architectural complexity. The developer is left to manage variables, constraints, and various objectives on their own. What’s more, operations research algorithms are generally difficult to introspect, exacerbating the problem.

The main purpose of HorusLP is to provide an architectural framework for developing optimization algorithms. By providing structural consistency, the framework makes organization easier and allows developers to focus on what they do best: building algorithms.

Typical Optimization Workflow Challenges

There are several major sources of complexity when developing OR algorithms:

Complexity from variables

• Variables often have to be added to accommodate additional business requirements and there is no easy way to track them for use in model definitions and reporting later on.
• Related variables need to be grouped and tracked, and there isn’t an obvious way to manage them.

Complexity from constraints

• Constraints need to be added and removed to support various scenarios and to perform debugging, but there isn’t an obvious place to add or remove constraints.
• Constraints are often related/dependent on each other, and there is no natural way to express their relationships.

Complexity from objectives

• Objective expressions can become unwieldy if they have multiple components. This can be exacerbated if the various components are weighted, and the weights need to be adjusted based on business requirements.

Complexity from debugging

• There is no easy way to see the results of the model during development. A developer has to explicitly print new variables and constraint values to see the results. This leads to duplicated code and slower development.
• When adding a constraint causes the model to become infeasible, it may not be obvious why the constraint caused the model to become infeasible. Usually, developers have to take out various constraints and search for the incompatibility through trial and error

HorusLP hopes to make these challenges more manageable by providing structure, tooling, best practices to improve developer productivity and product maintainability.

HorusLP Tutorial: Optimization Algorithm and Overview of the API

Without further ado, let’s dive in and see what the HorusLP library can do for you!

Since HorusLP is based on Python and PuLP, we’ll want to install them using pip. Run the following in your command line:

Pip install horuslp pulp

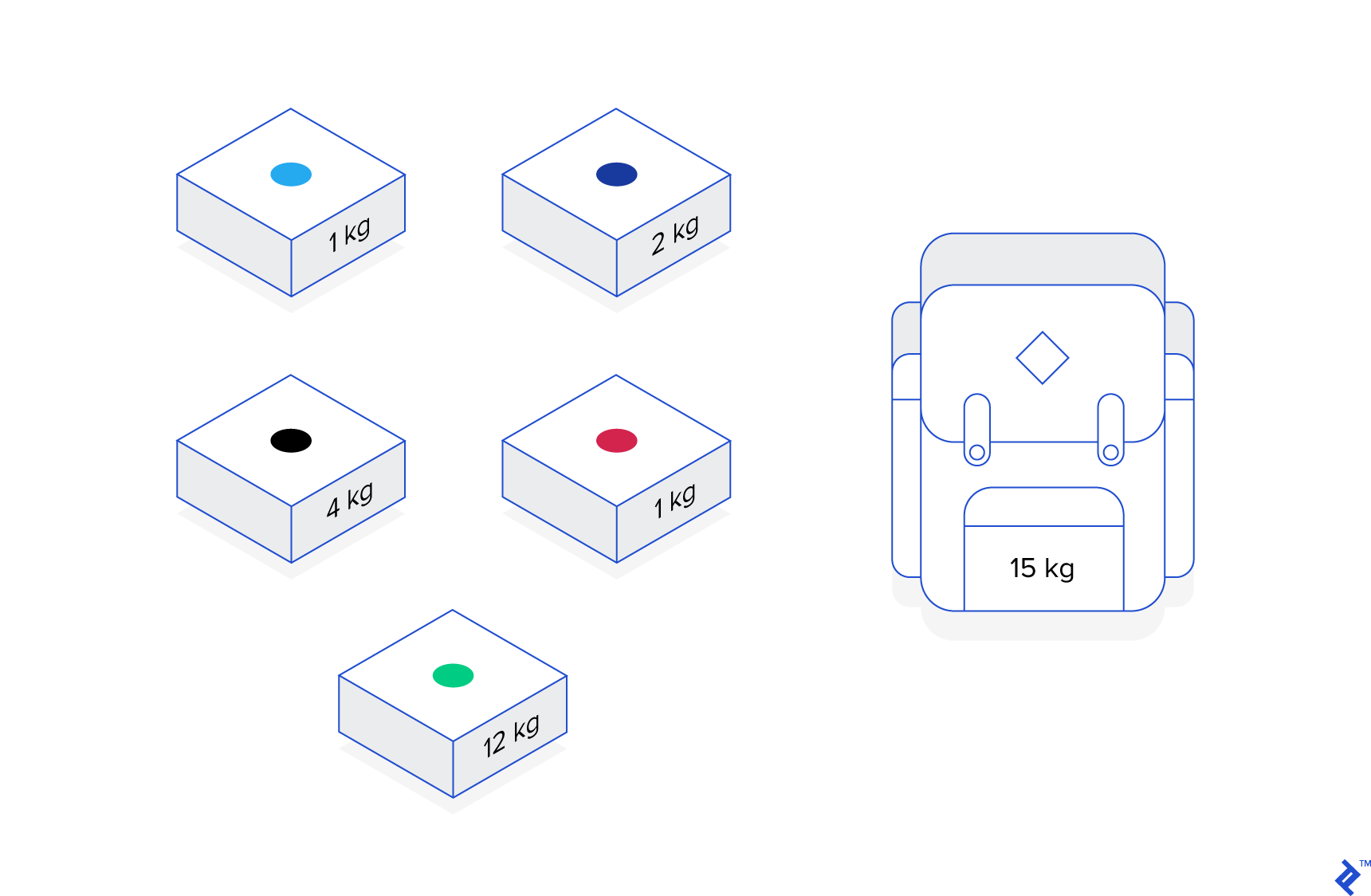
Once the installation is complete, let’s go ahead and open a Python file. We will implement the knapsack problem from my earlier article on operations research.

The HorusLP library has a very simple declarative API and very little boilerplate. Let’s begin by importing the necessary classes and variables:

from horuslp.core.Variables import BinaryVariable # we will be using binary variables, so we will import the BinaryVariable class
from horuslp.core import Constraint, VariableManager, Problem, ObjectiveComponent # We will also need to import the constraint class, variable manager class, the main problem class, and the objective class to define the objective. 
from horuslp.core.constants import MAXIMIZE  # since we're maximizing the resulting value, we want to import this constant

Once we have imported all the variables, let’s define the variables we need for this problem. We do this by creating a variables manager subclass and populating it with the binary variables:

class KnapsackVariables(VariableManager):
    vars = [
        BinaryVariable('camera'), # the first argument is the name of the variable
        BinaryVariable('figurine'),
        BinaryVariable('cider'),
        BinaryVariable('horn')
    ]

Now that the variables are defined, let’s define the constraints. We create constraints by subclassing the main constraint class and implementing its “define” function.

class SizeConstraint(Constraint):
    def define(self, camera, figurine, cider, horn):
        return 2 * camera + 4 * figurine + 7 * cider + 10 * horn <= 15

In the define function, you can ask for the required variables by name. The framework will locate the variable in the variable manager and pass it into the define function.

After the constraint is implemented, we can implement the objective. Since it is a simple objective, we will use ObjectiveComponent:

class ValueObjective(ObjectiveComponent):
    def define(self, camera, figurine, cider, horn):
        return 5 * camera + 7 * figurine + 2 * cider + 10 * horn

The define function has a very similar setup to the constraint class’s define function. Instead of returning a constraint expression, however, we return an affine expression.

Now that the variables, constraints, and objectives are defined, let’s define the model:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = ValueObjective
    constraints = [SizeConstraint]
    sense = MAXIMIZE

To build the model, we create a class that is a subclass of the Problem class and specify the variables, objectives, constraints, and the sense. With the problem specified, we can solve the problem:

prob = KnapsackProblem()
prob.solve()

After the solve, we can print the results using the problem class’s print_results function. We can also access the value of specific variables by looking at the result_variables class.

prob.print_results()
print(prob.result_variables)

Run the script, and you should see the following output:

KnapsackProblem: Optimal
camera 0.0
figurine 1.0
cider 0.0
horn 1.0
ValueObjective: 17.00
SizeConstraint: 14.00
{'camera': 0.0, 'figurine': 1.0, 'cider': 0.0, 'horn': 1.0}

You should see the problem status, the final value of the variables, the objective value, and the value of the constraint expression. We also see the resulting values of the variables as a dictionary.

And there we have it, our first HorusLP problem in about 35 lines!

In the coming examples, we’ll explore some more sophisticated features of the HorusLP library.

Using VariableGroups

Sometimes, variables are related and belong to a logical group. In the case of the knapsack problem, all variables can be placed into an object group. We can refactor the code to use the variable group. Be sure the save the code from the previous section as we will refer to it in subsequent tutorials!

Change the import statements like so:

from horuslp.core.Variables import BinaryVariableGroup
from horuslp.core import Constraint, VariableManager, Problem, ObjectiveComponent
from horuslp.core.constants import MAXIMIZE

Now we also need to change the knapsack variable declarations like so:

class KnapsackVariables(VariableManager):
    vars = [
        BinaryVariableGroup('objects', [
            'camera',
            'figurine',
            'cider',
            'horn'
        ])
    ]

The first argument is the variable group’s name, the second variable is a list of names for the variables within that group.

Now we need to change the constraint and objective definitions. Instead of asking for the individual names, we will as for the variable group, which will be passed in as a dictionary where the keys are the names and the values are the variables. Change the constraint and objective definitions like so:

class SizeConstraint(Constraint):
    def define(self, objects):
        return 2 * objects['camera'] + 4 * objects['figurine'] + 7 * objects['cider'] + 10 * objects['horn'] <= 15

class ValueObjective(ObjectiveComponent):
    def define(self, objects):
        return 5 * objects['camera'] + 7 * objects['figurine'] + 2 * objects['cider'] + 10 * objects['horn']

Now we can use the same problem definition and run commands:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = ValueObjective
    constraints = [SizeConstraint]
    sense = MAXIMIZE


prob = KnapsackProblem()
prob.solve()
prob.print_results()
print(prob.result_variables)

You should see this in your output:

KnapsackProblem: Optimal
objects[camera] 0.0
objects[figurine] 1.0
objects[cider] 0.0
objects[horn] 1.0
ValueObjective: 17.00
SizeConstraint: 14.00
{'objects': {'camera': 0.0, 'figuring': 1.0, 'cider': 0.0, 'horn': 1.0}}

Managing Multiple Constraints

Models with a single constraint are relatively rare. When working with multiple constraints, it is good to have all of the constraints in one place so that they can be tracked and managed easily. HorusLP makes that natural.

Suppose, for example, we wanted to see how the results would change if we forced the model to add a camera to our knapsack. We would implement an additional constraint and add it to our problem definition.

Go back to the model we implemented in the first tutorial. Add the following constraint:

class MustHaveItemConstraint(Constraint):
    def define(self, camera):
        return camera >= 1

To add the constraint to the model, we simply need to add it to the problem definition like so:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = ValueObjective
    constraints = [
        SizeConstraint,
        MustHaveItemConstraint # just add this line :)
    ]
    sense = MAXIMIZE

Run the problem, and you should see the following output:

KnapsackProblem: Optimal
camera 1.0
figurine 0.0
cider 0.0
horn 1.0
ValueObjective: 15.00
SizeConstraint: 12.00
MustHaveItemConstraint: 1.00

You should see the new constraint being printed in the stdout, and the changed optimal variable values.

Managing Dependent Constraints and Constraint Groups

Constraints are often related to each other either because they’re dependent on each other, or because they logically belong to the same group.

For example, if you want to set a constraint to limit the sum of absolute value of a set of variables, you must first specify constraints to express the absolute value relationships between the intended variables, and then specify the absolute value limits. Sometimes, you need to apply similar constraints to a group of variables to express a specific relationship between variables.

To express these groupings, we can use the dependent constraints feature of our constraint definitions. To see how the dependent constraint feature can be used, refactor the SizeConstraint of the previous problem like so:

class SizeConstraint(Constraint):
    dependent_constraints = [MustHaveItemConstraint]

    def define(self, camera, figurine, cider, horn):
        return 2 * camera + 4 * figurine + 7 * cider + 10 * horn <= 15

And now to test that dependent constraints are automatically implemented, let’s take the MustHaveItemConstraint out of the problem definition:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = ValueObjective
    constraints = [
        SizeConstraint,
    ]
    sense = MAXIMIZE

And run the code again, and you should see the following in stdout:

KnapsackProblem: Optimal
camera 1.0
figurine 0.0
cider 0.0
horn 1.0
ValueObjective: 15.00
SizeConstraint: 12.00
MustHaveItemConstraint: 1.00

Looks like the MustHaveItemConstraint is implemented! For a more complex example of how dependent constraint can be used, refer to the staffing example at the end of the tutorial.

Managing Multiple Weighted Objectives

Often, during the development of our optimization algorithms, we will encounter an objective expression comprised of multiple parts. As part of our experimentation, we may change the weighing of various objective components to bias the algorithm toward the desired outcome. The CombinedObjective provides a clean and simple way to express this.

Suppose we wanted to bias the algorithm to choose the figurine and the cider. Let’s refactor the code from the previous section to use CombinedObjective.

First, import the CombinedObjective class like so:

from horuslp.core import CombinedObjective

We can implement an independent objective component like so:

class ILoveCiderFigurineObjectiveComponent(ObjectiveComponent):
    def define(self, figurine, cider):
        return figurine + cider

Now we can combine the value objective and the cider/figurine objective by implementing a CombinedObjective:

class Combined(CombinedObjective):
    objectives = [
        (ILoveCiderFigurineObjectiveComponent, 2), # first argument is the objective, second argument is the weight
        (ValueObjectiveComponent, 1)
    ]

Now let’s change the problem definition like so:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = Combined
    constraints = [SizeConstraint]
    sense = MAXIMIZE

Run the problem, and you should see the following output:

KnapsackProblem: Optimal
camera 1.0
figurine 1.0
cider 1.0
horn 0.0
Combined: 18.00
ILoveCiderFigurineObjectiveComponent: 2.00 * 2
ValueObjectiveComponent: 14.00 * 1
SizeConstraint: 13.00
MustHaveItemConstraint: 1.00

The output will outline the combined objective value, the value of each of the objective components, the weight, and of course of the value of all the constraints.

Finding Incompatible Constraints

When developing algorithms, we often run into infeasible models. If the model is complex, it can be challenging to determine why the model is suddenly infeasible. HorusLP has a handy tool to help you in those cases.

Suppose we were adding constraints and ended up with the following set of constraints:

class SizeConstraint(Constraint):
    def define(self, camera, figurine, cider, horn):
        return 2 * camera + 4 * figurine + 7 * cider + 10 * horn <= 15


class SizeConstraint2(Constraint):
    def define(self, camera, figurine, cider, horn):
        return 2 * camera + 4 * figurine + 7 * cider + 10 * horn <= 20


class MustHaveItemConstraint(Constraint):
    def define(self, cider):
        return cider >= 1

class IncompatibleConstraint1(Constraint):
    def define(self, camera):
        return camera >= 1


class IncompatibleConstraint2(Constraint):
    def define(self, camera):
        return camera <= 0

We have a couple of constraints on the total size of the items in the knapsack, a constraint requiring that cider must be in the knapsack, and an incompatible set of constraints that require the camera to be both in and not in the knapsack. (Of course, in a real-world algorithm, the constraints are usually not as obvious and involve complex variable relationships and constraints.)

Suppose also that the constraints are grouped in the following manner, perhaps making detection more difficult:

class CombinedConstraints1(Constraint):
    dependent_constraints = [SizeConstraint2, IncompatibleConstraint1]


class CombinedConstraints2(Constraint):
    dependent_constraints = [SizeConstraint, IncompatibleConstraint2]

# MustHaveItemConstraint will be included in the problem definition independently

Here is the problem definition:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    objective = ValueObjective
    constraints = [CombinedConstraints1, CombinedConstraints2, MustHaveItemConstraint]
    sense = MAXIMIZE

Run the problem, and you should see the following result:

KnapsackProblem: Infeasible

Oh no! What do we do? If we are using most tools, we must embark on a difficult debugging session where we narrow down the potentially conflicting constraints one by one. Fortunately, HorusLP has an incompatibility search feature to help you narrow down the incompatible constraints faster. The simplest way to use the incompatibility search feature is to change the print_results call thusly:

prob.print_results(find_infeasible=True)

Simple as that! Run the code, and now you should see the following as the output:

KnapsackProblem: Infeasible
Finding incompatible constraints...
Incompatible Constraints: ('CombinedConstraints1', 'CombinedConstraints2')

Great! Now we have established that MustHaveItemConstraint is not the cause of the infeasibility and that the issue is due to CombinedConstraints1 and CombinedConstraints2.

That gives us some information, but between the combined constraints there are four dependent constraints. Can we identify which of the four constraints are incompatible? Well, yes. Modify your print_results call thusly:

prob.print_results(find_infeasible=True, deep_infeasibility_search=True)

This will have the infeasibility search expand the dependent constraints so that we get a much more granular picture of what’s causing the infeasibility. Run this and you should see the following output:

KnapsackProblem: Infeasible
Finding incompatible constraints...
Incompatible Constraints: ('IncompatibleConstraint1', 'IncompatibleConstraint2')

While it is tempting to run deep infeasibility search every time, for realistic problems with a large number of total constraints, deep infeasibility search can become very resource intensive and time-consuming. Therefore, it is best to run the basic infeasibility search to narrow the possibility down and run the deep infeasibility search on a smaller subset after doing some manual investigation.

Building Algorithms from Data Files

When building models, we rarely have the luxury to hard-code every constraint and variable. Oftentimes, our program must be flexible enough to change the model depending on the input data. Suppose that instead of hard-coded input we wanted to build our knapsack problem from the following JSON:

{
  "items": [
    {"name": "camera", "value": 5, "weight": 2},
    {"name": "figurine", "value": 7, "weight": 4},
    {"name": "apple", "value": 2, "weight": 7},
    {"name": "horn", "value": 10, "weight": 10},
    {"name": "banana", "value": 9, "weight": 2}
  ],
  "capacity": 15
}

We can do this by relying on the kwargs’ support of the “define” function that we implement for constraints and objectives.

Let’s modify the code from the simple knapsack problem (the problem we implemented in section 1 of the tutorial). First, let’s put the JSON string into the file. Of course, we would normally read it from an external source, but for the sake of simplicity let’s keep everything in one file. Add the following to your code:

JSON = '''
{
  "items": [
    {"name": "camera", "value": 5, "weight": 2},
    {"name": "figurine", "value": 7, "weight": 4},
    {"name": "apple", "value": 2, "weight": 7},
    {"name": "horn", "value": 10, "weight": 10},
    {"name": "banana", "value": 9, "weight": 2}
  ],
  "capacity": 15
}
'''

Let’s also make sure that our program would be able to parse it. Add the following to your import statements:

Import json

Now, let’s modify our variable setup code thusly:

mip_cfg = json.loads(JSON)

class KnapsackVariables(VariableManager):
    vars = [
        BinaryVariable(i['name']) for i in mip_cfg['items']
    ]

This will define a variable for each of the items in the JSON, and name it appropriately.

Let’s change the constraint and objective definitions like so:

class CapacityConstraint(Constraint):
    def define(self, **kwargs):
        item_dict = {i['name']: i['weight'] for i in mip_cfg['items']}
        return sum(kwargs[name] * item_dict[name] for name in kwargs) <= mip_cfg['capacity']


class ValueObjective(ObjectiveComponent):
    def define(self, **kwargs):
        item_dict = {i['name']: i['value'] for i in mip_cfg['items']}
        return sum(kwargs[name] * item_dict[name] for name in kwargs)

By asking for **kwargs instead of specific variables, the define function gets a dictionary containing all the variables by name. The constraint definition function can then access the variables from the dictionary.

Note: For variable groups, it will be a nested dictionary where the first level is the group name and the second level is the variable name.

The rest is pretty straightforward:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    constraints = [CapacityConstraint]
    objective = ValueObjective
    sense = MAXIMIZE


prob = KnapsackProblem()
prob.solve()
prob.print_results()

Run this program and you should see the following output:

KnapsackProblem: Optimal
camera 1.0
figurine 0.0
apple 0.0
horn 1.0
banana 1.0
ValueObjective: 24.00
CapacityConstraint: 14.00

Defining Custom Metrics in HorusLP

Sometimes, for both debugging and reporting purposes, we will build custom metrics that are not expressed directly in the objective or as a constraint. HorusLP has a feature to make specifying custom metrics simple.

Suppose we wanted to keep track of how many fruits the model from our previous section was putting into the knapsack. To keep track of this we can define a custom metric. Let’s begin by importing the Metrics base class:

From horuslp.core import Metric

Now let’s define the custom metric:

class NumFruits(Metric):
    name = "Number of Fruits"

    def define(self, apple, banana):
        return apple + banana

As you can see, the defined interface looks very similar to those of the constraint and objective component class. If you’ve followed the tutorial thus far, this should be fairly familiar to you.

Now we need to add the metric to the problem definition. The interface here again is very similar to the constraint definition:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    constraints = [CapacityConstraint]
    objective = ValueObjective
    metrics = [NumFruits]
    sense = MAXIMIZE

Run this and you should see the following output:

KnapsackProblem: Optimal
camera 1.0
figurine 0.0
apple 0.0
horn 1.0
banana 1.0
ValueObjective: 24.00
CapacityConstraint: 14.00
Number of Fruits: 1.00

You can see the number of fruits printed at the bottom.

Working Through a More Complex Problem: Two Knapsacks

Let’s work through a slightly more complex example. Suppose that instead of a single knapsack, we have a bag and a suitcase. We also have two classes of objects, durable and fragile. The suitcase, being more protective, can hold both fragile and durable goods. The bag, on the other hand, can only hold durable goods. Suppose also that the data for the items is given in the following JSON:

{
  "fragile": [
    {"name": "camera", "value": 5, "weight": 2},
    {"name": "glasses", "value": 3, "weight": 4},
    {"name": "apple", "value": 2, "weight": 7},
    {"name": "pear", "value": 5, "weight": 3},
    {"name": "banana", "value": 9, "weight": 2}
  ],
  "durable": [
    {"name": "figurine", "value": 7, "weight": 4},
    {"name": "horn", "value": 10, "weight": 10},
    {"name": "leatherman", "value": 10, "weight": 3}
  ],
  "suitcase_capacity": 15,
  "bag_capacity": 20
}

Let’s see how this changes the model. Let’s start with a blank slate as the model will be quite different. Begin with the setup of the problem:

import json
from horuslp.core.Variables import BinaryVariableGroup
from horuslp.core import Constraint, VariableManager, Problem, Metric, ObjectiveComponent
from horuslp.core.constants import MAXIMIZE

JSON = '''
{
  "fragile": [
    {"name": "camera", "value": 5, "weight": 2},
    {"name": "glasses", "value": 3, "weight": 4},
    {"name": "apple", "value": 2, "weight": 7},
    {"name": "pear", "value": 5, "weight": 3},
    {"name": "banana", "value": 9, "weight": 2}
  ],
  "durable": [
    {"name": "figurine", "value": 7, "weight": 4},
    {"name": "horn", "value": 10, "weight": 10},
    {"name": "leatherman", "value": 10, "weight": 3}
  ],
  "suitcase_capacity": 15,
  "bag_capacity": 20
}
'''
mip_cfg = json.loads(JSON)

Now let’s set up the variables. We’ll set up a binary variable for every possible item/container combination.

class KnapsackVariables(VariableManager):
    vars = [
        # suitcase can hold both fragile and durable goods 
        BinaryVariableGroup('suitcase_f', [i['name'] for i in mip_cfg['fragile']]),
        BinaryVariableGroup('suitcase_d', [i['name'] for i in mip_cfg['durable']]),
        # bag can only hold durable goods.
        BinaryVariableGroup('bag_d', [i['name'] for i in mip_cfg['durable']])
    ]

Now we want to implement weight constraints for both the suitcase and the bag.

class SuitcaseCapacityConstraint(Constraint):
    def define(self, suitcase_d, suitcase_f):
        fragile_weight = sum([suitcase_f[i['name']] * i['weight'] for i in mip_cfg['fragile']])
        durable_weight = sum([suitcase_d[i['name']] * i['weight'] for i in mip_cfg['durable']])
        return fragile_weight + durable_weight <= mip_cfg['suitcase_capacity']


class BagCapacityConstraint(Constraint):
    def define(self, bag_d):
        durable_weight = sum([bag_d[i['name']] * i['weight'] for i in mip_cfg['durable']])
        return durable_weight <= mip_cfg['bag_capacity']

Now we need to implement a slightly more complex constraint—the constraint that ensures an item doesn’t go into both the suitcase and the bag—that is, if the “in the suitcase” variable is 1, then the “in the bag” variable needs to be zero, and vice versa. Of course, we want to make sure to allow instances where the item ends up in neither container as well.

To add this constraint, we need to iterate over all the durable items, find the “in the suitcase” variable and the “in the bag” variable and assert that the sum of these variables is less than 1.

We can dynamically define dependent constraints quite easily in HorusLP:

class UniquenessConstraints(Constraint):
    def __init__(self):
        super(UniquenessConstraints, self).__init__()
        # call the dependent constraint builder function for every durable item, and push them into dependent constraints. 
        dependent_constraints = [self.define_uniqueness_constraint(item) for item in mip_cfg['durable']]
        self.dependent_constraints = dependent_constraints

    def define_uniqueness_constraint(self, item):
        # classes are first-class objects in python, so we can define a class within this function and return it
        class UQConstraint(Constraint):
            # we name the constraint based on the item this is for, so that debugging is easier.
            name = "Uniqueness_%s" % item['name']

            def define(self, suitcase_d, bag_d):
                # the define function can access the variables much in the same way as other functions
                return suitcase_d[item['name']] + bag_d[item['name']] <= 1

        return UQConstraint

Now that the constraints are defined, let’s build the objective. The objective is simple the sum of all the values we get from all the items that are in containers. Thus:

class TotalValueObjective(ObjectiveComponent):
    def define(self, suitcase_f, suitcase_d, bag_d):
        fragile_value = sum([suitcase_f[i['name']] * i['weight'] for i in mip_cfg['fragile']])
        durable_value_s = sum([suitcase_d[i['name']] * i['weight'] for i in mip_cfg['durable']])
        durable_value_d = sum([bag_d[i['name']] * i['weight'] for i in mip_cfg['durable']])
        return fragile_value + durable_value_s + durable_value_d

Let’s also define some custom metrics so we can see at a glance how much weight was put into the bag and the suitcase, as well as how much of the suitcase weight came from durable goods and fragile goods:

class SuitcaseFragileWeightMetric(Metric):
    def define(self, suitcase_f):
        return sum([suitcase_f[i['name']] * i['weight'] for i in mip_cfg['fragile']])


class SuitcaseDurableWeightMetric(Metric):
    def define(self, suitcase_d):
        return sum([suitcase_d[i['name']] * i['weight'] for i in mip_cfg['durable']])


class BagWeightMetric(Metric):
    def define(self, bag_d):
        return sum([bag_d[i['name']] * i['weight'] for i in mip_cfg['durable']])

Now we have all the pieces finished, let’s instantiate the problem and run the model:

class KnapsackProblem(Problem):
    variables = KnapsackVariables
    constraints = [SuitcaseCapacityConstraint, BagCapacityConstraint, UniquenessConstraints]
    objective = TotalValueObjective
    metrics = [SuitcaseDurableValueMetric, SuitcaseFragileValueMetric, BagValueMetric]
    sense = MAXIMIZE

prob = KnapsackProblem()
prob.solve()
prob.print_results()

Run this, and you should see the following output in your stdout:

KnapsackProblem: Optimal
suitcase_f[camera] 1.0
suitcase_f[glasses] 1.0
suitcase_f[apple] 1.0
suitcase_f[pear] 0.0
suitcase_f[banana] 1.0
suitcase_d[figurine] 0.0
suitcase_d[horn] 0.0
suitcase_d[leatherman] 0.0
bag_d[figurine] 1.0
bag_d[horn] 1.0
bag_d[leatherman] 1.0
TotalValueObjective: 32.00
SuitcaseCapacityConstraint: 15.00
BagCapacityConstraint: 17.00
Uniqueness_figurine: 1.00
Uniqueness_horn: 1.00
Uniqueness_leatherman: 1.00
SuitcaseDurableWeightMetric: 0.00
SuitcaseFragileWeightMetric: 15.00
BagWeightMetric: 17.00

So the camera, glasses, apple, and banana go into the suitcase for a total of 15 weight units, the figurine, horn, and leatherman all go into the bag for a total of 17 weight. The total value of the goods comes out to 32 value units. Interestingly, none of the durable goods ended up in the suitcase, most likely because the bag had enough capacity to hold all the durable goods.

A Larger and More Realistic Scenario: The Staffing Problem

If you’ve made it this far in our HorusLP tutorial, congratulations! You now have a good idea of how to use HorusLP.

However, all of the examples we’ve been working on have thus far been permutations of the knapsack problem, and some of the requirements and parameters are a bit unrealistic. Let’s work through one more problem together to see how HorusLP can solve a more realistic problem. We’ll work through the staffing problem outlined in the second half of my previous Toptal article.

In the interest of time, we will go straight for the final version of the model (with personal conflicts, labor regulations, and temp worker allowances) but the implementation of the initial simpler model is available on GitHub as well.

So let’s begin by setting up the problem:

from horuslp.core.Variables import BinaryVariableGroup, IntegerVariableGroup
from horuslp.core import Constraint, VariableManager, Problem, ObjectiveComponent, CombinedObjective
from horuslp.core.constants import MINIMIZE

shift_requirements = [1, 4, 3, 5, 2]  # the number of workers we need to staff for each shift
# the availability and pay rates of each of the employees
workers = {
    "Melisandre": {
        "availability": [0, 1, 4],
        "cost": 20
    },
    "Bran": {
        "availability": [1, 2, 3, 4],
        "cost": 15
    },
    "Cersei": {
        "availability": [2, 3],
        "cost": 35
    },
    "Daenerys": {
        "availability": [3, 4],
        "cost": 35
    },
    "Theon": {
        "availability": [1, 3, 4],
        "cost": 10
    },
    "Jon": {
        "availability": [0, 2, 4],
        "cost": 25
    },
    "Tyrion": {
        "availability": [1, 3, 4],
        "cost": 30
    },
    "Jaime": {
        "availability": [1, 2, 4],
        "cost": 20
    },
    "Arya": {
        "availability": [0, 1, 3],
        "cost": 20
    }
}

# the following people can't work together, sadly.
ban_list = {
    ("Daenerys", "Jaime"),
    ("Daenerys", "Cersei"),
    ("Jon", "Jaime"),
    ("Jon", "Cersei"),
    ("Arya", "Jaime"),
    ("Arya", "Cersei"),
    ("Arya", "Melisandre"),
    ("Jaime", "Cersei")
}

# Dothraki Staffing Corp will provide us with expensive temp workers
DOTHRAKI_MAX = 10
DOTHRAKI_COST = 45

Now let’s define the variables, which in this case would be binary variables determining if a worker should work their shift, and integer variables determining how many dothrakis we hire for each shift:

class StaffingVariables(VariableManager):
    vars = []

    def __init__(self):
        # like dependent constraints, we can dynamically define variables in the init function
        super(StaffingVariables, self).__init__()
        # regular workers
        varkeys = []
        for employee, availability_info in workers.items():
            for shift in availability_info['availability']:
                varkeys.append((employee, shift))
        self.vars.append(BinaryVariableGroup('employee_shifts', varkeys))
        # dothrakis
        dothraki_keys = [i for i in range(len(shift_requirements))]
        self.vars.append(IntegerVariableGroup('dothraki_workers', dothraki_keys, 0, DOTHRAKI_COST))

Now let’s implement the constraint that requires us to staff sufficiently for every shift:

class SufficientStaffingConstraint(Constraint):
    # we need to staff people sufficiently
    dependent_constraints = []

    def __init__(self):
        super(SufficientStaffingConstraint, self).__init__()
        for shift_num, shift_req in enumerate(shift_requirements):
            self.dependent_constraints.append(self.build_shift_constraint(shift_num, shift_req))

    def build_shift_constraint(self, sn, sr):
        class ShiftConstraint(Constraint):
            name = "shift_requirement_%d" % sn

            def define(self, employee_shifts, dothraki_workers):
                variables = [val for key, val in employee_shifts.items() if key[1] == sn]
                variables.append(dothraki_workers[sn])
                return sum(variables) >= sr
        return ShiftConstraint

Now, we need to implement the constraints preventing specific people from working with each other:

class PersonalConflictsConstraint(Constraint):
    # some people can't work together
    dependent_constraints = []

    def __init__(self):
        super(PersonalConflictsConstraint, self).__init__()
        for person_1, person_2 in ban_list:
            for shift in range(len(shift_requirements)):
                self.dependent_constraints.append(self.build_conflict_constraint(person_1, person_2, shift))

    def build_conflict_constraint(self, p1, p2, s):
        class ConflictConstraint(Constraint):
            name = "Conflict_%s_%s_%d" % (p1, p2, s)

            def define(self, employee_shifts):
                if (p1, s) in employee_shifts and (p2, s) in employee_shifts:
                    return employee_shifts[p1, s] + employee_shifts[p2, s] <= 1
                return True # returning true will make the constraint do nothing
        return ConflictConstraint

And finally the labor standards constraint. We’ll implement this one slightly differently for demonstrative purposes:

class LaborStandardsConstraint(Constraint):
    # we can make someone work more than two shifts a day.
    dependent_constraints = []

    def __init__(self):
        super(LaborStandardsConstraint, self).__init__()
        for worker in workers.keys():
            # we don't need a constraint builder function, but in those circumstances
            # we need to set the needed values as class variables and refer to them
            # via the self keyword due to how python's closure system works
            class LaborConstraint(Constraint):
                # we can't use worker directly!
                wk = worker
                name = "labor_standard_%s" % worker

                def define(self, employee_shifts):
                    # we need to access the worker using self. Change self.wk to worker to see
                    # why we need to do this
                    worker_vars = [var for key, var in employee_shifts.items() if key[0] == self.wk]
                    return sum(worker_vars) <= 2
            self.dependent_constraints.append(LaborConstraint)

And now let’s set up the objectives. The dothraki cost and regular employee costs are calculated very differently, so we’ll put them in separate objective components:

class CostObjective(ObjectiveComponent):
    # this is the cost function for all the named workers
    def define(self, employee_shifts, dothraki_workers):
        costs = [
            workers[key[0]]['cost'] * var for key, var in employee_shifts.items()
        ]
        return sum(costs)


class DothrakiCostObjective(ObjectiveComponent):
    # don't forget the Dothrakis
    def define(self, dothraki_workers):
        dothraki_costs = [
            dothraki_workers[sn] * DOTHRAKI_COST for sn in dothraki_workers
        ]
        return sum(dothraki_costs)


class TotalCostObjective(CombinedObjective):
    objectives = [
        (CostObjective, 1),
        (DothrakiCostObjective, 1)
    ]

And now we can define and run the problem:

class StaffingProblem(Problem):
    variables = StaffingVariables
    objective = TotalCostObjective
    constraints = [SufficientStaffingConstraint, PersonalConflictsConstraint, LaborStandardsConstraint]
    sense = MINIMIZE # we're minimizing this time, not maximizing.


if __name__ == '__main__':
    prob = StaffingProblem()
    prob.solve()
    prob.print_results()

Run the script and you should see the following:

StaffingProblem: Optimal
employee_shifts[('Melisandre', 0)] 0.0
employee_shifts[('Melisandre', 1)] 1.0
employee_shifts[('Melisandre', 4)] 1.0
employee_shifts[('Bran', 1)] 0.0
employee_shifts[('Bran', 2)] 1.0
employee_shifts[('Bran', 3)] 1.0
employee_shifts[('Bran', 4)] 0.0
employee_shifts[('Cersei', 2)] 0.0
employee_shifts[('Cersei', 3)] 0.0
employee_shifts[('Daenerys', 3)] 1.0
employee_shifts[('Daenerys', 4)] 0.0
employee_shifts[('Theon', 1)] 1.0
employee_shifts[('Theon', 3)] 1.0
employee_shifts[('Theon', 4)] 0.0
employee_shifts[('Jon', 0)] 0.0
employee_shifts[('Jon', 2)] 1.0
employee_shifts[('Jon', 4)] 0.0
employee_shifts[('Tyrion', 1)] 1.0
employee_shifts[('Tyrion', 3)] 1.0
employee_shifts[('Tyrion', 4)] 0.0
employee_shifts[('Jaime', 1)] 1.0
employee_shifts[('Jaime', 2)] 0.0
employee_shifts[('Jaime', 4)] 1.0
employee_shifts[('Arya', 0)] 1.0
employee_shifts[('Arya', 1)] 0.0
employee_shifts[('Arya', 3)] 1.0
dothraki_workers[0] 0.0
dothraki_workers[1] 0.0
dothraki_workers[2] 1.0
dothraki_workers[3] 0.0
dothraki_workers[4] 0.0
TotalCostObjective: 335.00
CostObjective: 290.00 * 1
DothrakiCostObjective: 45.00 * 1
shift_requirement_0: 1.00
shift_requirement_1: 4.00
shift_requirement_2: 3.00
shift_requirement_3: 5.00
shift_requirement_4: 2.00
Conflict_Jon_Cersei_2: 1.00
Conflict_Jon_Jaime_2: 1.00
Conflict_Jon_Jaime_4: 1.00
Conflict_Daenerys_Cersei_3: 1.00
Conflict_Daenerys_Jaime_4: 1.00
Conflict_Arya_Jaime_1: 1.00
Conflict_Arya_Cersei_3: 1.00
Conflict_Arya_Melisandre_0: 1.00
Conflict_Arya_Melisandre_1: 1.00
Conflict_Jaime_Cersei_2: 0.00
labor_standard_Melisandre: 2.00
labor_standard_Bran: 2.00
labor_standard_Cersei: 0.00
labor_standard_Daenerys: 1.00
labor_standard_Theon: 2.00
labor_standard_Jon: 1.00
labor_standard_Tyrion: 2.00
labor_standard_Jaime: 2.00
labor_standard_Arya: 2.00

If you compare this with the problem we implemented in the previous tutorial, you should see that the results match.

Wrapping Up

Congratulations for making it through our first HorusLP tutorial! You’re now a competent practitioner of HorusLP.

I hope that this article convinced you of the benefits of architecting your MIP models, and that you will make use of HorusLP in your coming projects. You can find the HorusLP source code, as well as the code for all the tutorials, on GitHub. Additional HorusLP documentation and a tutorial page will be added to GitHub very soon.

As HorusLP is a fairly new project, we would love to hear from you and incorporate your input. If you have any questions, comments, or suggestions, please drop me a line either through Toptal or using the contact information you can find on GitHub. I hope to hear from you soon!