Needle in a Haystack: A Nifty Large-scale Text Search Algorithm Tutorial
When coming across the term “text search,” one usually thinks of a large body of text which is indexed in a way that makes it possible to quickly look up one or more search terms when they are entered by a user. This is a classic problem in computer science to which many solutions exist.
But how about a reverse scenario? What if what’s available for indexing beforehand is a group of search phrases, and only at runtime is a large body of text presented for searching?
When coming across the term “text search,” one usually thinks of a large body of text which is indexed in a way that makes it possible to quickly look up one or more search terms when they are entered by a user. This is a classic problem in computer science to which many solutions exist.
But how about a reverse scenario? What if what’s available for indexing beforehand is a group of search phrases, and only at runtime is a large body of text presented for searching?
Ahmed is an Android expert with a passion for intuitive user experience and snappy app performance.
When coming across the term “text search,” one usually thinks of a large body of text which is indexed in a way that makes it possible to quickly look up one or more search terms when they are entered by a user. This is a classic problem for computer scientists, to which many solutions exist.
But how about a reverse scenario? What if what’s available for indexing beforehand is a group of search phrases, and only at runtime is a large body of text presented for searching? These questions are what this trie data structure tutorial seeks to address.

Applications
A real world application for this scenario is matching a number of medical theses against a list of medical conditions and finding out which theses discuss which conditions. Another example is traversing a large collection of judicial precedents and extracting the laws they reference.
Direct Approach
The most basic approach is to loop through the search phrases, and search through the text each phrase, one by one. This approach does not scale well. Searching for a string inside another has the complexity O(n). Repeating that for m search phrases leads to the awful O(m * n).
The (likely only) upside of a direct approach that it is simple to implement, as apparent in the following C# snippet:
String[] search_phrases = File.ReadAllLines ("terms.txt");
String text_body = File.ReadAllText("body.txt");
int count = 0;
foreach (String phrase in search_phrases)
if (text_body.IndexOf (phrase) >= 0)
++count;
Running this code on my development machine [1] against a test sample [2], I got a runtime of 1 hour 14 minutes – far beyond the time you need to grab a cup of coffee, get up and stretch, or any other excuse developers use to skip work.
A Better Approach - The Trie
The previous scenario can be enhanced in a couple of ways. For example, the search process can be partitioned and parallelized on multiple processors/cores. But the reduction in runtime achieved by this approach (total runtime of 20 minutes assuming perfect division over 4 processors/cores) does not justify the added complexity to coding/debugging.
The best possible solution would be one that traverses the text body only once. This requires search phrases to be indexed in a structure that can be transversed linearly, in parallel with the text body, in one pass, achieving a final complexity of O(n).
A data structure that is especially well-suited for just this scenario is the trie. This versatile data structure is usually overlooked and not as famous as other tree-related structures when it comes to search problems.
Toptal’s previous tutorial on tries provides an excellent introduction to how they are structured and used. In short, a trie is a special tree, capable of storing a sequence of values in such a way that tracing the path from the root to any node yields a valid subset of that sequence.
So, if we can combine all the search phrases into one trie, where each node contains a word, we will have the phrases laid out in a structure where simply tracing from the root downwards, via any path, yields a valid search phrase.
The advantage of a trie is that it significantly cuts search time. To make it easier to grasp for the purposes of this trie tutorial, let’s imagine a binary tree. Traversing a binary tree has the complexity of O(log2n), since each node branches into two, cutting the remaining traversal in half. As such, a ternary tree has the traversal complexity of O(log3n). In a trie, however, the number of child nodes is dictated by the sequence it is representing, and in the case of readable/meaningful text, the number of children is usually high.
Text Search Algorithm
As a simple example, let’s assume the following search phrases:
- “same family”
- “different family”
- “separate existence”
- “members of the league”
Remember that we know our search phrases beforehand. So, we start by building an index, in the form of a trie:
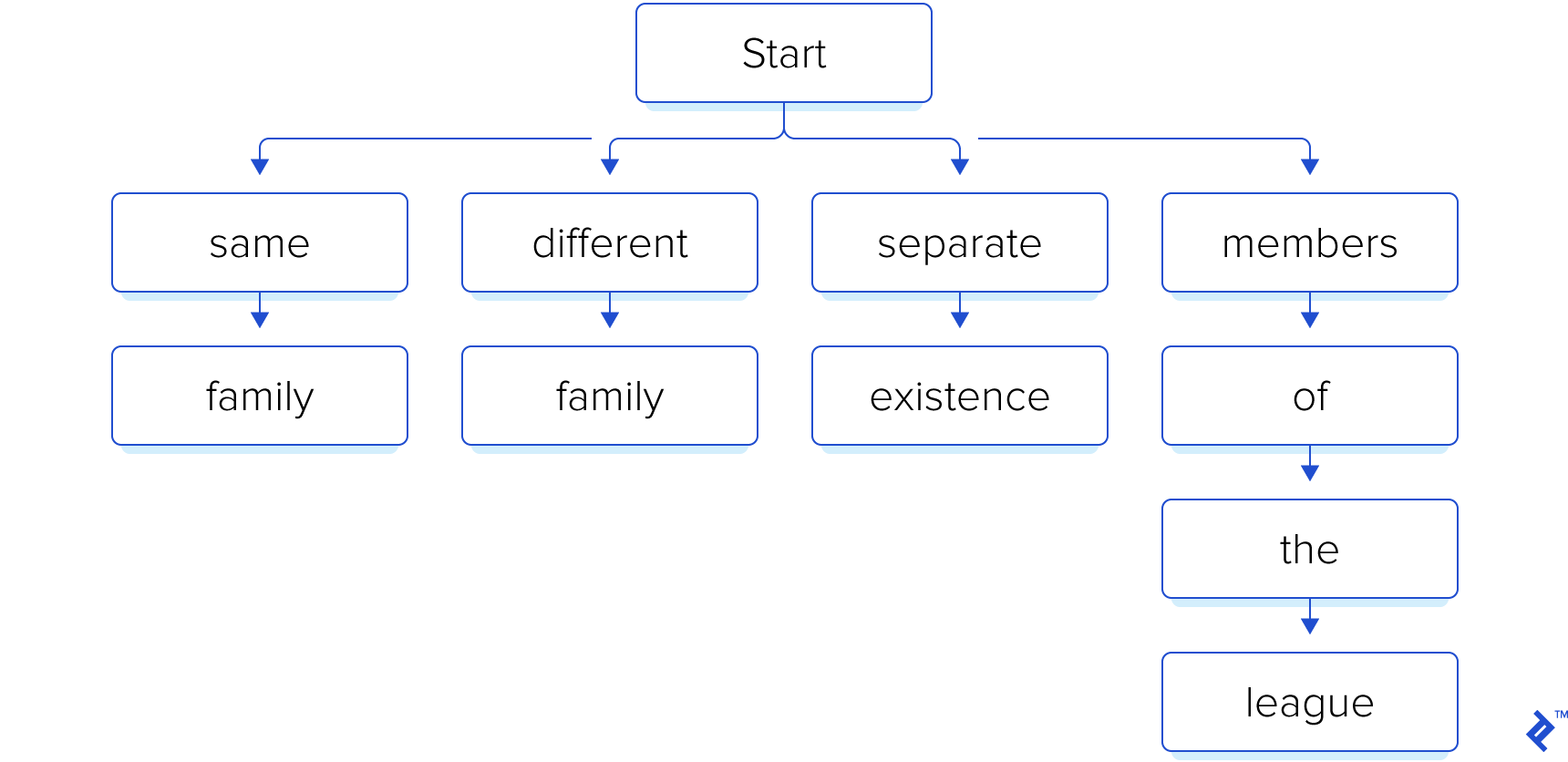
Later, the user of our software presents it with a file containing the following text:
The European languages are members of the same family. Their separate existence is a myth.
The rest is quite simple. Our algorithm will have two indicators (pointers, if you like), one starting at the root, or “start” node in our trie structure, and the other at the first word in the text body. The two indicators move along together, word by word. The text indicator simply moves forward, while the trie indicator traverses the trie depth-wise, following a trail of matching words.
The trie indicator returns to start in two cases: When it reaches the end of a branch, which means a search phrase has been found, or when it encounters a non-matching word, in which case no match has been found.
One exception to the movement of the text indicator is when a partial match is found, i.e. after a series of matches a non-match is encountered before the branch ends. In this case the text indicator is not moved forward, since the last word could be the beginning of a new branch.
Let’s apply this algorithm to our trie data structure example and see how it goes:
| Step | Trie Indicator | Text Indicator | Match? | Trie Action | Text Action |
|---|---|---|---|---|---|
| 0 | start | The | - | Move to start | Move to next |
| 1 | start | European | - | Move to start | Move to next |
| 2 | start | languages | - | Move to start | Move to next |
| 3 | start | are | - | Move to start | Move to next |
| 4 | start | members | members | Move to members | Move to next |
| 5 | members | of | of | Move to of | Move to next |
| 6 | of | the | the | Move to the | Move to next |
| 7 | the | same | - | Move to start | - |
| 8 | start | same | same | Move to same | Move to next |
| 9 | same | family | family | Move to start | Move to next |
| 10 | start | their | - | Move to start | Move to next |
| 11 | start | separate | separate | Move to separate | Move to next |
| 12 | separate | existence | existence | Move to start | Move to next |
| 13 | start | is | - | Move to start | Move to next |
| 14 | start | a | - | Move to start | Move to next |
| 15 | start | myth | - | Move to start | Move to next |
As we can see, the system successfully finds the two matching phrases, “same family” and “separate existence”.
Real-world Example
For a recent project, I was presented with the following problem: a client has a large number of articles and PhD theses relating to her field of work, and has generated her own list of phrases representing specific titles and rules relating to the same field of work.
Her dilemma was this: given her list of phrases, how does she link the articles/theses to those phrases? The end goal is to be able to randomly pick a group of phrases and immediately have a list of articles/theses that mention those particular phrases ready for grabbing.
As discussed previously, there are two parts to solving this problem: Indexing the phrases into a trie, and the actual search. The following sections provide a simple implementation in C#. Please note that file handling, encoding issues, text cleanup and similar problems are not handled in these snippets, since they are out of the scope of this article.
Indexing
The indexing operation simply traverses phrases one by one and inserts them into the trie, one word per node/level. Nodes are represented with the following class:
class Node
{
int PhraseId = -1;
Dictionary<String, Node> Children = new Dictionary<String, Node>();
public Node() { }
public Node(int id)
{
PhraseId = id;
}
}
Each phrase is represented by an ID, which can be as simple as an incremental number, and passed to the following indexing function (variable root is the actual root of the trie):
void addPhrase(ref Node root, String phrase, int phraseId)
{
// a pointer to traverse the trie without damaging
// the original reference
Node node = root;
// break phrase into words
String[] words = phrase.Split ();
// start traversal at root
for (int i = 0; i < words.Length; ++i)
{
// if the current word does not exist as a child
// to current node, add it
if (node.Children.ContainsKey(words[i]) == false)
node.Children.Add(words[i], new Node());
// move traversal pointer to current word
node = node.Children[words[i]];
// if current word is the last one, mark it with
// phrase Id
if (i == words.Length - 1)
node.PhraseId = phraseId;
}
}
Searching
The search process is a direct implementation of the trie algorithm discussed in the tutorial above:
void findPhrases(ref Node root, String textBody)
{
// a pointer to traverse the trie without damaging
// the original reference
Node node = root;
// a list of found ids
List<int> foundPhrases = new List<int>();
// break text body into words
String[] words = textBody.Split ();
// starting traversal at trie root and first
// word in text body
for (int i = 0; i < words.Length;)
{
// if current node has current word as a child
// move both node and words pointer forward
if (node.Children.ContainsKey(words[i]))
{
// move trie pointer forward
node = node.Children[words[i]];
// move words pointer forward
++i;
}
else
{
// current node does not have current
// word in its children
// if there is a phrase Id, then the previous
// sequence of words matched a phrase, add Id to
// found list
if (node.PhraseId != -1)
foundPhrases.Add(node.PhraseId);
if (node == root)
{
// if trie pointer is already at root, increment
// words pointer
++i;
}
else
{
// if not, leave words pointer at current word
// and return trie pointer to root
node = root;
}
}
}
// one case remains, word pointer as reached the end
// and the loop is over but the trie pointer is pointing to
// a phrase Id
if (node.PhraseId != -1)
foundPhrases.Add(node.PhraseId);
}
Performance
The code presented here is extracted from the actual project and has been simplified for the purpose of this document. Running this code again on the same machine [1] and against the same test sample [2] resulted in a runtime of 2.5 seconds for building the trie and 0.3 seconds for the search. So much for break time, eh?
Variations
It’s important to acknowledge that the algorithm as described in this trie tutorial can fail in certain edge cases, and therefore is designed with predefined search terms already in mind.
For example, if the beginning of one search term is identical to some part of another search term, as in:
- “to share and enjoy with friends”
- “I have two tickets to share with someone”
and the text body contains a phrase that causes the trie pointer to start down the wrong path, such as:
I have two tickets to share and enjoy with friends.
then the algorithm will fail to match any term, because the trie indicator will not return to the start node until the text indicator has already passed the beginning of the matching term in the text body.
It is important to consider whether this sort of edge case is a possibility for your application before implementing the algorithm. If so, the algorithm can be modified with additional trie indicators to track all of the matches at any given time, instead of just one match at a time.
Conclusion
Text search is a deep field in computer science; a field rich with problems and solutions alike. The kind of data I had to deal with (23MB of text is a ton of books in real life) might seem like a rare occurrence or a specialized problem, but developers who work with linguistics research, archiving, or any other type of data manipulation, come across much larger amounts of data on a regular basis.
As is evident in the trie data structure tutorial above, it is of great importance to carefully choose the correct algorithm for the problem at hand. In this particular case, the trie approach cut the runtime by a staggering 99.93%, from over an hour to less than 3 seconds.
By no means is this the only effective approach out there, but it is simple enough, and it works. I hope you have found this algorithm interesting, and wish you the best of luck in your coding endeavors.
[1] The machine used for this test has the following specs:
- Intel i7 4700HQ
- 16GB RAM
Testing was done on Windows 8.1 using .NET 4.5.1 and also Kubuntu 14.04 using the latest version of mono and the results were very similar.
[2] The test sample consists of 280K search phrases with a total size of 23.5MB, and a text body of 1.5MB.
Melbourne, Victoria, Australia
Member since June 11, 2014
About the author
Ahmed is an Android expert with a passion for intuitive user experience and snappy app performance.

