The Trie Data Structure: A Neglected Gem
From the very first days in our lives as programmers, we’ve all dealt with data structures: Arrays, linked lists, trees, sets, stacks and queues are our everyday companions, and the experienced programmer knows when and why to use them.
In this article we’ll see how an oft-neglected data structure, the trie, really shines in application domains with specific features, like word games.
From the very first days in our lives as programmers, we’ve all dealt with data structures: Arrays, linked lists, trees, sets, stacks and queues are our everyday companions, and the experienced programmer knows when and why to use them.
In this article we’ll see how an oft-neglected data structure, the trie, really shines in application domains with specific features, like word games.
When Anna started coding at a young age. Since then, her career has spanned many different projects and programming technologies.
From the very first days in our lives as programmers, we’ve all dealt with data structures: Arrays, linked lists, trees, sets, stacks and queues are our everyday companions, and the experienced programmer knows when and why to use them. In this article we’ll see how an oft-neglected data structure, the trie, really shines in application domains with specific features, like word games.
Word Games as Trie Example
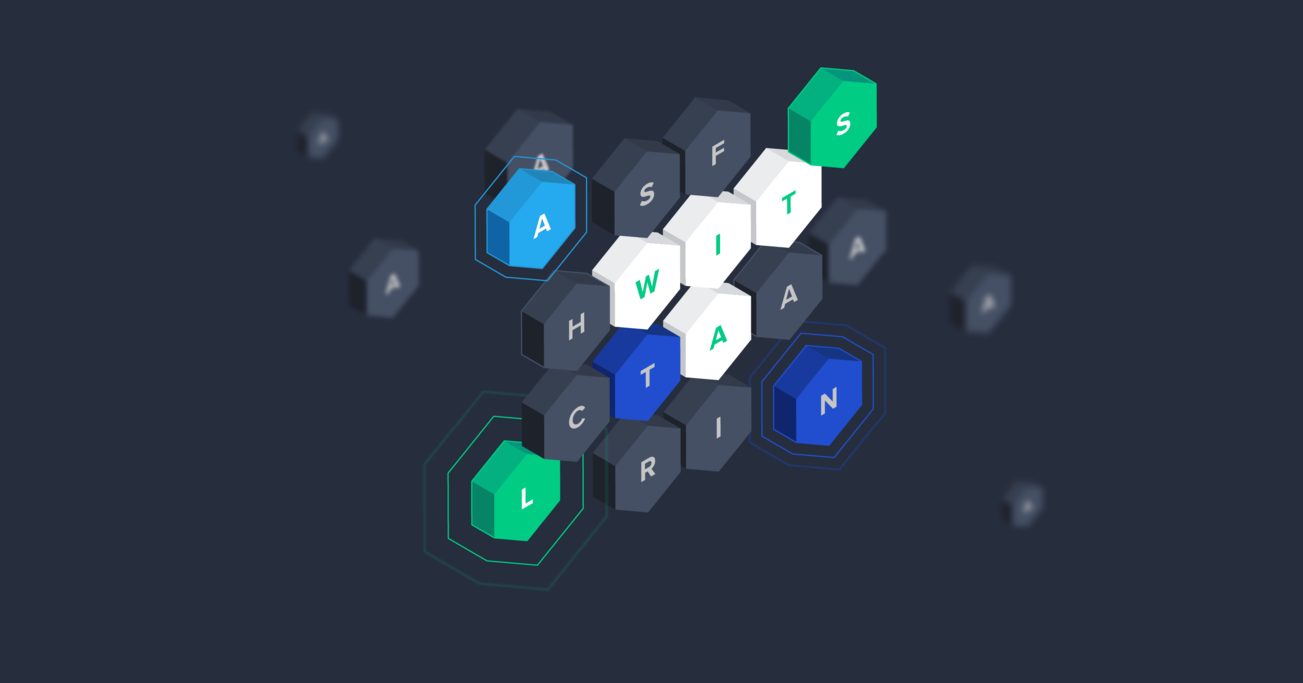
For starters, let’s consider a simple word puzzle: find all the valid words in a 4x4 letter board, connecting adjacent letters horizontally, vertically, or diagonally. For example, in the following board, we see the letters ‘W’, ‘A’, ‘I’, and ‘T’ connecting to form the word “WAIT”.

The naive solution to finding all valids words would be to explore the board starting from the upper-left corner and then moving depth-first to longer sequences, starting again from the second letter in the first row, and so on. In a 4x4 board, allowing vertical, horizontal and diagonal moves, there are 12029640 sequences, ranging in length from one to sixteen characters.
Now, our goal is to find the best data structure to implement this valid-word checker, i.e., our vocabulary. A few points to keep in mind:
- We only need a single copy of each word, i.e., our vocabulary is a set, from a logical point of view.
- We need to answer the following questions for any given word:
- Does the current character sequence comprise a valid word?
- Are there longer words that begin with this sequence? If not, we can abandon our depth-first exploration, as going deeper will not yield any valid words.
To illustrate the second point, consider the following board: There’s no point in exploring subsequent moves, since there are no words in the dictionary that start with “ASF”.

We’d love our data structure to answer these questions as quickly as possible. ~O(1) access time (for checking a sequence) would be ideal!
We can define the Vocabulary interface like this (see here for the GitHub repo):
public interface Vocabulary {
boolean add(String word);
boolean isPrefix(String prefix);
boolean contains(String word);
}
Trie Data Structure vs. Alternatives
Implementing the contains() method requires a backing data structure that lets you find elements efficiently, while the isPrefix() method requires us to find the “next greater element”, i.e. we need to keep the vocabulary sorted in some way.
We can easily exclude hash-based sets from our list of candidates: while such a structure would give us constant-time checking for contains(), it would perform quite poorly on isPrefix(), in the worst case requiring that we scan the whole set.
For quite the opposite reason, we can also exclude sorted linked-lists, as they require scanning the list at least up to the first element that is greater than or equal to the searched word or prefix.
Two valid options are using a sorted array-backed list or a binary tree.
On the sorted array-backed list we can use binary search to find the current sequence if present or the next greater element at a cost of O(log2(n)), where n is the number of words in the dictionary.
We can implement an array-backed vocabulary that always maintains ordering of like this, using standard java.util.ArrayList and java.util.Collections.binarySeach:
public class ListVocabulary implements Vocabulary {
private List<String> words = new ArrayList<String>();
/**
* Constructor that adds all the words and then sorts the underlying list
*/
public ListVocabulary(Collection<String> words) {
this.words.addAll(words);
Collections.sort(this.words);
}
public boolean add(String word) {
int pos = Collections.binarySearch(words, word);
// pos > 0 means the word is already in the list. Insert only
// if it's not there yet
if (pos < 0) {
words.add(-(pos+1), word);
return true;
}
return false;
}
public boolean isPrefix(String prefix) {
int pos = Collections.binarySearch(words, prefix) ;
if (pos >= 0) {
// The prefix is a word. Check the following word, because we are looking
// for words that are longer than the prefix
if (pos +1 < words.size()) {
String nextWord = words.get(pos+1);
return nextWord.startsWith(prefix);
}
return false;
}
pos = -(pos+1);
// The prefix is not a word. Check where it would be inserted and get the next word.
// If it starts with prefix, return true.
if (pos == words.size()) {
return false;
}
String nextWord = words.get(pos);
return nextWord.startsWith(prefix);
}
public boolean contains(String word) {
int pos = Collections.binarySearch(words, word);
return pos >= 0;
}
}
If we decided to use a binary tree, the implementation could be even shorter and more elegant (again, here’s a link to the code):
public class TreeVocabulary extends TreeSet<String> implements Vocabulary {
public TreeVocabulary(Collection<String> c) {
super(c);
}
public boolean isPrefix(String prefix) {
String nextWord = ceiling(prefix);
if (nextWord == null) {
return false;
}
if (nextWord.equals(prefix)) {
Set<String> tail = tailSet(nextWord, false);
if (tail.isEmpty()) {
return false;
}
nextWord = tail.iterator().next();
}
return nextWord.startsWith(prefix);
}
/**
* There is a mismatch between the parameter types of vocabulary and TreeSet, so
* force call to the upper-class method
*/
public boolean contains(String word) {
return super.contains(word);
}
}
In both cases, we can expect O(log n) performance for each access method (contains() and isPrefix()). As for space requirements, both the array-backed implementation and the tree-backed implementation require O(n+M) where n is the number of words in the dictionary and M is the bytesize of the dictionary, i.e. the sum of the length of the strings in the dictionary.
Trie Applications: When and Why Use Tries
Logarithmic performance and linear memory isn’t bad. But there are a few more characteristics of our application domain that can lead us to better performance:
- We can safely assume that all words are lowercase.
- We accept only a-z letters—no punctuation, no hyphens, no accents, etc.
- The dictionary contains many inflected forms: plurals, conjugated verbs, composite words (e.g., house –> housekeeper). Therefore, many words share the same stem.
- Words have a limited length. For example, if we are working on a 4x4 board, all words longer than 16 chars can be discarded.
This is where the trie (pronounced “try”) comes in. But what exactly is a trie? Tries are neglected data structures, found in books but rarely in standard libraries.
For motivation, let’s first consider Computer Science’s poster child: the binary tree. Now, when we analyze the performance of a binary tree and say operation x is O(log(n)), we’re constantly talking log base 2. But what if, instead of a binary tree, we used a ternary tree, where every node has three children (or, a fan-out of three). Then, we’d be talking log base 3. (That’s a performance improvement, albeit only by a constant factor.) Essentially, our trees would become wider but shorter, and we could perform fewer lookups as we don’t need to descend quite so deep.
Taking things a step further, what if we had a tree with fan-out equal to the number of possible values of our datatype?
This is the motivation behind the trie. And as you may have guessed, a trie is indeed a tree, a trie tree so to speak!
But, contrary to most binary-trees that you’d use for sorting strings, those that would store entire words in their nodes, each node of a trie holds a single character (and not even that, as we’ll see soon) and has a maximum fan-out equal to the length of the alphabet. In our case, the length of the alphabet is 26; therefore the nodes of the trie have a maximum fan-out of 26. And, while a balanced binary tree has log2(n) depth, the maximum depth of the trie is equal to the maximum length of a word! (Again, wider but shorter.)
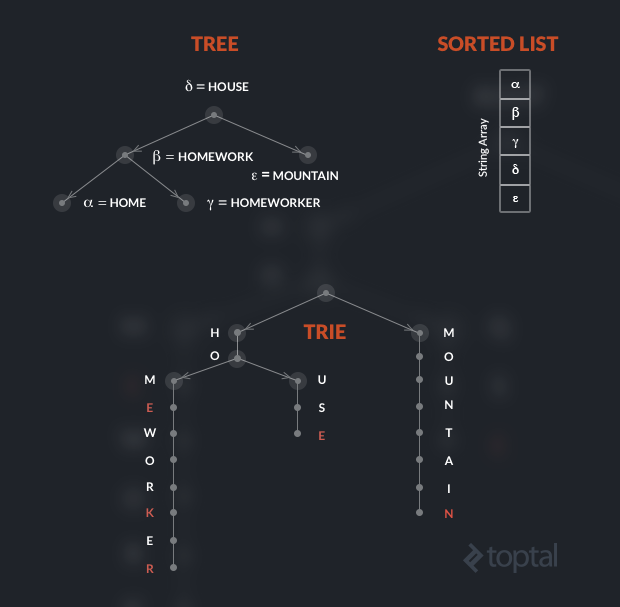
Within a trie, words with the same stem (prefix) share the memory area that corresponds to the stem.
To visualize the difference, let’s consider a small dictionary made of five words. Assume that the Greek letters indicate pointers, and note that in the trie, red characters indicate nodes holding valid words.
Java Trie Implementation
As we know, in the tree the pointers to the children elements are usually implemented with a left and right variable, because the maximum fan-out is fixed at two.
In a trie indexing an alphabet of 26 letters, each node has 26 possible children and, therefore, 26 possible pointers. Each node thus features an array of 26 (pointers to) sub-trees, where each value could either be null (if there is no such child) or another node.
How, then, do we look-up a word in a trie? Here is the method that, given a String s, will identify the node that corresponds to the last letter of the word, if it exists in the tree:
public LowercaseTrieVocabulary getNode(String s) {
LowercaseTrieVocabulary node = this;
for (int i = 0; i < s.length(); i++) {
int index = LOWERCASE.getIndex(s.charAt(i));
LowercaseTrieVocabulary child = node.children[index];
if (child == null) {
// There is no such word
return null;
}
node = child;
}
return node;
}
The LOWERCASE.getIndex(s.charAt(i)) method simply returns the position of the ith character in the alphabet. On the returned node, a Boolean property node indicates that the node corresponds to the last letter of a word, i.e. a letter marked in red in the previous example. Since each node keeps a counter of the number of children, if this counter is positive then there are longer words in the dictionary that have the current string as a prefix. Note: the node does not really need to keep a reference to the character that it corresponds to, because it’s implicit in its position in the trie.
Analyzing Performance
What makes the trie structure really perform well in these situations is that the cost of looking up a word or prefix is fixed and dependent only on the number of characters in the word and not on the size of the vocabulary.
In our specific domain, since we have strings that are at most 16 characters, exactly 16 steps are necessary to find a word that is in the vocabulary, while any negative answer, i.e. the word or prefix is not in the trie, can be obtained in at most 16 steps as well! Considering that we have previously ignored the length of the string when calculating running time complexity for both the array-backed sorted list and the tree, which is hidden in the string comparisons, we can as well ignore it here and safely state that lookup is done in O(1) time.
Considering space requirements (and remembering that we have indicated with M the bytesize of the dictionary), the trie could have M nodes in the worst case, if no two strings shared a prefix. But since we have observed that there is high degree of redundancy in the dictionary, there is a lot of compression to be done. The English dictionary that is used in the example code is 935,017 bytes and requires 250,264 nodes, with a compression ratio of about 73%.
However, despite this, even a compressed trie will usually require more memory than a tree or array. This is because, for each node, at least 26 x sizeof(pointer) bytes are necessary, plus some overhead for the object and additional attributes. On a 64-bit machine, each node requires more than 200 bytes, whereas a string character requires a single byte, or two if we consider UTF strings.
Tries and Performance Tests
So, what about performance? The vocabulary implementations were tested in two different situations: checking for 20,000,000 random strings and finding all the words in 15,000 boards randomly generated from the same word list.
Four data structures were analyzed: an array-backed sorted list, a binary tree, the trie described above, and a trie using arrays of bytes corresponding to the alphabet-index of the characters themselves (a minor and easily implemented performance optimization). Here are the results, in ms:
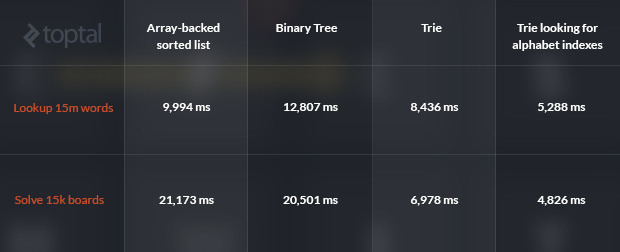
The average number of moves made to solve the board is 2,188. For each move, a word lookup and a prefix lookup are done, i.e., for checking all the boards, more than 32M word lookups and 32M prefix lookups were performed. Note: these could be done in a single step, I kept them separated for clarity in the exposition. Compacting them in a single step would cut the time for solving the boards almost in half, and would probably favour the trie even more.
As can be seen above, the word lookup perform better with the trie even when using strings, and is even faster when using alphabet indexes, with the latter performing more than twice as fast as a standard binary tree. The difference in solving the boards is even more evident, with the fast trie-alphabet-index solution being more than four times as fast as the list and the tree.
Wrapping Up
The trie is a very specialized data structure that requires much more memory than trees and lists. However, when specific domain characteristics apply, like a limited alphabet and high redundancy in the first part of the strings, it can be very effective in addressing performance optimization.
References
An extensive explanation of tries and alphabets can be found in chapter 5 of Robert Sedgewick’s book “Algorithms, 4th edition”. The companion website at Princeton has the code for an implementation of Alphabet and TrieST that is more extensive than my example.
Description of the trie and implementations for various languages can also be found on Wikipedia and you can take a look at this Boston University trie resource as well.
Further Reading on the Toptal Blog:
Understanding the basics
What is a trie?
A trie is an ordered data structure, a type of search tree used to store associative data structures. It is also referred to as a Radix tree or Prefix tree.
What is a compressed trie?
A compressed trie is essentially a trie data structure with an additional rule that every node has to have two or more children.
Which trie pronunciation is correct?
A trie is pronounced “try,” although the name trie is derived from “retrieval.”
What is a trie data structure good for?
The trie data structure is well-suited to matching algorithms, as they are based on the prefix of each string. Tries are typically employed when dealing with groups of strings rather than individual strings, enabling them to solve a wide range of problems.
About the author
When Anna started coding at a young age. Since then, her career has spanned many different projects and programming technologies.