How to Use Rails Helpers: A Bootstrap Carousel Demonstration
One of the most misused, misunderstood, and neglected of all the Rails built-in structures is the view helper. Helpers often get a bad reputation for being a dumping ground for one-off methods used across the entire application’s view layer. But what if your helpers could be more semantic, better organized, and even reusable across projects? What if they could be more than just one-off functions sprinkled throughout the view, but powerful methods that generated complex markup with ease leaving your views free of conditional logic and code?
Let’s see how to do this when building an image carousel, with the familiar Twitter Bootstrap framework and some good old-fashioned object-oriented programming.
One of the most misused, misunderstood, and neglected of all the Rails built-in structures is the view helper. Helpers often get a bad reputation for being a dumping ground for one-off methods used across the entire application’s view layer. But what if your helpers could be more semantic, better organized, and even reusable across projects? What if they could be more than just one-off functions sprinkled throughout the view, but powerful methods that generated complex markup with ease leaving your views free of conditional logic and code?
Let’s see how to do this when building an image carousel, with the familiar Twitter Bootstrap framework and some good old-fashioned object-oriented programming.
Carlos is a professional software engineer specializing in the Ruby on Rails framework. He has worked with US tech companies for years.
Expertise
One of the most misused, misunderstood, and neglected of all the Rails built-in structures is the view helper. Located in your app/helpers directory and generated by default with every new Rails project, helpers often get a bad reputation for being a dumping ground for one-off methods used across the entire application’s view layer. Unfortunately, Rails itself encourages this lack of structure and poor organization by including all helpers into every view by default, creating a polluted global namespace.
But what if your helpers could be more semantic, better organized, and even reusable across projects? What if they could be more than just one-off functions sprinkled throughout the view, but powerful methods that generated complex markup with ease leaving your views free of conditional logic and code?
Let’s see how to do this when building an image carousel, with the familiar Twitter Bootstrap framework and some good old-fashioned object-oriented programming.
When to use Rails helpers
There are many different design patterns that can be used in Rails’ view layer: presenters, decorators, partials, as well as helpers, just to name a few. My simple rule of thumb is that helpers work great when you want to generate HTML markup that requires a certain structure, specific CSS classes, conditional logic, or reuse across different pages.
The best example of the power of Rails helpers is demonstrated by the FormBuilder with all its associated methods for generating input fields, select tags, labels, and other HTML structures. These helpful methods generate markup for you with the all the relevant attributes set properly. Convenience like this is why we all fell in love with Rails in the first place.
The benefits of using well-crafted helpers is the same as any well-written, clean code: encapsulation, reduction of code repetition (DRY), and keeping logic out of the view.
Anatomy of a Twitter Bootstrap Carousel
Twitter Bootstrap is a widely used front-end framework that comes with built-in support for common components such as modals, tabs, and image carousels. These Bootstrap components are a great use case for custom helpers because the markup is highly structured, requires certain classes, IDs, and data attributes to be set correctly for the JavaScript to work, and setting those attributes requires a bit of conditional logic.
A Bootstrap 3 carousel has the following markup:
<div id="carousel-example-generic" class="carousel slide" data-ride="carousel">
<!-- Indicators -->
<ol class="carousel-indicators">
<li data-target="#carousel-example-generic" data-slide-to="0" class="active"></li>
<li data-target="#carousel-example-generic" data-slide-to="1"></li>
<li data-target="#carousel-example-generic" data-slide-to="2"></li>
</ol>
<!-- Wrapper for slides -->
<div class="carousel-inner">
<div class="item active">
<img src="..." alt="...">
</div>
<div class="item">
<img src="..." alt="...">
</div>
...
</div>
<!-- Controls -->
<a class="left carousel-control" href="#carousel-example-generic" data-slide="prev">
<span class="glyphicon glyphicon-chevron-left"></span>
</a>
<a class="right carousel-control" href="#carousel-example-generic" data-slide="next">
<span class="glyphicon glyphicon-chevron-right"></span>
</a>
</div>
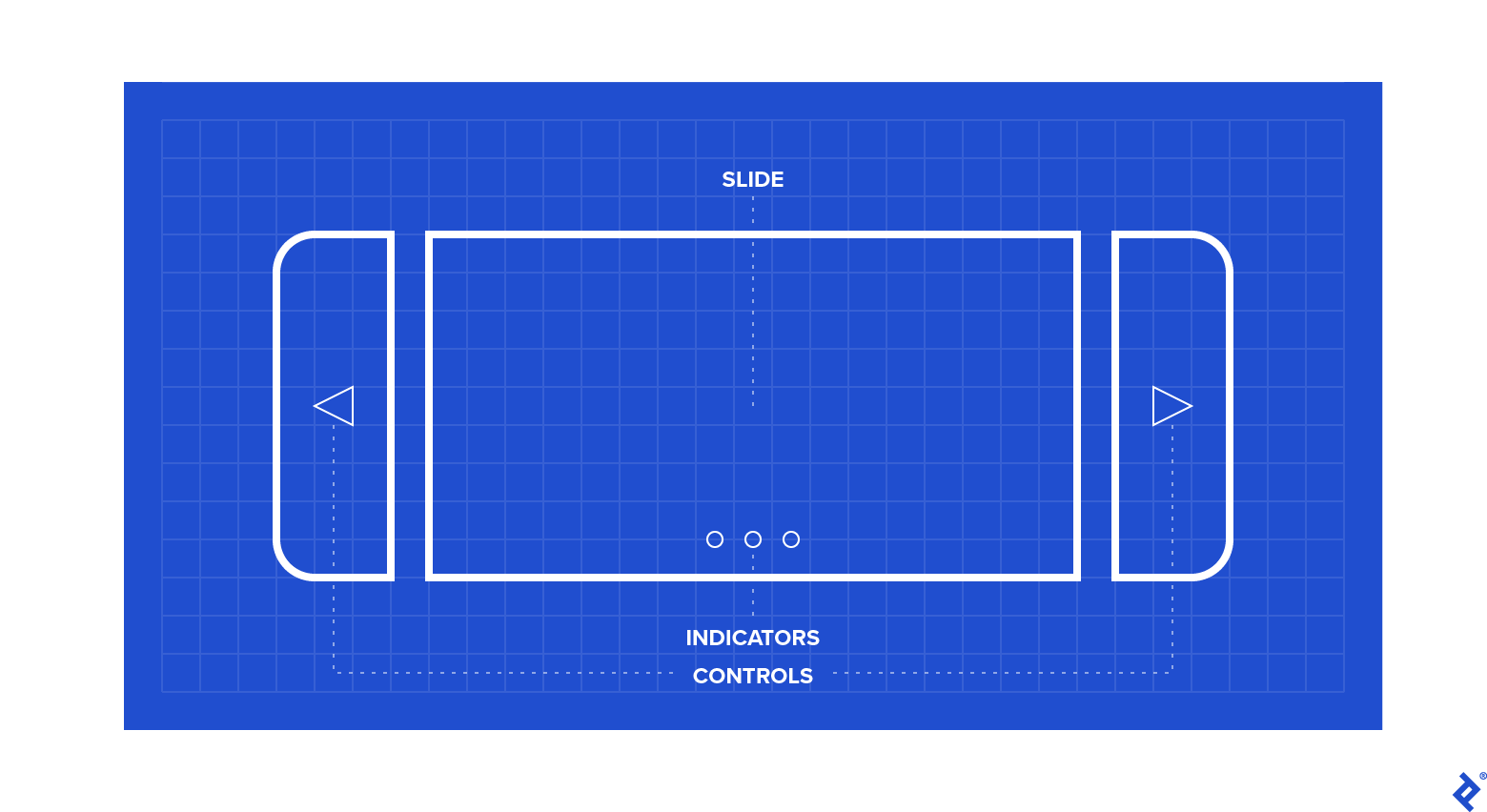
As you can see, there are three main structures: (1) the indicators (2) the image slides (3) the slide controls.
The goal is to be able to build a single helper method that takes a collection of images and renders this entire carousel component, ensuring that data, id, href attributes and CSS classes are all set properly.
The Helper
Let’s start with a basic outline of the helper:
# app/helpers/carousel_helper.rb
module CarouselHelper
def carousel_for(images)
Carousel.new(self, images).html
end
class Carousel
def initialize(view, images)
@view, @images = view, images
end
def html
# TO FILL IN
end
private
attr_accessor :view, :images
end
end
The helper method carousel_for will return the complete carousel markup for the given image URLs. Rather than building out a suite of individual methods to render each portion of the carousel (which would require us passing around the image collection and other stateful information to each method), we’ll create a new plain-old-Ruby class called Carousel to represent the carousel data. This class will expose an html method which returns the fully rendered markup. We initialize it with the collection of image URLs images, and the view context view.
Note that the view parameter is an instance of ActionView, which all Rails helpers are mixed into. We pass it along to our object instance in order to gain access to Rails’ built-in helper methods such as link_to, content_tag, image_tag, and safe_join, which we will be using to build out the markup within the class.
We’ll also add the delegate macro, so we can call those methods directly, without referring to view:
def html
content = view.safe_join([indicators, slides, controls])
view.content_tag(:div, content, class: 'carousel slide')
end
private
attr_accessor :view, :images
delegate :link_to, :content_tag, :image_tag, :safe_join, to: :view
def indicators
# TO FILL IN
end
def slides
# TO FILL IN
end
def controls
# TO FILL IN
end
We know that a carousel is comprised of three separate components, so let’s stub out methods which will eventually give us the markup for each, then have the html method join them into a container div tag, applying the necessary Bootstrap classes for the carousel itself.
safe_join is a handy built-in method which concatenates a collection of strings together and calls html_safe on the result. Remember, we have access to those methods via the view parameter, which we passed in when we created the instance.
We’ll build out the indicators first:
def indicators
items = images.count.times.map { |index| indicator_tag(index) }
content_tag(:ol, safe_join(items), class: 'carousel-indicators')
end
def indicator_tag(index)
options = {
class: (index.zero? ? 'active' : ''),
data: {
target: uid,
slide_to: index
}
}
content_tag(:li, '', options)
end
The indicators are a simple ordered list ol that has a list item li element for each image in the collection. The currently active image indicator needs the active CSS class, so we’ll make sure that it’s set for the first indicator we create. This is a great example of logic which would normally have to be in the view itself.
Notice that the indicators need to reference the unique id of the containing carousel element (in case there is more than one carousel on the page). We can easily generate this id in the initializer and use it throughout the rest of the class (specifically within the indicators and the controls). Doing this programmatically inside a helper method ensures that the id will be consistent across carousel elements. There are many times when a small typo or changing the id in one place but not the others will cause a carousel to break; that won’t happen here because all the elements automatically reference the same id.
def initialize(view, images)
# ...
@uid = SecureRandom.hex(6)
end
attr_accessor :uid
Next up are the image slides:
def slides
items = images.map.with_index { |image, index| slide_tag(image, index.zero?) }
content_tag(:div, safe_join(items), class: 'carousel-inner')
end
def slide_tag(image, is_active)
options = {
class: (is_active ? 'item active' : 'item'),
}
content_tag(:div, image_tag(image), options)
end
We simply iterate over each of the images that we passed to the Carousel instance and create the proper markup: an image tag wrapped in a div with the item CSS class, again making sure to add the active class to the first one we create.
Lastly, we need the Previous/Next controls:
def controls
safe_join([control_tag('left'), control_tag('right')])
end
def control_tag(direction)
options = {
class: "#{direction} carousel-control",
data: { slide: direction == 'left' ? 'prev' : 'next' }
}
icon = content_tag(:i, nil, class: "glyphicon glyphicon-chevron-#{direction}")
control = link_to(icon, "##{uid}", options)
end
We create links that control the carousel’s movement back and forth between images. Note the usage of uid again; no need to worry about not using the right ID in all the different places within the carousel structure, it’s automatically consistent and unique.
The finished product:
With that, our carousel helper is complete. Here it is in its entirety:
# app/helpers/carousel_helper.rb
module CarouselHelper
def carousel_for(images)
Carousel.new(self, images).html
end
class Carousel
def initialize(view, images)
@view, @images = view, images
@uid = SecureRandom.hex(6)
end
def html
content = safe_join([indicators, slides, controls])
content_tag(:div, content, id: uid, class: 'carousel slide')
end
private
attr_accessor :view, :images, :uid
delegate :link_to, :content_tag, :image_tag, :safe_join, to: :view
def indicators
items = images.count.times.map { |index| indicator_tag(index) }
content_tag(:ol, safe_join(items), class: 'carousel-indicators')
end
def indicator_tag(index)
options = {
class: (index.zero? ? 'active' : ''),
data: {
target: uid,
slide_to: index
}
}
content_tag(:li, '', options)
end
def slides
items = images.map.with_index { |image, index| slide_tag(image, index.zero?) }
content_tag(:div, safe_join(items), class: 'carousel-inner')
end
def slide_tag(image, is_active)
options = {
class: (is_active ? 'item active' : 'item'),
}
content_tag(:div, image_tag(image), options)
end
def controls
safe_join([control_tag('left'), control_tag('right')])
end
def control_tag(direction)
options = {
class: "#{direction} carousel-control",
data: { slide: direction == 'left' ? 'prev' : 'next' }
}
icon = content_tag(:i, '', class: "glyphicon glyphicon-chevron-#{direction}")
control = link_to(icon, "##{uid}", options)
end
end
end
The helper in action:
Finally, to drive home the point, let’s look at a quick example of how this helper can make our lives easier. Say we are building a website for apartment rental listings. Each Apartment object has a list of the image URLs:
class Apartment
def image_urls
# ...
end
end
With our carousel helper, we can render the entire Bootstrap carousel with a single call to carousel_for, completely removing the fairly-complex logic from the view:
<% apartment = Apartment.new %>
# ...
<%= carousel_for(apartment.image_urls) %>
Not sure when to use Rails view helpers? Here's a demonstration.
Conclusion
Using this simple, yet powerful, technique, we’ve moved what would be a significant amount of markup and logic out of the view layer and into a helper function that can be used to render carousel components anywhere with just a carousel_for(some_images) call. This generic helper can be used across all your Rails projects whenever you are using Twitter Bootstrap. Most importantly, you now have a new tool in your toolkit that you can use for project-specific components, too.
So, the next time you find yourself typing and retyping the same kind of markup and embedding conditional logic into your views, see if a helper function is just waiting to be written to make your life easier.
San Rafael, CA, United States
Member since December 6, 2014
About the author
Carlos is a professional software engineer specializing in the Ruby on Rails framework. He has worked with US tech companies for years.