Stork, Part 2: Creating an Expression Parser
Would you rather develop a statically or dynamically typed programming language? How would you devise your expression parser?
In the second part of our Stork series, Toptal Full-stack Developer Jakisa Tomic outlines his preferred approach and demonstrates how you can create a functional expression parser.
Would you rather develop a statically or dynamically typed programming language? How would you devise your expression parser?
In the second part of our Stork series, Toptal Full-stack Developer Jakisa Tomic outlines his preferred approach and demonstrates how you can create a functional expression parser.
Jakisa has 15+ years of experience developing various apps on multiple platforms. Most of his technical expertise is in C++ development.
Expertise
PREVIOUSLY AT

In this part of our series, we will cover one of the trickier (at least in my opinion) components of scripting a language engine, which is an essential building block for every programming language: the expression parser.
A question that a reader could ask—and rightfully so—is: Why don’t we simply use some sophisticated tools or libraries, something already at our disposal?
Why don’t we use Lex, YACC, Bison, Boost Spirit, or at least regular expressions?
Throughout our relationship, my wife has noticed a trait of mine that I cannot deny: Whenever faced with a difficult question, I make a list. If you think about it, it makes perfect sense—I am using quantity to compensate for the lack of quality in my answer.
I will do the same thing now.
- I want to use standard C++. In this case, that will be C++17. I think the language is quite rich on its own, and I am fighting the urge to add anything but the standard library into the mix.
- When I developed my first scripting language, I didn’t use any sophisticated tools. I was under pressure and on a tight deadline, yet I didn’t know how to use Lex, YACC, or anything similar. Therefore, I decided to develop everything manually.
- Later, I found a blog by an experienced programming language developer, who advised against using any of these tools. He said those tools solve the easier part of language development, so in any case, you are left with the difficult stuff. I cannot find that blog right now, as it was long ago, when both the internet and I were young.
- At the same time, there was a meme that said: “You have a problem which you decide to solve by using regular expressions. Now you have two problems.”
- I don’t know Lex, YACC, Bison, or anything similar. I know Boost Spirit, and it is a handy and amazing library, but I still prefer to have better control over the parser.
- I like to do those components manually. Actually, I could just give this answer and remove this list completely.
The full code is available at my GitHub page.
Token Iterator
There are some changes to the code from Part 1.
These are mostly simple fixes and small changes, but one important addition to the existing parsing code is the class token_iterator. It allows us to evaluate the current token without removing it from the stream, which is really handy.
class tokens_iterator {
private:
push_back_stream& _stream;
token _current;
public:
tokens_iterator(push_back_stream& stream);
const token& operator*() const;
const token* operator->() const;
tokens_iterator& operator++();
explicit operator bool() const;
};
It is initialized with push_back_stream, and then it can be dereferenced and incremented. It can be checked with explicit bool cast, which will evaluate to false when the current token is equal to eof.
Statically or Dynamically Typed Language?
There is one decision that I have to make in this part: Will this language be statically or dynamically typed?
A statically typed language is a language that checks the types of its variables at the time of compilation.
A dynamically typed language, on the other hand, doesn’t check it during the compilation (if there is a compilation, which is not mandatory for a dynamically typed language) but during the execution. Therefore, potential errors can live in the code until they are hit.
This is an obvious advantage of statically typed languages. Everybody likes to catch their errors as soon as possible. I always wondered what the biggest advantage of dynamically typed languages is, and the answer struck me in the last couple of weeks: It is much easier to develop!
The previous language that I developed was dynamically typed. I was more or less satisfied with the result, and writing the expression parser wasn’t too difficult. You basically don’t have to check variable types and you rely on runtime errors, which you code almost spontaneously.
For example, if you have to write the binary + operator and you want to do it for numbers, you just need to evaluate both sides of that operator as numbers in the runtime. If either of the sides cannot evaluate the number, you just throw an exception. I’ve even implemented operator overloading by checking the runtime type information of variables in an expression, and operators were part of that runtime information.
In the first language I developed (this is my third one), I did type checking at the time of compilation, but I hadn’t taken full advantage of that. Expression evaluation was still depending on the runtime type information.
Now, I decided to develop a statically typed language, and it turned out to be a much harder task than expected. However, since I don’t plan to compile it to a binary, or any kind of emulated assembly code, some type of information will implicitly exist in the compiled code.
Types
As a bare minimum of types that we have to support, we will start with the following:
- Numbers
- Strings
- Functions
- Arrays
Although we may add them going forward, we will not support structures (or classes, records, tuples, etc.) at the beginning. However, we will keep in mind that we may add them later, so we will not seal our fate with decisions that are hard to change.
First, I wanted to define the type as a string, which will follow some convention. Every identifier would keep that string by value at the time of compilation, and we will have to parse it sometimes. For example, if we encode the type of array of numbers as “[number],” then we will have to trim the first and the last character in order to get an inner type, which is “number” in this case. It’s a pretty bad idea if you think about it.
Then, I tried to implement it as a class. That class would have all the information about the type. Each identifier would keep a shared pointer to that class. In the end, I thought about having the registry of all types used during the compilation, so each identifier would have the raw pointer to its type.
I liked that idea, so we ended up with the following:
using type = std::variant<simple_type, array_type, function_type>;
using type_handle = const type*;
Simple types are members of the enum:
enum struct simple_type {
nothing,
number,
string,
};
Enumeration member nothing is here as a placeholder for void, which I cannot use as it is a keyword in C++.
Array types are represented with the structure having the sole member of type_handle.
struct array_type {
type_handle inner_type_id;
};
Obviously, the array length is not part of array_type, so arrays will grow dynamically. That means that we will end up with std::deque or something similar, but we will deal with that later.
A function type is composed of its return type, type of each of its parameters, and whether or not each of those parameters is passed by value or by reference.
struct function_type {
struct param {
type_handle type_id;
bool by_ref;
};
type_handle return_type_id;
std::vector<param> param_type_id;
};
Now, we can define the class that will keep those types.
class type_registry {
private:
struct types_less{
bool operator()(const type& t1, const type& t2) const;
};
std::set<type, types_less> _types;
static type void_type;
static type number_type;
static type string_type;
public:
type_registry();
type_handle get_handle(const type& t);
static type_handle get_void_handle() {
return &void_type;
}
static type_handle get_number_handle() {
return &number_type;
}
static type_handle get_string_handle() {
return &string_type;
}
};
Types are kept in std::set, as that container is stable, meaning that pointers to its members are valid even after new types are inserted. There is the function get_handle, which registers passed type and returns the pointer to it. If the type is already registered, it will return the pointer to the existing type. There are also convenience functions to get primitive types.
As for implicit conversion between types, numbers will be convertible to strings. It shouldn’t be dangerous, as a reverse conversion is not possible, and the operator for string concatenation is distinctive to the one for number addition. Even if that conversion is removed in the later stages of the development of this language, it will serve well as an exercise at this point. For that purpose, I had to modify the number parser, as it always parsed . as a decimal point. It may be the first character of the concatenation operator ...
Compiler Context
During compilation, different compiler functions need to get information about the code compiled so far. We will keep that information in a class compiler_context. Since we are about to implement expression parsing, we will need to retrieve information about the identifiers that we encounter.
During the runtime, we will keep variables in two different containers. One of them will be the global variable container, and another will be the stack. The stack will grow as we call functions and enter scopes. It will shrink as we return from functions and leave scopes. When we call some function, we will push function parameters, and then the function will execute. Its return value will be pushed to the top of the stack when it leaves. Therefore, for each function, the stack will look like this:
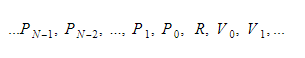
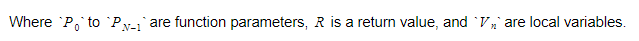
The function will keep the absolute index of the return variable, and each variable or parameter will be found relative to that index.
For now, we will treat functions as constant global identifiers.
This is the class that serves as identifier information:
class identifier_info {
private:
type_handle _type_id;
size_t _index;
bool _is_global;
bool _is_constant;
public:
identifier_info(type_handle type_id, size_t index,
bool is_global, bool is_constant);
type_handle type_id() const;
size_t index() const;
bool is_global() const;
bool is_constant() const;
};
For local variables and function parameters, function index returns the index relative to the return value. It returns the absolute global index in case of global identifiers.
We will have three different identifier lookups in compile_context:
- Global identifier lookup, which will
compile_contexthold by value, as it is the same throughout the whole compilation. - Local identifier lookup, as a
unique_ptr, which will benullptrin the global scope and will be initialized in any function. Whenever we enter the scope, the new local context will be initialized with the old one as its parent. When we leave the scope, it will be replaced by its parent. - Function identifier lookup, which will be the raw pointer. It will be
nullptrin global scope, and the same value as the outermost local scope in any function.
class compiler_context {
private:
global_identifier_lookup _globals;
function_identifier_lookup* _params;
std::unique_ptr<local_identifier_lookup> _locals;
type_registry _types;
public:
compiler_context();
type_handle get_handle(const type& t);
const identifier_info* find(const std::string& name) const;
const identifier_info* create_identifier(std::string name,
type_handle type_id, bool is_constant);
const identifier_info* create_param(std::string name,
type_handle type_id);
void enter_scope();
void enter_function();
bool leave_scope();
};
Expression Tree
When expression tokens are parsed, they are converted to an expression tree. Similar to all trees, this one also consists of nodes.
There are two different kinds of nodes:
- Leaf nodes, which can be:
a) Identifiers
b) Numbers
c) Strings - Inner nodes, which represent an operation on their child nodes. It keeps its children with
unique_ptr.
For each node, there is information about its type and whether or not it returns an lvalue (a value that can appear on the left side of = operator).
When an inner node is created, it will try to convert return types of its children to types that it expects. The following implicit conversions are allowed:
- lvalue to non-lvalue
- Anything to
void -
numbertostring
If the conversion is not allowed, a semantic error will be thrown.
Here is the class definition, without some helper functions and implementation details:
enum struct node_operation {
...
};
using node_value = std::variant<
node_operation,
std::string,
double,
identifier
>;
struct node {
private:
node_value _value;
std::vector<node_ptr> _children;
type_handle _type_id;
bool _lvalue;
public:
node(
compiler_context& context,
node_value value,
std::vector<node_ptr> children
);
const node_value& get_value() const;
const std::vector<node_ptr>& get_children() const;
type_handle get_type_id() const;
bool is_lvalue() const;
void check_conversion(type_handle type_id, bool lvalue);
};
The functionality of methods is self-explanatory, except for the function check_conversion. It will check if the type is convertible to the passed type_id and boolean lvalue by obeying type conversion rules and will throw an exception if it is not.
If a node is initialized with std::string, or double, its type will be string or number, respectively, and it will not be an lvalue. If it is initialized with an identifier, it will assume the type of that identifier and will be an lvalue if the identifier is not constant.
If it is initialized, however, with a node operation, its type will depend on the operation, and sometimes on the type of its children. Let’s write the expression types in the table. I will use & suffix to denote an lvalue. In cases when multiple expressions have the same treatment, I will write additional expressions in round brackets.
Unary Operations
| Operation | Operation type | x type |
| ++x (--x) | number& | number& |
| x++ (x--) | number | number& |
| +x (-x ~x !x) | number | number |
Binary Operations
| Operation | Operation type | x type | y type |
| x+y (x-y x*y x/y x\y x%y x&y x|y x^y x<<y x>>y x&&y x||y) | number | number | number |
| x==y (x!=y x<y x>y x<=y x>=y) | number | number or string | same as x |
| x..y | string | string | string |
| x=y | same as x | lvalue of anything | same as x, without lvalue |
| x+=y (x-=y x*=y x/=y x\=y x%=y x&=y x|=y x^=y x<<=y x>>=y) | number& | number& | number |
| x..=y | string& | string& | string |
| x,y | same as y | void | anything |
| x[y] | element type of x | array type | number |
Ternary Operations
| Operation | Operation type | x type | y type | z type |
| x?y:z | same as y | number | anything | same as y |
Function Call
When it comes to the function call, things get a little more complicated. If the function has N arguments, the function call operation has N+1 children, where the first child is the function itself, and the rest of the children correspond to the function arguments.
However, we will not allow implicitly passing arguments by reference. We will require the caller to prefix them with the & sign. For now, that will not be an additional operator but the way the function call is parsed. If we don’t parse the ampersand, when the argument is expected, we will remove the lvalue-ness from that argument by adding a fake unary operation that we call node_operation::param. That operation has the same type as its child, but it is not an lvalue.
Then, when we build the node with that call operation, if we have an argument that is lvalue but is not expected by the function, we will generate an error, as it means that the caller typed the ampersand accidentally. Somewhat surprisingly, that &, if treated as an operator, would have the least precedence, as it doesn’t have the meaning semantically if parsed inside the expression. We may change it later.
Expression Parser
In one of his claims about the potential of programmers, famous computer science philosopher Edsger Dijkstra once said:
“It is practically impossible to teach good programming to students that have had a prior exposure to BASIC. As potential programmers, they are mentally mutilated beyond hope of regeneration.”
So, for all of you that haven’t been exposed to BASIC - be grateful, as you escaped “mental mutilation.”
The rest of us, mutilated programmers, let us remind ourselves of the days when we coded in BASIC. There was an operator \, which was used for integral division. In a language where you don’t have separate types for integral and floating point numbers, that’s quite handy, so I added the same operator to Stork. I also added the operator \=, which will, as you guessed, perform integral division and then assign.
I think such operators would be appreciated by JavaScript programmers, for example. I don’t want to even imagine what Dijkstra would say about them if he lived long enough to see the rising popularity of JS.
Speaking of which, one of the biggest issues that I have with JavaScript is the discrepancy of the following expressions:
-
"1" - “1”evaluates to0 -
"1" * “1”evaluates to1 -
"1" / “1”evaluates to1 -
"1" + “1”evaluates to“11”
Croatian hip-hop duo “Tram 11,” named after a tram that connects Zagreb’s outlying boroughs, had a song which roughly translates as: “One and one are not two, but 11.” It came out in the late 90s, so it wasn’t a reference to JavaScript, but it illustrates the discrepancy quite well.
To avoid those discrepancies, I prohibited implicit conversion from string to number, and I added .. operator for the concatenation (and ..= for the concatenation with assignment). I don’t remember where I got the idea for that operator. It is not from BASIC or PHP, and I will not search the phrase “Python concatenation” because googling anything about Python sends chills down my spine. I have a phobia of snakes, and combining that with “concatenation” - no, thanks! Maybe later, with some archaic text-based browser, without ASCII art.
But back to the topic of this section - our expression parser. We will use an adaptation of “Shunting-yard Algorithm.”
That is the algorithm that comes to the mind of any even average programmer after thinking about the problem for 10 minutes or so. It can be used to evaluate an infix expression or transform it to the reverse Polish notation, which we will not do.
The idea of the algorithm is to read operands and operators from left to right. When we read an operand, we push it to the operand stack. When we read an operator, we cannot evaluate it immediately, as we don’t know if the following operator will have better precedence than that one. Therefore, we push it to the operator stack.
However, we first check if the operator at the top of the stack has better precedence than the one that we just read. In that case, we evaluate the operator from the top of the stack with operands on the operand stack. We push the result to the operand stack. We keep it until we read everything and then evaluate all the operators on the left of the operator stack with the operands on the operand stack, pushing results back on the operand stack until we are left with no operators and with just one operand, which is the result.
When two operators have the same precedence, we will take the left one in case those operators are left-associative; otherwise, we take the right one. Two operators of the same precedence cannot have different associativity.
The original algorithm also treats round brackets, but we will do it recursively instead, since the algorithm will be cleaner that way.
Edsger Dijkstra named the algorithm “Shunting-yard” because it resembles the operation of a railroad shunting yard.
However, the original shunting-yard algorithm does almost no error checking, so it is quite possible that an invalid expression is parsed as a correct one. Therefore, I added the boolean variable which checks if we expect an operator or an operand. If we expect operands, we can parse unary prefix operators, as well. That way, no invalid expression can pass under the radar, and expression syntax check is complete.
Wrapping Up
When I started coding for this part of the series, I planned to write about the expression builder. I wanted to build an expression that can be evaluated. However, it turned out to be way too complicated for one blog post, so I decided to split it in half. In this part, we concluded parsing expressions, and I will write about building expression objects in the next article.
If I recall correctly, some 15 years ago, it took me one weekend to write the first version of my first language, which makes me wonder what went wrong this time.
In an effort to deny I’m getting older and less witty, I will blame my two-year-old son for being too demanding in my spare time.
As in Part 1, you are welcome to read, download, or even compile the code from my GitHub page.
Understanding the basics
What is expression parsing?
The process that translates a sequence of operations and operands into a structure that can be easily computed, such as an expression tree.
What is the difference between statically typed and dynamically typed languages?
If types of variables are checked during the compilation, the language is statically typed. Otherwise, it is dynamically typed.
What is a regular expression used for?
It is used for pattern matching - recognizing a part of a text that satisfies a certain pattern.
Jakiša Tomić
Zagreb, Croatia
Member since November 13, 2019
About the author
Jakisa has 15+ years of experience developing various apps on multiple platforms. Most of his technical expertise is in C++ development.
Expertise
PREVIOUSLY AT


