Interview: The Promise of Intel oneAPI and Direct Parallel C++

Intel is not the first name that comes to mind when you think about software development, even though it’s one of the most influential and innovative technology companies on the planet. Four decades ago, Intel’s 8088 processor helped launch the PC revolution, and if you’re reading this on a desktop or a laptop, chances are you have an Intel Inside. The same goes for servers and a range of other hardware we rely on every day. That’s not to say AMD and other vendors don’t have competitive products because they do, but Intel still dominates the x86 CPU market.

Software engineers have been using Intel hardware platforms for decades, typically without even considering the software and firmware behind them. If they needed more virtualization performance, they opted for multicore, hyperthreaded Core i7, or Xeon products. For local database tinkering, they could get an Intel SSD. But now, Intel wants developers to start using more of its software, too.

What Is Intel oneAPI?

Enter oneAPI, touted by Intel as a single, unified programming model that aims to simplify development across different hardware architectures: CPUs, GPUs, FPGAs, AI accelerators, and more. All of them have very different properties and excel at different types of operations.

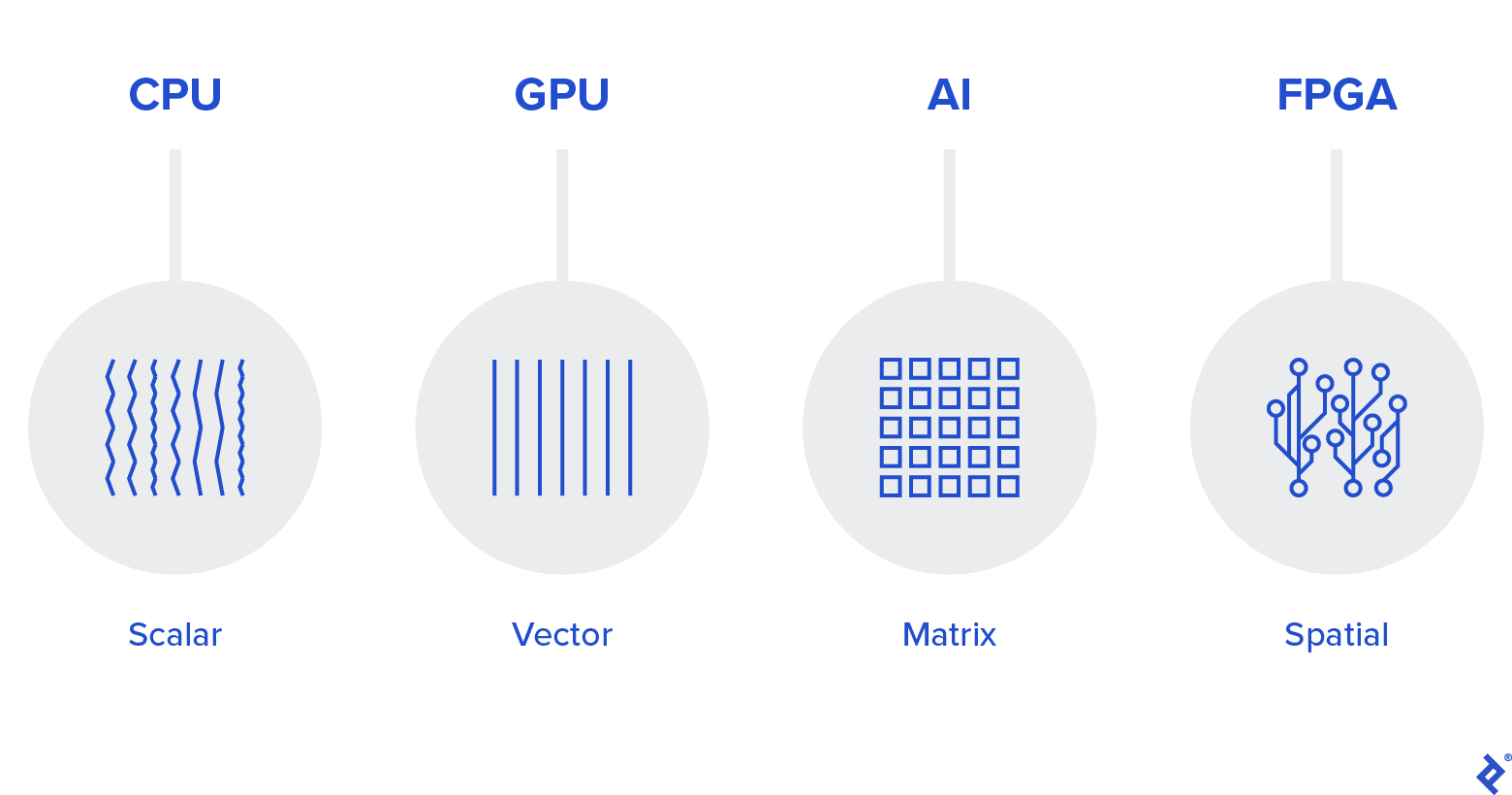
Intel is now committed to a “software-first” strategy and expects developers to take notice. The grand idea behind oneAPI is to enable the use of one platform for a range of different hardware, hence developers would not have to use different languages, tools, and libraries when they code for CPUs and GPUs, for example. With oneAPI, the toolbox and codebase would be the same for both.

To make this possible, Intel developed Data Parallel C++ (DPC++) as an open-source alternative to proprietary languages typically used to program for specific hardware (e.g., GPUs or FFPGAs). This new programming language is supposed to deliver the productivity and familiarity of C++ while including a compiler to deploy across different hardware targets.

Data Parallel C++ also incorporates Khronos Group’s SYCL to support data parallelism and heterogeneous programming. Intel is currently offering free access to its DevCloud, allowing software engineers to try out their tools and tinker with oneAPI and DPC++ in the cloud without much hassle.

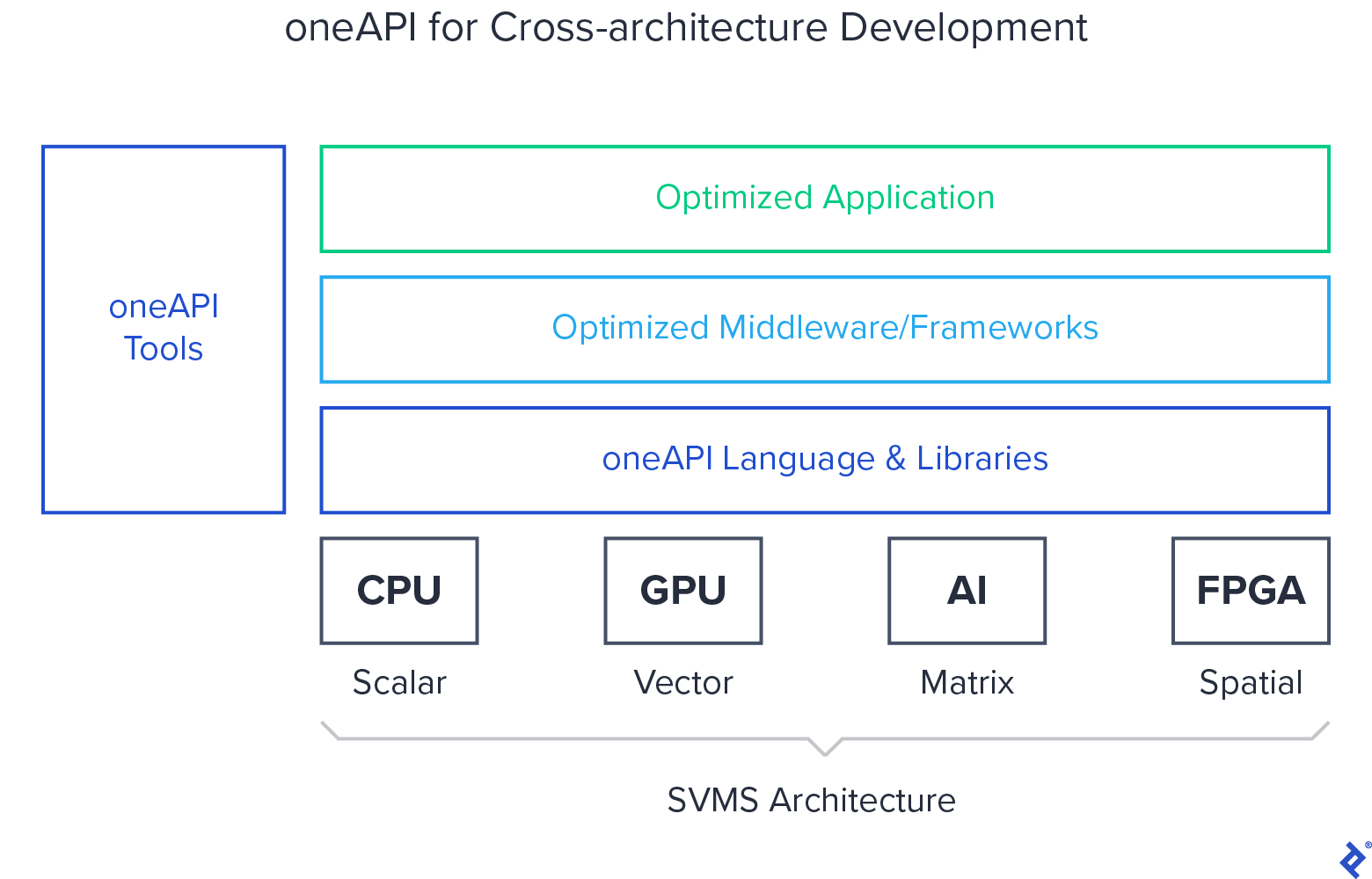
But wait, will it work on hardware made by other vendors? What about licensing, is it free? Yes and yes: oneAPI is designed to be hardware-agnostic and open-source, and that won’t change.

To learn more about oneAPI, we discussed its genesis and future with Sanjiv M. Shah, the Vice President of Intel’s Architecture, Graphics and Software Group and general manager of Technical, Enterprise, and Cloud Computing at Intel.

Sanjiv: In terms of what is in oneAPI, I think about it as four pieces. One is a language and a standard library, the second is a set of deep learning tools, the third is really a hardware abstraction layer and a software driver layer that can abstract different accelerators, and the fourth piece is a set of domain-focused libraries, like Matlab and so on. Those are the four categories of things in oneAPI, but we can go deeper and talk about the nine elements of oneAPI. Those nine elements are basically the new language we’re introducing called Data Parallel C++ and its standard library.

There are two learning libraries, one for neural networks and one for communications. There’s the library we’re calling level zero that’s for hardware abstraction, and there are four domain-focused libraries. We are doing this in a very, very open way. The specs for all of these are already open and available. We’re calling them version 0.5. We intend to drive to 1.0 by the end of 2020, and we also have open-source implementations of all of these. Again, our goal is to enable people to leverage what is out there already. If a hardware vendor wants to implement this language, they can take what’s open-sourced and run with it.

Q: Regarding algorithms and implementation, how does that work?

What we’re providing is the primitives that the algorithms would use: the underlying mathematical primitives and communication primitives. Typically, algorithm innovation is happening at a higher level than that, where they’re not really redoing the fundamental math, matrix math, convolution math, and so on. It is about figuring new ways to use that math and new ways to use communication patterns. Our goal really is for us to provide the primitive, the level zero, so that others may innovate on top of it.

Q: How does it work on a hardware level?

If you are a hardware provider, let’s take an AI matrix, someone building an AI ASIC, for example—there’s two ways for that hardware vendor to “plug in” and leverage the AI ecosystem. One would be to provide this low-level hardware interface we’re calling level zero, and if they provide their version of level zero using the standard API, they can leverage the open source if they want to, and then all the software layers above can automatically leverage that.

That might be hard for a segment-focused ASICs, to provide the full generality of level zero. So, as an alternative to that, they can also just provide the math kernels and communication kernels that are in our domain and deep learning libraries, and then we will do the job of “plumbing” those libraries into the higher-level frameworks, so they would get that automatically.

Q: You mentioned that the version you have right now is designated 0.5, and the full spec should be ready by the end of 2020.

So, there are two parts to our oneAPI initiative. One is the industry part, and one is Intel products. The industry spec is at 0.5, and around mid-year, we’d like to get that to 1.0. In parallel with that, Intel is building a set of products, and the products Intel is building are today in beta and they implement the 0.5 spec. By the end of the year, we would like to get to a 1.0 product.

Intel’s product goes beyond the nine elements of oneAPI because, in addition to the basic programming elements we provide, we also want to provide the things that programmers really need, like debuggers, analyzers, and compatibility tools so they migrate from existing languages into the Data Parallel C++ language.

Q: How hard is it for the developer to transition? Is the broader environment similar to what they’ve been using for years?

Yes, it is very similar. Let me describe Data Parallel C++ a little bit because that is a big part of what we are doing. DPC++ is three things. It builds on the ISO international standard C++ language. There’s a group called Khronos that defines the standard called SYCL, and SYCL is layered on top of C++. We take SYCL, and then we add extensions on top of SYCL. The way we are building Data Parallel C++, it really is just C++ with extensions on it, which is what SYCL is.

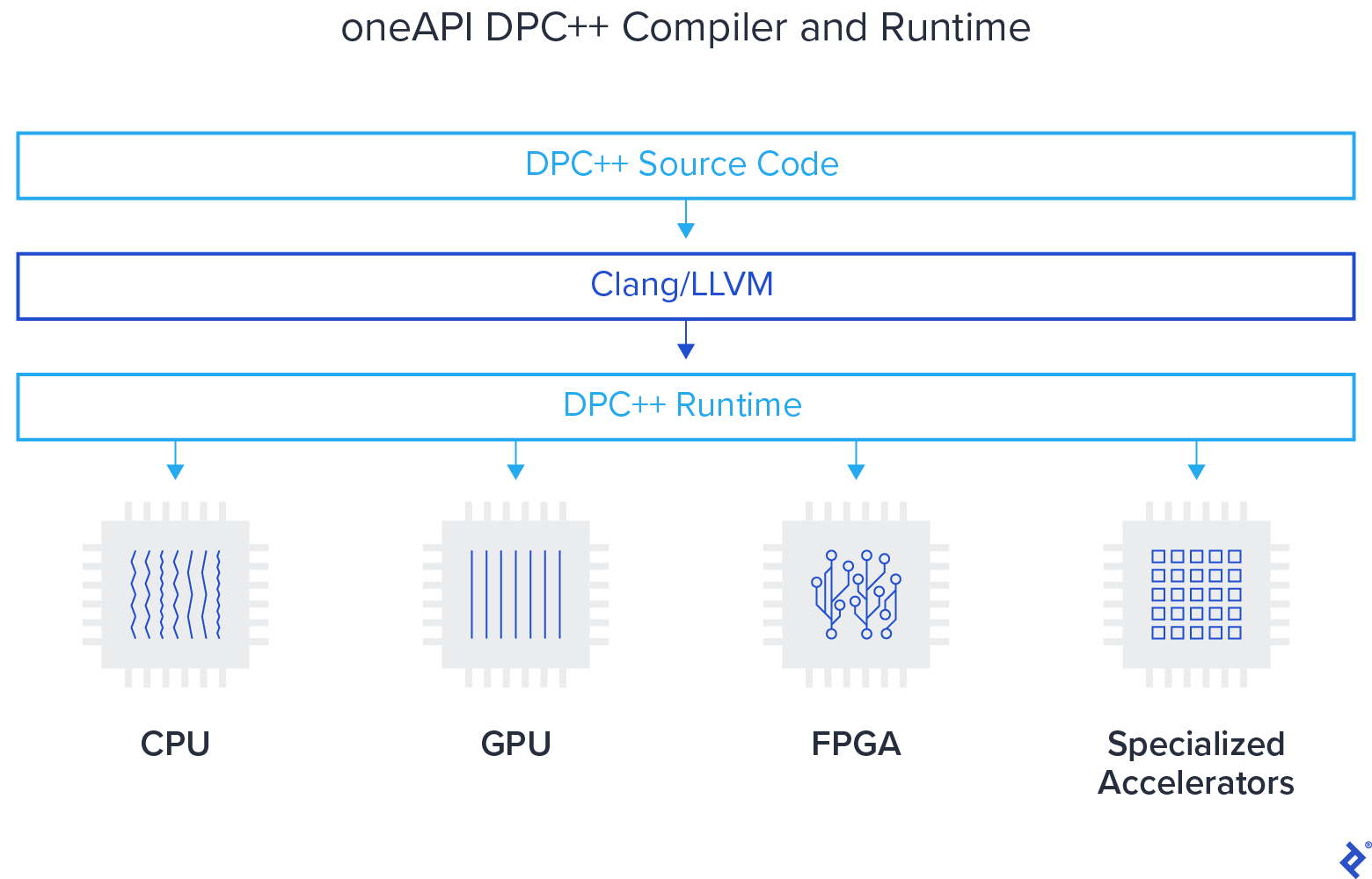
Any C++ compiler can compile it. The beauty of DPC++ is that any compiler can compile it, just a knowledgeable compiler can take advantage of what’s in that language and generate accelerator code. The way we’re conducting this language, we’re doing it very, very openly, so all our discussions about Data Parallel C++ are happening with the SYCL committee. The implementations are open-source, all the extensions are published already, and we’re working very, very carefully to make sure that we have a nice glidepath into the future SYCL standards. Looking down at 5-10 years from now, a glidepath into ISO C++ also.

Q: Regarding the compilers and migrating to DPC++, the learning curve shouldn’t be much of a problem?

Yes, it depends where you are starting from, of course. For a C++ programmer, the learning curve would be very small. For a C programmer, you would have to get over the hurdle of learning C++, but that’s all. It’s very familiar C++. For a programmer used to languages like OpenCL, it should be very similar.

The other part I must stress is that we’re doing the work in open source using the LLVM infrastructure. All our source is already open, there’s an Intel GitHub repository where you can go and look at the language implementation, even download an open-source compiler. All of Intel tools, our product offerings that are beta are also available for free for anyone to play with and download. We also have a developer cloud available, where people don’t need to download or install anything, they can just write the code and start using all the tools we talked about.

Q: C++ is performant and relatively simple, but we all know it’s getting old, development is slow, there are too many stakeholders, so they’re slowing everything down. This obviously wouldn’t be the case with DPC++. You would have much faster iterations and updates?

I think you’ve hit a very, very important point for us, which is fast evolution that’s not slowed down by standards. So, we want to do our discussions openly with the standard, so there’s a way to get into the standards, but we also want to do it quickly.

Languages work best when they’re co-designed by their users and implementers, as architectures evolve. Our goal is really fast iterative code design where we’re practicing things, finding the best way to do things, and making them standard. So, absolutely, fast iteration is a big goal.

Q: One question that was raised by some of my colleagues (you can probably understand that they are somewhat concerned about the openness with anything coming from a big corporation): Will DPC++ always remain open to all users and vendors?

Absolutely! The spec is done with a creative commons license. Anybody can use the spec, take it and fork it if they want, and evolve it. I want to stress that not all elements of oneAPI are open-sourced, but we are on a path to make almost all elements open-source. All of that, anybody can grab and leverage - it’s available for implementation.

Codeplay, which is a company out of the UK, announced an Nvidia implementation of DPC++, and we’re really encouraging all hardware vendors and software vendors to do their port. We’re at a unique point in the industry where accelerators are becoming common for multiple vendors. When that happens in history, when there’s only one provider, their language dominates. The software industry demands a standard solution and multiple providers.

What we’re trying to do here is what we did about two and a half decades ago with OpenMP, where there were multiple parallel languages but no single really dominant one. We took all of that and unified it into a standard that now, 25 years later, is the way to program for HPC.

Q: Would it be correct to say that DPC++ is going to see a lot of evolution over the next few years? What about tensors, what about new hardware coming out?

Yes, absolutely, you are right. We have to evolve the language to support the new hardware that’s coming out. That is the goal of faster iteration. Another point I want to stress is that we are designing Data Parallel C++ so that you can also plug in architecture-specific extensions if you want to.

So, while it is a standard language that we want to run across multiple architectures, we also realize that sometimes, an audience, a very important audience needs the maximum performance possible. They may want to dive down to very low-level programming that will not necessarily be architecture-portable. We’re building extensions and mechanisms so you can have extensions for tensors and so on that would be architecture-specific.

Q: How much control over the code generated for the hardware could a developer have? How much control can they have over memory management between the system and various accelerators?

We’re borrowing the concept of buffers from SYCL, which give very explicit memory control to the user, but in addition to that, we’re also adding the notion of unified memory. Our goal is to allow the programmer a level of control that they need, not just to manage memory but to generate quick code. Some of the extensions that we’re adding over SYCL are things like subgroups, reductions, pipes, and so on. That will let you generate much better code for different architectures.

Q: An interesting point is the oneAPI distribution for Python—Intel specifically listed NumPy, SciPy, SciKit Learn. I am curious about the performance gain and the productivity benefits that could be unlocked through oneAPI. Do you have any metrics on that?

That’s an excellent question. We’re supporting that ecosystem. Why would Python want to use an accelerator? It’s to get performance out of its math libraries, analytics libraries. What we’re doing is “plumbing” NumPy, SciPy, SciKit Learn, etc., so that we can get good performance leveraging the libraries that we have on top of it. The default implementation of NumPy, SciPy, SciKit Learn, and so on, compared to the one that’s plumbed properly with optimized native packages, can see very, very large gains. We’ve seen gains on the order of 200x, 300x, etc.

Our goal with Python is that we would want to get within a reasonable fraction, within 2x, maybe within 80 percent of native code performance. The state of the art today is that you’re frequently at 10x or more. We want to really bridge that gap by plumbing all the high-performance tasks so that you’re within a factor of 2, and actually much higher than that.

Q: What types of hardware are we talking about? Could developers unlock this potential on an ordinary workstation, or would it necessitate something a bit more powerful?

No, it would be everywhere. If you think about where the gain is coming from, then you will understand. The normal Python libraries are not using any of the virtualization capabilities on CPUs. They’re not using any of the multi-core capabilities on CPUs. They are not optimized, the memory system and all that is not optimized. So, it comes down to a matrix multiply that’s written by a naive programmer and compiled by a compiler without any optimization, and then compare that to what an expert writes in assembly code. You can see multi-100x gains when you compare those two, and in the Python world, essentially, that’s what’s happening.

The Python interpreters and standard libraries are so high-level that the code you end up with becomes very, very naive code. When you plumb it properly with optimized libraries, you get those huge gains. A laptop already has two to six or eight CPU cores, they’re multithreaded and have pretty decent vectorization capabilities in them, maybe it’s 256, maybe it’s 512. So, there is a lot of performance sitting in laptops and workstations. When you scale that up to GPUs, once you have graphics available, you can imagine where the gains are coming from.

If you look at our integrated graphics, they’re also getting very powerful. I’m sure you’ve seen the Ice Lake Gen 11, where the integrated graphics are significantly better than the previous generation. You can see where the benefits would come from, even on laptops.

Q: What about DevCloud availability? If I recall correctly, it’s free to use for everyone at the moment, but will it stay that way after you go gold next year?

That’s a good question. At this point, I’ll be honest, I don’t know the answer. Our intention at this point is for it to be free forever. It’s for development, for playing around, and there’s a lot of horsepower there, so people can actually do their runs.

Q: So, you wouldn’t mind if we asked a few thousand developers to give it a go?

Oh, absolutely not. We would love for that to happen!

I can summarize what we’re trying to do. First, we’re very, very excited about oneAPI. It’s time that a multi-vendor solution takes off, as there are multiple vendors available in the market now. If you take a look at our processor line, not just the GPUs that are coming, more and more powerful integrated GPUs, and our FPGA roadmap, this is an exciting time to build a standard for all of that. Our goal is productivity, performance, and industry infrastructure so that you can build upon it.

As for the three audiences I talked about, application developers can leverage things easily, as they are already available. Hardware vendors can take advantage of the software stack and plug in new hardware, while tool and language vendors can easily use it. Intel cannot build all the languages and all the tools in the world, so it’s an open-source infrastructure that others can leverage and build upon very easily.