Identifying the Unknown With Clustering Metrics
Clustering in machine learning has a variety of applications, but how do you know which algorithm is best suited to your data? Here’s how to amplify your data insights with comparison metrics, including the F-measure.
Clustering in machine learning has a variety of applications, but how do you know which algorithm is best suited to your data? Here’s how to amplify your data insights with comparison metrics, including the F-measure.
Surbhi is a data scientist and developer with expertise in machine learning and robotics. A former senior data science engineer at Utopia Global, her experience ranges across ML fields including NLP, computer vision, and OCR. She has a master’s degree in mechatronics, and has published research in the field of robotics and optimization.
Expertise
Clustering is an unsupervised machine learning method to divide given data into groups based solely on the features of each sample. Sorting data into clusters can help identify unknown similarities between samples or reveal outliers in the data set. In the real world, clustering has significance across diverse fields from marketing to biology: Clustering applications include market segmentation, social network analysis, and diagnostic medical imaging.
Because this process is unsupervised, multiple clustering results can form around different features. For example, imagine you have a data set composed of various images of red trousers, black trousers, red shirts, and black shirts. One algorithm might find clusters based on clothing shape, while another might create groups based on color.
When analyzing a data set, we need a way to accurately measure the performance of different clustering algorithms; we may want to contrast the solutions of two algorithms, or see how close a clustering result is to an expected solution. In this article, we will explore some of the metrics that can be used for comparing different clustering results obtained from the same data.
Understanding Clustering: A Brief Example
Let’s define an example data set that we will use to explain various clustering metric concepts and examine what kinds of clusters it might produce.
First, a few common notations and terms:
- $D$: the data set
- $A$, $B$: two clusters that are subsets of our data set
- $C$: the ground truth clustering of $D$ that we will compare another cluster to
- Clustering $C$ has $K$ clusters, $C = {C_1, …, C_k}$
- $C’$: a second clustering of $D$
- Clustering $C’$ has $K’$ clusters, $C’ = {C^\prime_1, …, C^\prime_{k^\prime}}$
Clustering results can vary based not only on sorting features but also the total number of clusters. The result depends on the algorithm, its sensitivity to small perturbations, the model’s parameters, and the data’s features. Using our previously mentioned data set of black and red trousers and shirts, there are a variety of clustering results that might be produced from different algorithms.
To distinguish between general clustering $C$ and our example clusterings, we will use a lowercase $c$ to describe our example clusterings:
- $c$, with clusters based on shape: $c = {c_1, c_2}$, where $c_1$ represents trousers and $c_2$ represents shirts
- $c’$, with clusters based on color: $c’ = {c’_1, c’_2}$, where $c’_1$ represents red clothes and $c’_2$ represents black clothes
- $c’’$, with clusters based on shape and color: $c’’ = {{c^{\prime \prime}}_1, {c^{\prime \prime}}_2, {c^{\prime \prime}}_3, {c^{\prime \prime}}_4}$, where ${c^{\prime \prime}}_1$ represents red trousers, ${c^{\prime \prime}}_2$ represents black trousers, ${c^{\prime \prime}}_3$ represents red shirts, and ${c^{\prime \prime}}_4$ represents black shirts
Additional clusterings might include more than four clusters based on different features, such as whether a shirt is sleeveless or sleeved.
As seen in our example, a clustering method divides all the samples in a data set into non-empty disjoint subsets. In cluster $c$, there is no image that belongs to both the trouser subset and the shirt subset: $c_1 \cap c_2 = \emptyset$. This concept can be extended; no two subsets of any cluster have the same sample.
An Overview of Clustering Comparison Metrics
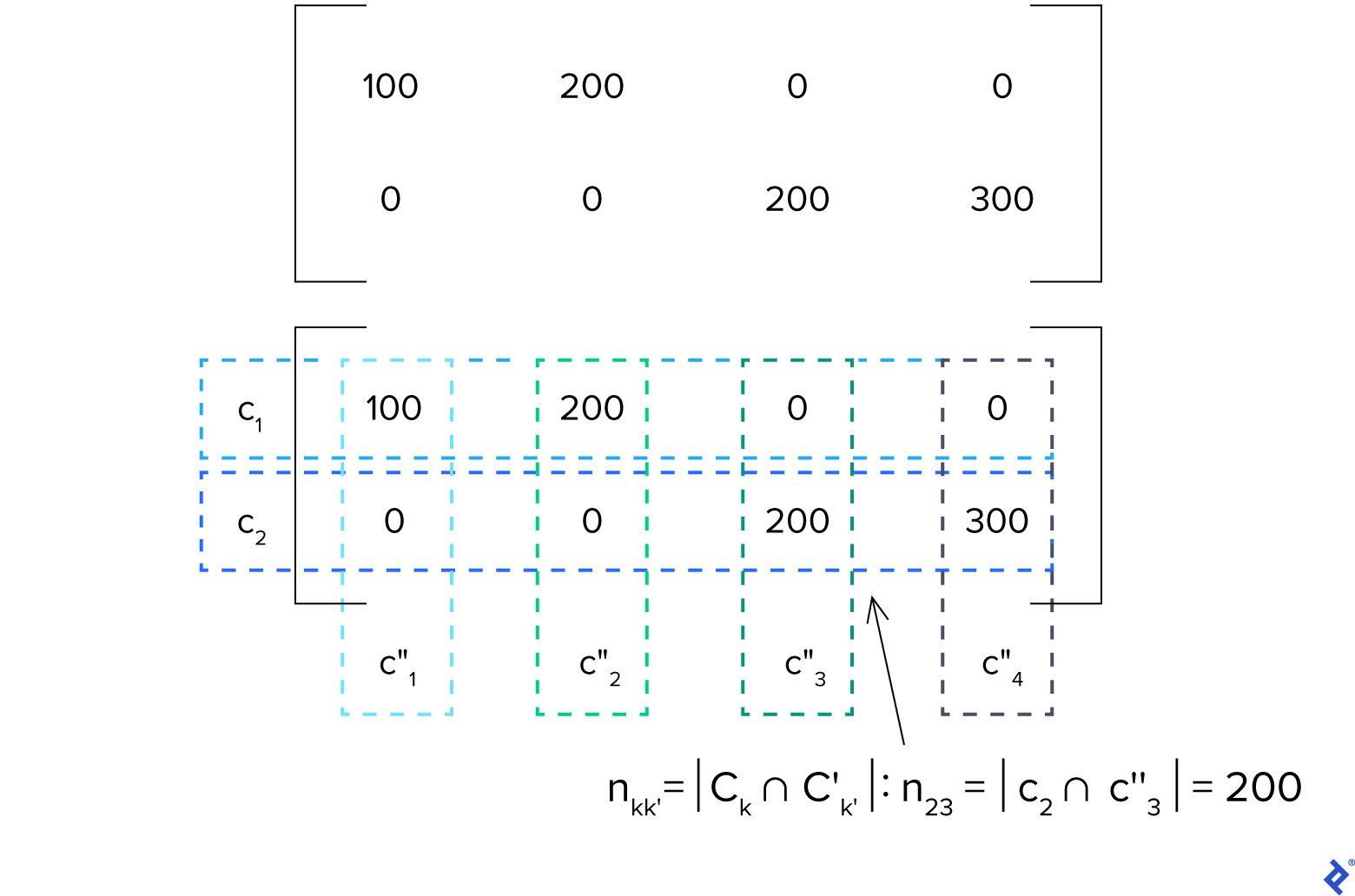
Most criteria for comparing clusterings can be described using the confusion matrix of the pair $C, C’$. The confusion matrix would be a $K \times K’$ matrix whose $kk’$th element (the element in the $k$th row and $k’$th column) is the number of samples in the intersection of clusters $C_k$ of $C$ and $C’_{k’}$ of $C’$:
\[n_{kk'} = |C_k \cap C'_{k'}|\]We’ll break this down using our simplified black and red trousers and shirts example, assuming that data set $D$ has 100 red trousers, 200 black trousers, 200 red shirts, and 300 black shirts. Let’s examine the confusion matrix of $c$ and $c’’$:
Since $K = 2$ and $K’’ = 4$, this is a $2 \times 4$ matrix. Let’s choose $k = 2$ and $k’’ = 3$. We see that element $n_{kk’} = n_{23} = 200$. This means that the intersection of $c_2$ (shirts) and ${c^{\prime\prime}}_3$ (red shirts) is 200, which is correct since $c_2 \cap {c^{\prime\prime}}_3$ would simply be the set of red shirts.
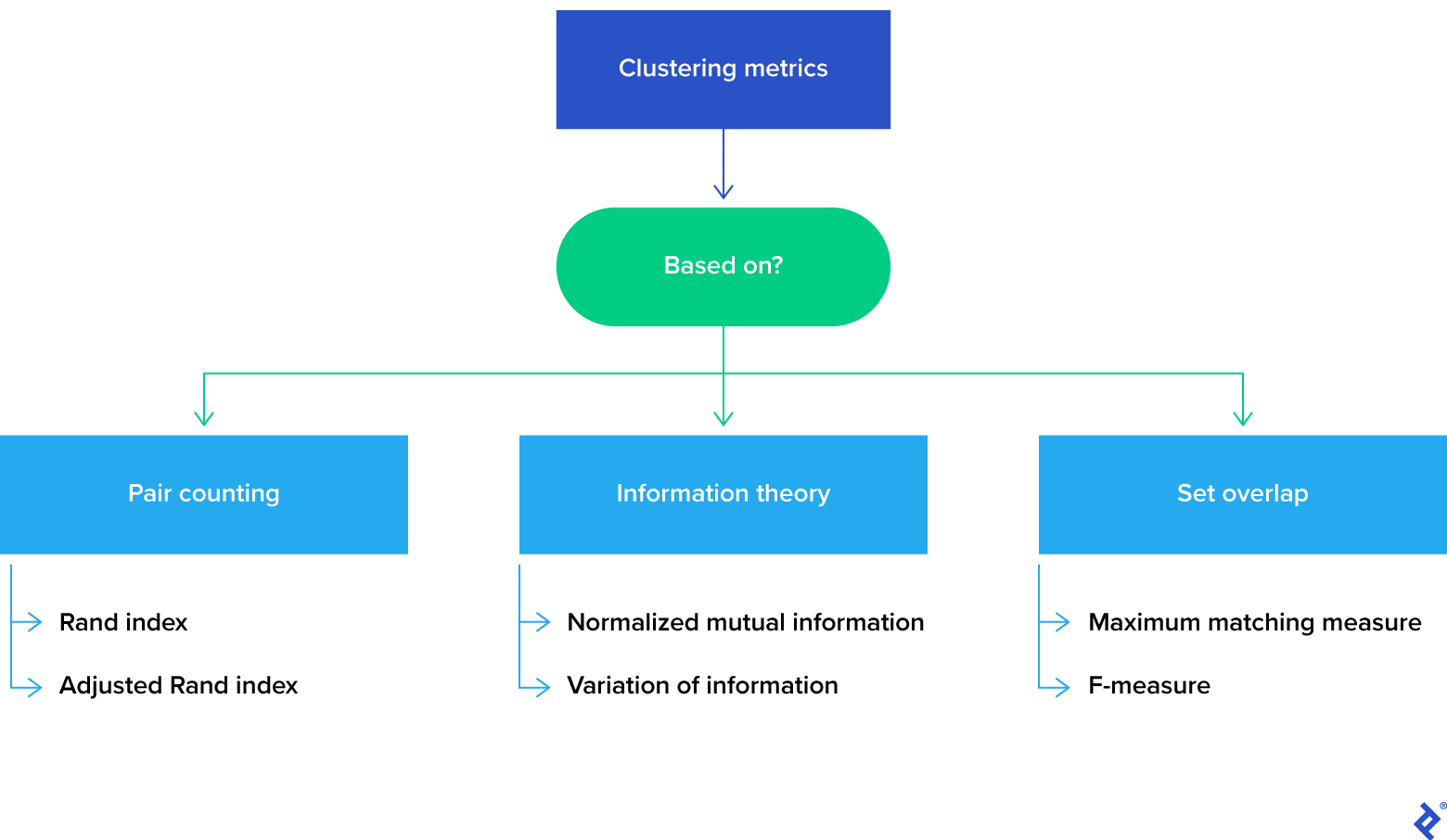
Clustering metrics can be broadly categorized into three groups based on the underlying cluster comparison method:
In this article, we only touch on a few of many metrics available, but our examples will serve to help define the three clustering metric groups.
Pair-counting
Pair-counting requires examining all pairs of samples, then counting pairs where the clusterings agree and disagree. Each pair of samples can belong to one of four sets, where the set element counts ($N_{ij}$) are obtained from the confusion matrix:
- $S_{11}$, with $N_{11}$ elements: the pair’s elements are in the same cluster under both $C$ and $C’$
- A pair of two red shirts would fall under $S_{11}$ when comparing $c$ and $c’’$
- $S_{00}$, with $N_{00}$ elements: the pair’s elements are in different clusters under both $C$ and $C’$
- A pair of a red shirt and black trousers would fall under $S_{00}$ when comparing $c$ and $c’’$
- $S_{10}$, with $N_{10}$ elements: the pair’s elements are in the same cluster in $C$ and different clusters in $C’$
- A pair of a red shirt and a black shirt would fall under $S_{10}$ when comparing $c$ and $c’’$
- $S_{01}$, with $N_{01}$ elements: the pair’s elements are in different clusters in $C$ and the same cluster in $C’$
- $S_{01}$ has no elements ($N_{01} = 0$) when comparing $c$ and $c’’$
The Rand index is defined as $(N_{00} + N_{11})/(n(n-1)/2)$, where $n$ represents the number of samples; it can also be read as (number of similarly treated pairs)/(total number of pairs). Although theoretically its value ranges between 0 and 1, its range is often much narrower in practice. A higher value means more similarity between the clusterings. (A Rand index of 1 would represent a perfect match where two clusterings have identical clusters.)
One limitation of the Rand index is its behavior when the number of clusters increases to approach the number of elements; in this case, it converges toward 1, creating challenges in accurately measuring clustering similarity. Several improved or modified versions of the Rand index have been introduced to address this issue. One variation is the adjusted Rand index; however, it assumes that two clusterings are drawn randomly with a fixed number of clusters and cluster elements.
Information Theory
These metrics are based on generic notions of information theory. We will discuss two of them: entropy and mutual information (MI).
Entropy describes how much information there is in a clustering. If the entropy associated with a clustering is 0, then there is no uncertainty about the cluster of a randomly picked sample, which is true when there is only one cluster.
MI describes how much information one clustering gives about the other. MI can indicate how much knowing the cluster of a sample in $C$ reduces the uncertainty about the cluster of the sample in $C’$.
Normalized mutual information is MI that is normalized by the geometric or arithmetic mean of the entropies of clusterings. Standard MI is not bound by a constant value, so normalized mutual information provides a more interpretable clustering metric.
Another popular metric in this category is variation of information (VI) that depends on both the entropy and MI of clusterings. Let $H(C)$ be the entropy of a clustering and $I(C, C’)$ be the MI between two clusterings. VI between two clusterings can be defined as $VI(C,C’) = H(C)+H(C’)-2I(C,C’)$. A VI of 0 represents a perfect match between two clusterings.
Set Overlap
Set overlap metrics involve determining the best match for clusters in $C$ with clusters in $C’$ based on maximum overlap between the clusters. For all metrics in this category, a 1 means the clusterings are identical.
The maximum matching measure scans the confusion matrix in decreasing order and matches the largest entry of the confusion matrix first. It then removes the matched clusters and repeats the process sequentially until the clusters are exhausted.
The F-measure is another set overlap metric. Unlike the maximum matching measure, the F-measure is frequently used to compare a clustering to an optimal solution, instead of comparing two clusterings.
Applying Clustering Metrics With F-measure
Because of the F-measure’s common use in machine learning models and important applications such as search engines, we’ll explore the F-measure in more detail with an example.
F-measure Definition
Let’s assume that $C$ is our ground truth, or optimal, solution. For any $k$th cluster in $C$, where $k \in [1, K]$, we’ll calculate an individual F-measure with every cluster in clustering result $C’$. This individual F-measure indicates how well the cluster $C^\prime_{k’}$ describes the cluster $C_k$ and can be determined through the precision and recall (two model evaluation metrics) for these clusters. Let’s define $I_{kk’}$ as the intersection of elements in $C$’s $k$th cluster and $C’$’s $k’$th cluster, and $\lvert C_k \rvert$ as the number of elements in the $k$th cluster.
-
Precision $p = \frac{I_{kk’}}{\lvert C’_{k’} \rvert}$
-
Recall $r = \frac{I_{kk’}}{\lvert C_{k} \rvert}$
Then, the individual F-measure of the $k$th and $k’$th cluster can be calculated as the harmonic mean of the precision and recall for these clusters:
\[F_{kk'} = \frac{2rp}{r+p} = \frac{2I_{kk'}}{|C_k|+|C'_{k'}|}\]Now, to compare $C$ and $C’$, let’s look at the overall F-measure. First, we will create a matrix similar to a contingency table whose values are the individual F-measures of the clusters. Let’s assume that we’ve mapped $C$’s clusters as rows of a table and $C’$’s clusters as columns, with table values corresponding to individual F-measures. Identify the cluster pair with the maximum individual F-measure, and remove the row and column corresponding to these clusters. Repeat this until the clusters are exhausted. Finally, we can define the overall F-measure:
\[F(C, C') = \frac{1}{n} \sum_{i=1}^K n_imax(F(C_i, C'_j)) \forall j \in {1, K'}\]As you can see, the overall F-measure is the weighted sum of our maximum individual F-measures for the clusters.
Data Setup and Expected Results
Any Python notebook suitable for machine learning, such as a Jupyter notebook, will work as our environment. Before we start, you may want to examine my GitHub repository’s README, extended readme_help_example.ipynb example file, and requirements.txt file (the required libraries).
We’ll use the sample data in the GitHub repository, which is made up of news articles. The data is arranged with information including category, headline, date, and short_description:
| category | headline | date | short_description | |
|---|---|---|---|---|
| 49999 | THE WORLDPOST | Drug War Deaths Climb To 1,800 In Philippines | 2016-08-22 | In the last seven weeks alone. |
| 49966 | TASTE | Yes, You Can Make Real Cuban-Style Coffee At Home | 2016-08-22 | It’s all about the crema. |
| 49965 | STYLE | KFC’s Fried Chicken-Scented Sunscreen Will Kee… | 2016-08-22 | For when you want to make yourself smell finge… |
| 49964 | POLITICS | HUFFPOLLSTER: Democrats Have A Solid Chance Of… | 2016-08-22 | HuffPost’s poll-based model indicates Senate R… |
We can use pandas to read, analyze, and manipulate the data. We’ll sort the data by date and select a small sample (10,000 news headlines) for our demo since the full data set is large:
import pandas as pd
df = pd.read_json("./sample_data/example_news_data.json", lines=True)
df.sort_values(by='date', inplace=True)
df = df[:10000]
len(df['category'].unique())
Upon running, you should see the notebook output the result 30, since there are 30 categories in this data sample. You may also run df.head(4) to see how the data is stored. (It should match the table displayed in this section.)
Optimizing Clustering Features
Before applying the clustering, we should first preprocess the text to reduce redundant features of our model, including:
- Updating the text to have a uniform case.
- Removing numeric or special characters.
- Performing lemmatization.
- Removing stop words.
import re
import nltk
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
wordnet_lemmatizer = WordNetLemmatizer()
nltk.download('stopwords')
stop_words = stopwords.words('english')
nltk.download('wordnet')
nltk.download('omw-1.4')
def preprocess(text: str) -> str:
text = text.lower()
text = re.sub('[^a-z]',' ',text)
text = re.sub('\s+', ' ', text)
text = text.split(" ")
words = [wordnet_lemmatizer.lemmatize(word, 'v') for word in text if word not in stop_words]
return " ".join(words)
df['processed_input'] = df['headline'].apply(preprocess)
The resulting preprocessed headlines are shown as processed_input, which you can observe by again running df.head(4):
| category | headline | date | short_description | processed_input | |
|---|---|---|---|---|---|
| 49999 | THE WORLDPOST | Drug War Deaths Climb To 1,800 In Philippines | 2016-08-22 | In the last seven weeks alone. | drug war deaths climb philippines |
| 49966 | TASTE | Yes, You Can Make Real Cuban-Style Coffee At Home | 2016-08-22 | It’s all about the crema. | yes make real cuban style coffee home |
| 49965 | STYLE | KFC’s Fried Chicken-Scented Sunscreen Will Kee… | 2016-08-22 | For when you want to make yourself smell finge… | kfc fry chicken scent sunscreen keep skin get … |
| 49964 | POLITICS | HUFFPOLLSTER: Democrats Have A Solid Chance Of… | 2016-08-22 | HuffPost’s poll-based model indicates Senate R… | huffpollster democrats solid chance retake senate |
Now, we need to represent each headline as a numeric vector to be able to apply any machine learning model to it. There are various feature extraction techniques to achieve this; we will be using TF-IDF (term frequency-inverse document frequency). This technique reduces the effect of words occurring with high frequency in documents (in our example, news headlines), as these clearly should not be the deciding features in clustering or classifying them.
from sklearn.cluster import AgglomerativeClustering, KMeans
from sklearn.feature_extraction.text import TfidfVectorizer
vectorizer = TfidfVectorizer(max_features=300, tokenizer=lambda x: x.split(' '))
tfidf_mat = vectorizer.fit_transform(df['processed_input'])
X = tfidf_mat.todense()
X[X==0]=0.00001
Next, we will try out our first clustering method, agglomerative clustering, on these feature vectors.
Clustering Method 1: Agglomerative Clustering
Considering the given news categories as the optimal solution, let’s compare these results to those of agglomerative clustering (with the desired number of clusters as 30 since there are 30 categories in the data set):
clusters_agg = AgglomerativeClustering(n_clusters=30).fit_predict(X)
df['class_prd'] = clusters_agg.astype(int)
We will identify the resulting clusters by integer labels; headlines belonging to the same cluster are assigned the same integer label. The cluster_measure function from the compare_clusters module of our GitHub repository returns the aggregate F-measure and number of perfectly matching clusters so we can see how accurate our clustering result was:
from clustering.compare_clusters import cluster_measure
# ‘cluster_measure` requires given text categories to be in the column ‘text_category`
df['text_category'] = df['category']
res_df, fmeasure_aggregate, true_matches = cluster_measure(df, gt_column='class_gt')
fmeasure_aggregate, len(true_matches)
# Outputs: (0.19858339749319176, 0)
On comparing these cluster results with the optimal solution, we get a low F-measure of 0.198 and 0 clusters matching with actual class groups, depicting that the agglomerative clusters do not align with the headline categories we chose. Let’s check out a cluster in the result to see what it looks like.
df[df['class_prd'] == 0]['category'].value_counts()
Upon examining the results, we see that this cluster contains headlines from all the categories:
POLITICS 1268
ENTERTAINMENT 712
THE WORLDPOST 373
HEALTHY LIVING 272
QUEER VOICES 251
PARENTS 212
BLACK VOICES 211
...
FIFTY 24
EDUCATION 23
COLLEGE 14
ARTS 13
So, our low F-measure makes sense considering that our result’s clusters do not align with the optimal solution. However, it is important to recall that the given category classification we chose reflects only one possible division of the data set. A low F-measure here doesn’t imply that the clustering result is wrong, but that the clustering result didn’t match our desired method of partitioning the data.
Clustering Method 2: K-means
Let’s try another popular clustering algorithm on the same data set: k-means clustering. We will create a new dataframe and use the cluster_measure function again:
kmeans = KMeans(n_clusters=30, random_state=0).fit(X)
df2 = df.copy()
df2['class_prd'] = kmeans.predict(X).astype(int)
res_df, fmeasure_aggregate, true_matches = cluster_measure(df2)
fmeasure_aggregate, len(true_matches)
# Outputs: (0.18332960871141976, 0)
Like the agglomerative clustering result, our k-means clustering result has formed clusters that are dissimilar to our given categories: It has an F-measure of 0.18 when compared to the optimal solution. Since the two clustering results have similar F-measures, it would be interesting to compare them to each other. We already have the clusterings, so we just need to calculate the F-measure. First, we’ll bring both results into one column, with class_gt having the agglomerative clustering output, and class_prd having the k-means clustering output:
df1 = df2.copy()
df1['class_gt'] = df['class_prd']
res_df, fmeasure_aggregate, true_matches = cluster_measure(df1, gt_column='class_gt')
fmeasure_aggregate, len(true_matches)
# Outputs: (0.4030316435020922, 0)
With a higher F-measure of 0.4, we can observe that the clusterings of the two algorithms are more similar to each other than they are to the optimal solution.
Discover More About Enhanced Clustering Results
An understanding of the available clustering comparison metrics will expand your machine learning model analysis. We have seen the F-measure clustering metric in action, and gave you the basics you need to apply these learnings to your next clustering result. To learn even more, here are my top picks for further reading:
- Comparing Clusterings - An Overview by Dorothea Wagner and Silke Wagner
- Comparing clusterings—an information based distance by Marina Meilă
- Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance by Nguyen Xuan Vinh, Julien Epps, and James Bailey
The Toptal Engineering Blog extends its gratitude to Luis Bronchal for reviewing the code samples presented in this article.
Further Reading on the Toptal Blog:
Understanding the basics
What is clustering in machine learning?
Clustering is a machine learning method that divides data into groups based on the features of each sample. For example, a clustering algorithm might sort images of red and black shirts and trousers into groups based on shape (trousers and shirts), color (red items and black items), or both.
Why is clustering important in machine learning?
Clustering can identify unknown similarities between samples or reveal outliers in a data set. It has a variety of real-world applications, such as social network analysis or diagnostic medical imaging.
Which algorithm is used for clustering?
There are many algorithms that can be used for clustering. For example, k-means clustering and agglomerative clustering are two popular algorithms.
Is clustering supervised or unsupervised?
Clustering is an unsupervised machine learning method since it groups and analyzes unlabeled data sets.
What is F-measure in machine learning?
The F-measure is a statistical analysis method used to measure the correctness of a model’s output. We focus on its use as a clustering metric that can compare a clustering to an optimal solution.
What metric is used for clustering?
There are a large variety of metrics used to compare clusterings. They generally fall into one of three categories: pair-counting metrics, information theory metrics, or set overlap metrics. The Rand index and the F-measure are two of the many metrics available.
Jalpaiguri, West Bengal, India
Member since November 2, 2021
About the author
Surbhi is a data scientist and developer with expertise in machine learning and robotics. A former senior data science engineer at Utopia Global, her experience ranges across ML fields including NLP, computer vision, and OCR. She has a master’s degree in mechatronics, and has published research in the field of robotics and optimization.