A Deeper Meaning: Topic Modeling in Python
Colloquial language doesn’t lend itself to computation. That’s where natural language processing steps in. Learn how topic modeling helps computers understand human speech.
Colloquial language doesn’t lend itself to computation. That’s where natural language processing steps in. Learn how topic modeling helps computers understand human speech.
Federico is a developer and data scientist who has worked at Facebook, where he made machine learning model predictions. He is a Python expert and a university lecturer. His PhD research pertains to graph machine learning.
Expertise
PREVIOUSLY AT

Computers and the processors that power them are built to work with numbers. In contrast, the everyday language of emails and social media posts has a loose structure that doesn’t lend itself to computation.
That’s where natural language processing (NLP) comes in. NLP is a branch of computer science that overlaps with linguistics by applying computational techniques (namely artificial intelligence) to analyze natural language and speech. Topic modeling focuses on understanding which topics a given text is about. Topic modeling lets developers implement helpful features like detecting breaking news on social media, recommending personalized messages, detecting fake users, and characterizing information flow.
How can developers coax calculation-focused computers to understand human communications at those levels of sophistication?
A Bag of Words
To answer that question, we need to be able to describe a text mathematically. We’ll start our topic-modeling Python tutorial with the simplest method: bag of words.
This method represents a text as a set of words. For example, the sentence This is an example can be described as a set of words using the frequency with which those words appear:
{"an": 1, "example": 1, "is": 1, "this": 1}
Note how this method ignores word order. Take these examples:
- “I like Star Wars but I don’t like Harry Potter.”
- “I like Harry Potter but I don’t like Star Wars.”
These sentiments are represented by the same words, but they have opposite meanings. For the purposes of analyzing the topics of the texts, however, these differences do not matter. In both cases, we are talking about tastes for Harry Potter and Star Wars, regardless of what those tastes are. As such, word order is immaterial.
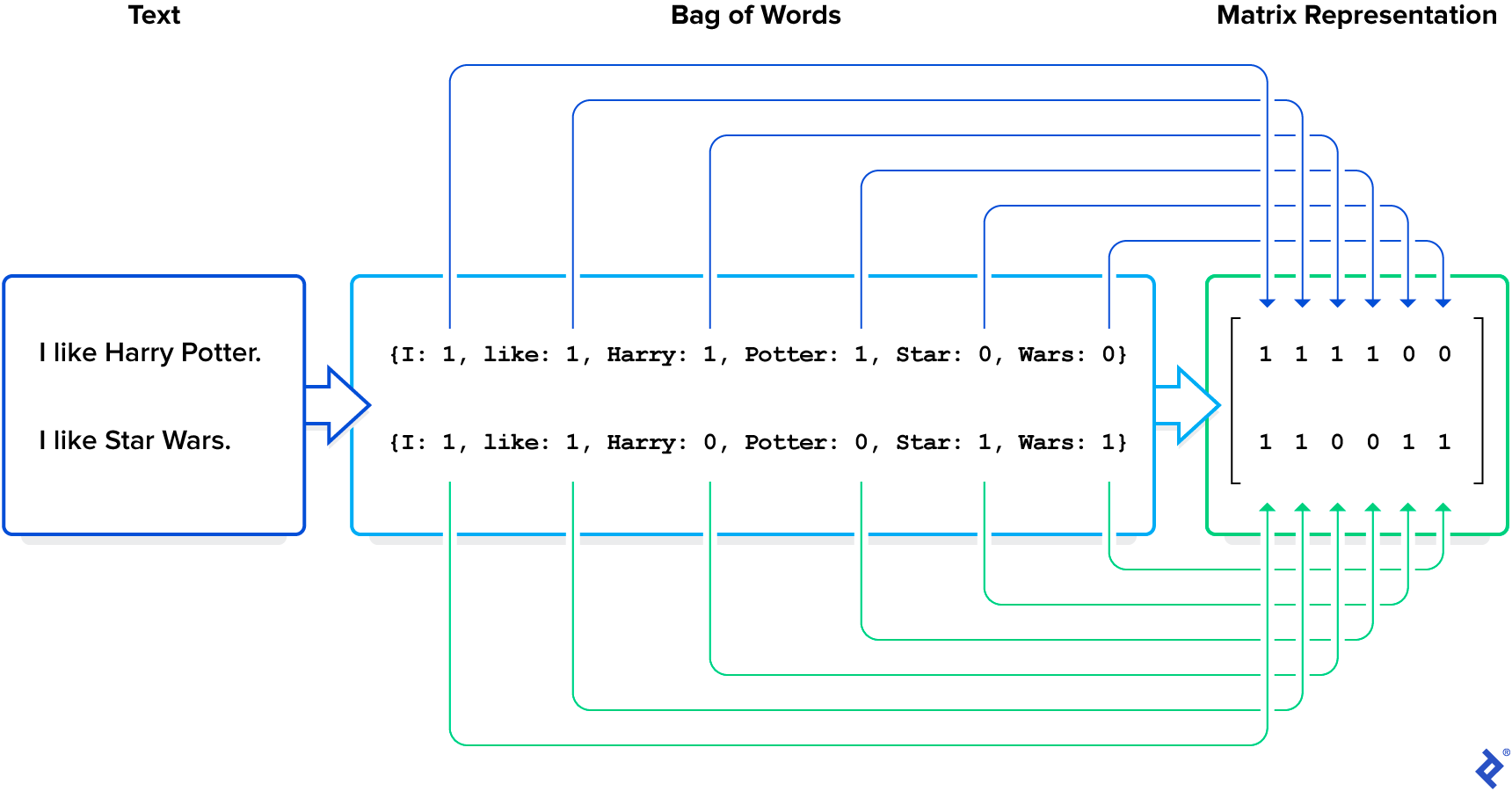
When we have multiple texts and seek to understand the differences among them, we need a mathematical representation for our entire corpus that considers each text separately. For this we can use a matrix, in which each column represents a word or term and each row represents a text. A possible representation of a corpus consists of noting in each cell the frequency with which a given word (column) is used in a certain text (row).
In our example, the corpus is composed of two sentences (our matrix rows):
["I like Harry Potter",
"I like Star Wars"]
We list the words in this corpus in the order in which we encounter them: I, like, Harry, Potter, Star, Wars. These correspond to our matrix columns.
The values in the matrix represent the number of times a given word is used in each phrase:
[[1,1,1,1,0,0],
[1,1,0,0,1,1]]
Note that the size of the matrix is determined by multiplying the number of texts by the number of different words that appear in at least one text. The latter is usually unnecessarily large and can be reduced. For example, a matrix might contain two columns for conjugated verbs, such as “play” and “played,” regardless of the fact that their meaning is similar.
But columns that describe new concepts could be missing. For example, “classical” and “music” each have individual meanings but when combined—“classical music”—they have another meaning.
Due to these issues, it is necessary to preprocess text in order to obtain good results.
Preprocessing and Topic Clustering Models
For best results, it’s necessary to use multiple preprocessing techniques. Here are some of the most frequently used:
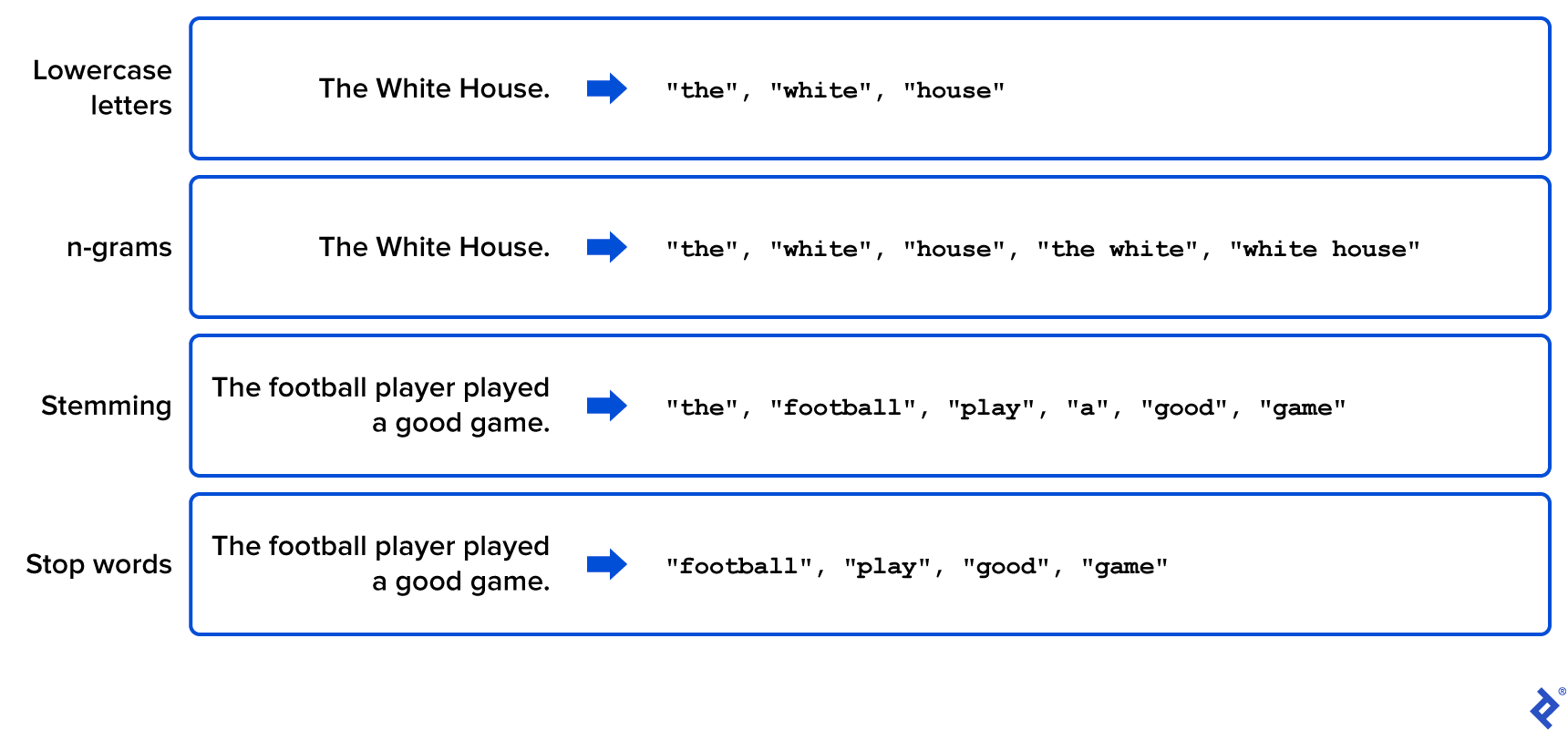
- Lowercase letters. Make all words lowercase. Make all words lowercase. The meaning of a word does not change regardless of its position in the sentence.
- n-grams. Consider all groups of n words in a row as new terms, called n-grams. This way, cases such as “white house” will be taken into account and added to the vocabulary list.
- Stemming. Identify prefixes and suffixes of words to isolate them from their root. This way, words like “play,” “played,” or “player” are represented by the word “play.” Stemming can be useful to reduce the number of words in the vocabulary list while preserving their meaning , but it slows preprocessing considerably because it must be applied to each word in the corpus.
- Stop words. Do not take into account groups of words lacking in meaning or utility. These include articles and prepositions but may also include words that are not useful for our specific case study, such as certain common verbs.
-
Term frequency–inverse document frequency (tf–idf). Use the coefficient of tf–idf instead of noting the frequency of each word within each cell of the matrix. It consists of two numbers, multiplied:
- tf—the frequency of a given term or word in a text, and
- idf—the logarithm of the total number of documents divided by the number of documents that contain that given term.
tf–idf is a measure of how frequently a word is used in the corpus. To be able to subdivide words into groups, it is important to understand not only which words appear in each text, but also which words appear frequently in one text but not at all in others.
The following figure shows some simple examples of these preprocessing techniques where the original text of the corpus is modified in order to generate a relevant and manageable list of words.
Now we’ll demonstrate how to apply some of these techniques in Python. Once we have our corpus represented mathematically, we need to identify the topics being discussed by applying unsupervised machine learning algorithms. In this case, “unsupervised” means that the algorithm doesn’t have any predefined topic labels, like “science fiction,” to apply to its output.
To cluster our corpus, we can choose from several algorithms, including non-negative matrix factorization (NMF), sparse principal components analysis (sparse PCA), and latent dirichlet allocation (LDA). We’ll focus on LDA because it is widely used by the scientific community due to its good results in social media, medical science, political science, and software engineering.
LDA is a model for unsupervised topic decomposition: It groups texts based on the words they contain and the probability of a word belonging to a certain topic. The LDA algorithm outputs the topic word distribution. With this information, we can define the main topics based on the words that are most likely associated with them. Once we have identified the main topics and their associated words, we can know which topic or topics apply to each text.
Consider the following corpus composed of five short sentences (all taken from New York Times headlines):
corpus = [ "Rafael Nadal Joins Roger Federer in Missing U.S. Open",
"Rafael Nadal Is Out of the Australian Open",
"Biden Announces Virus Measures",
"Biden's Virus Plans Meet Reality",
"Where Biden's Virus Plan Stands"]
The algorithm should clearly identify one topic related to politics and coronavirus, and a second one related to Nadal and tennis.
Applying the Strategy in Python
In order to detect the topics, we must import the necessary libraries. Python has some useful libraries for NLP and machine learning, including NLTK and Scikit-learn (sklearn).
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.decomposition import LatentDirichletAllocation as LDA
from nltk.corpus import stopwords
Using CountVectorizer(), we generate the matrix that denotes the frequency of the words of each text using CountVectorizer(). Note that the CountVectorizer allows for preprocessing if you include parameters such as stop_words to include the stop words, ngram_range to include n-grams, or lowercase=True to convert all characters to lowercase.
count_vect = CountVectorizer(stop_words=stopwords.words('english'), lowercase=True)
x_counts = count_vect.fit_transform(corpus)
x_counts.todense()
matrix([[0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0],
[1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1]], dtype=int64)
To define the vocabulary of our corpus, we can simply use the attribute .get_feature_names():
count_vect.get_feature_names()
['announces', 'australian', 'biden', 'federer', 'joins', 'measures', 'meet', 'missing', 'nadal', 'open', 'plan', 'plans', 'rafael', 'reality', 'roger', 'stands', 'virus']
Then, we perform the tf–idf calculations with the sklearn function:
tfidf_transformer = TfidfTransformer()
x_tfidf = tfidf_transformer.fit_transform(x_counts)
In order to perform the LDA decomposition, we have to define the number of topics. In this simple case, we know there are two topics or “dimensions.” But in general cases, this is a hyperparameter that needs some tuning, which could be done using algorithms like random search or grid search:
dimension = 2
lda = LDA(n_components = dimension)
lda_array = lda.fit_transform(x_tfidf)
lda_array
array([[0.8516198 , 0.1483802 ],
[0.82359501, 0.17640499],
[0.18072751, 0.81927249],
[0.1695452 , 0.8304548 ],
[0.18072805, 0.81927195]])
LDA is a probabilistic method. Here we can see the probability of each of the five headlines belonging to each of the two topics. We can see that the first two texts have a higher probability of belonging to the first topic and the next three to the second topic, as expected.
Finally, if we want to understand what these two topics are about, we can see the most important words in each topic:
components = [lda.components_[i] for i in range(len(lda.components_))]
features = count_vect.get_feature_names()
important_words = [sorted(features, key = lambda x: components[j][features.index(x)], reverse = True)[:3] for j in range(len(components))]
important_words
[['open', 'nadal', 'rafael'],
['virus', 'biden', 'measures']]
As expected, LDA correctly assigned words related to tennis tournaments and Nadal to the first topic and words related to Biden and virus to the second topic.
Large-scale Analyses and Real-world Use Cases
A large-scale analysis of topic modeling can be seen in this paper; I studied the main news topics during the 2016 US presidential election and observed the topics some mass media—like the New York Times and Fox News—included in their coverage, such as corruption and immigration. In this paper, I also analyzed the correlations and causations between mass media content and the election results.
Topic modeling is also widely used outside academia to discover hidden topical patterns present in big collections of texts. For example, it can be used in recommendation systems or to determine what customers/users are talking about in surveys, in feedback forms, or on social media.
The Toptal Engineering Blog extends its gratitude to Juan Manuel Ortiz de Zarate for reviewing the code samples presented in this article.
Recommended Reading on Topic Modeling
Improved Topic Modeling in Twitter
Albanese, Federico and Esteban Feuerstein. “Improved Topic Modeling in Twitter Through Community Pooling.” (December 20, 2021): arXiv:2201.00690 [cs.IR]
Analyzing Twitter for Public Health
Paul, Michael and Mark Dredze. “You Are What You Tweet: Analyzing Twitter for Public Health.” August 3, 2021.
Classifying Political Orientation on Twitter
Cohen, Raviv and Derek Ruths. “Classifying Political Orientation on Twitter: It’s Not Easy!” August 3, 2021.
Using Relational Topic Models to Capture Coupling
Gethers, Malcolm and Denis Poshyvanyk. “Using Relational Topic Models to Capture Coupling Among Classes in Object-oriented Software Systems.” October 25, 2010.
Further Reading on the Toptal Blog:
Understanding the basics
What is topic modeling in Python?
Topic modeling uses statistical and machine learning models to automatically detect topics in text documents.
What is topic modeling used for?
Topic modeling is used for different tasks, such as detecting trends and news on social media, detecting fake users, personalizing message recommendations, and characterizing information flow.
Is topic modeling supervised or unsupervised?
There are multiple supervised and unsupervised topic modeling techniques. Some use a labeled document data set to classify articles. Others analyze the frequency with which words appear to infer the latent topics in a corpus.
Is topic modeling the same as text classification?
No, they’re different. Text classification is a supervised learning task that categorizes texts into predefined groups. In contrast, topic modeling does not necessarily need a labeled data set.
Federico Albanese
Buenos Aires, Argentina
Member since January 9, 2019
About the author
Federico is a developer and data scientist who has worked at Facebook, where he made machine learning model predictions. He is a Python expert and a university lecturer. His PhD research pertains to graph machine learning.
Expertise
PREVIOUSLY AT