Getting to the Greeks: The Comprehensive Guide to Option Pricing

Option grants have grown even more common as a form of compensation, considering the proliferation of startups in the technology and life-sciences spaces. Their pricing, however, is widely misunderstood and many employees see options as a confusing ticket towards future wealth.

There are consequences to not setting the price of options at or near fair market value (FMV) at the time of grant, like IRC 409A in the United States which imposes a penal tax rate on options granted below FMV.

In light of this, I’ve written this article to cover the basics of option pricing, to make it as widely useful as possible, it’s not bound to any specific tax code or jurisdiction. The principles discussed primarily apply to traded options on listed stock but many of the heuristics can be applied to non-traded options or options on non-traded stock.

Basics of Options Valuation

Value of Options at Expiry

Options, which come in the form of calls and puts, grant a right, but not an obligation to a buyer. As a result, plain vanilla options can be worth something or nothing at expiry; they cannot be worth a negative value to a buyer since there are no net cash outflows after purchase. A seller of plain vanilla options is on the opposite side of the trade and can only lose as much as the buyer gains. It is a zero-sum game when this is the only transaction.

Modeling Calls

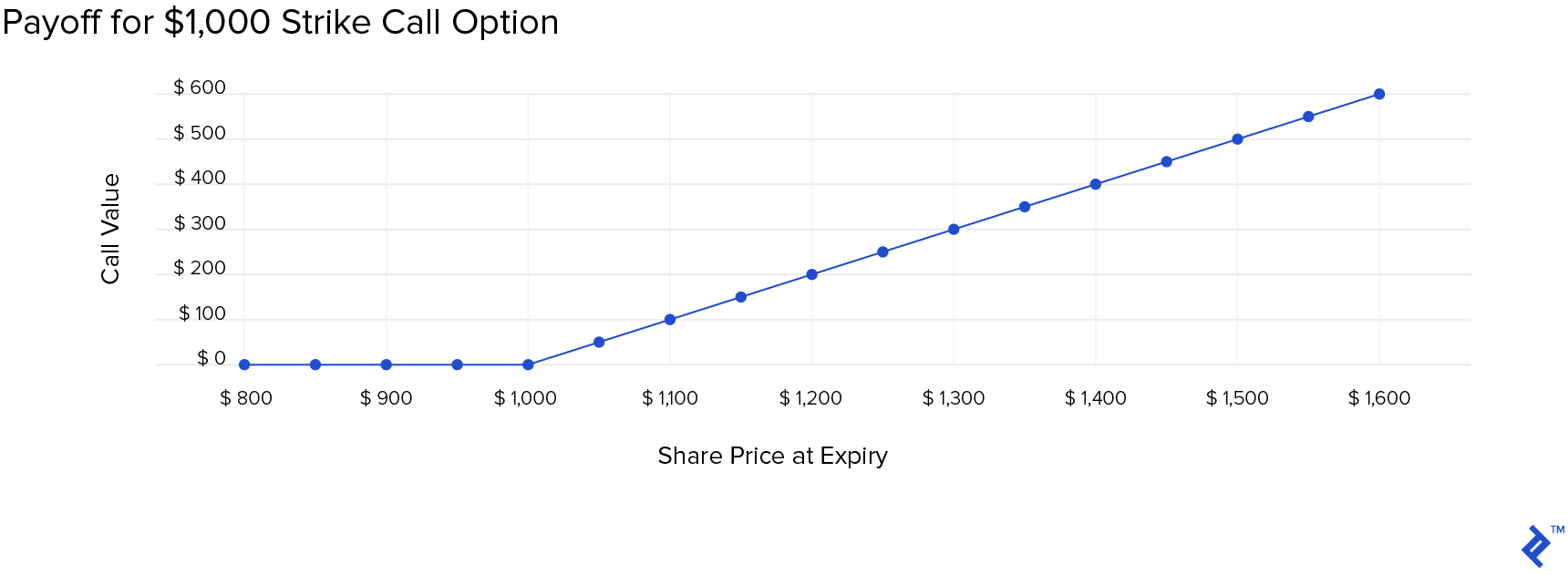
A call on a stock grants a right, but not an obligation to purchase the underlying at the strike price. If the spot price is above the strike, the holder of a call will exercise it at maturity. The payoff (not profit) at maturity can be modeled using the following call option formula and plotted in a chart.

Excel formula for a Call: = MAX (0, Share Price - Strike Price)

Modeling Puts

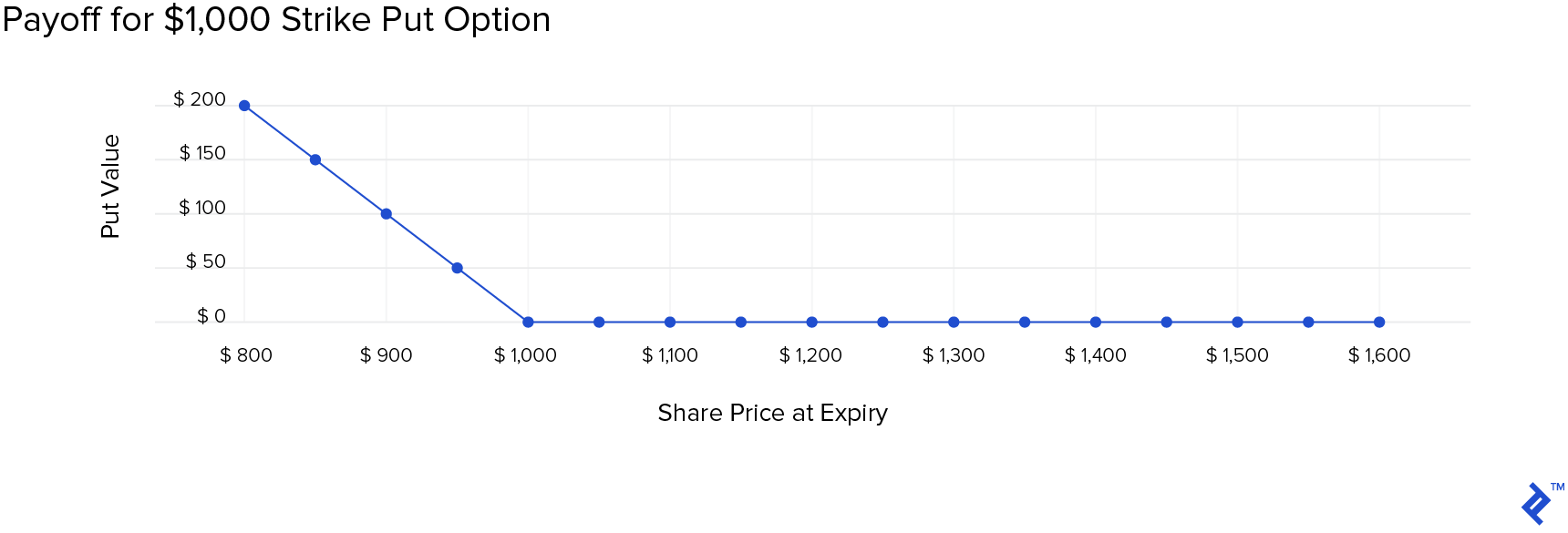
In the same way, a put which gives the right to sell at strike price can be modeled as below.

Excel formula for a Put: = MAX(0, Strike Price - Share Price)

Moneyness of an Option and Its Relevance

Based on the strike price and stock price at any point of time, the option pricing may be in, at, or out of the money:

• When the strike and stock prices are the same, the option is at-the-money.
• When the strike of a call is below the stock price, it is in-the-money (reverse for a put).
• When the strike of a call is above the stock price (reverse for a put), it is out-of-the-money.

Out-of-the-money and at-the-money options don’t have any intrinsic value to them but may have a time value before maturity. The distinction of moneyness is relevant since options trading exchanges have rules on automatic exercise at expiration based on whether an option is in-the-money or not. For instance:, the CBOE’s rules are:

The Options Clearing Corporation has provisions for the automatic exercise of certain in-the-money options at expiration, a procedure also referred to as exercise by exception. Generally, OCC will automatically exercise any expiring equity call or put in a customer account that is $0.01 or more in-the-money, and an index option that is $0.01 or more in-the-money. However, a specific brokerage firm’s threshold for such automatic exercise may or may not be the same as OCC’s.

The option pricing will hence depend on whether the spot price at expiry is above or below the strike price. Intuitively, the value of an option prior to expiry will be based on some measure of the probability of it being in-the-money with the cash flow discounted at an appropriate interest rate.

Black-Scholes-Merton (BSM) Option Valuation Model

Though options have been in use since the historical period of Greek, Roman and Phoenician civilizations, Fisher Black originally came up with this option pricing model in 1973, extensively used now, linking it to the derivation of heat-transfer formula in physics. The modifications to the model by Scholes and Merton evolved it into the Black-Scholes-Merton model. The formula looks as follows:

• Calls: \(C_t = S_t e^{- \delta T} N \left (d_1 \right ) - K e^{ \left (- r T \right)} N \left (d_2 \right )\)
• Puts: \(p_t = K e^{ \left (- r T \right )} N(d_2) - S_t e^{- \delta T} N(- d_1)\)
• \(d_1 = \ln\left ( \frac{S_0}{K} \right ) + \left ( r + \frac{\sigma ^2}{2} \right )\left ( \frac{T}{\sigma \sqrt{T}} \right )\)
• \(d_2 = d_1 - \sigma \sqrt{T}\)

Let’s not get overwhelmed by these elaborate put and call price formulas and first understand what the model is actually showing. For calls, their value before maturity will depend on the spot price of the underlying stock and its discounted value, then the strike price and its discounted value and finally, some measure of probability. The components of this break down as follows:

• \(e^{ \left ( - r T \right )}\) and \(e^{- \delta T}\) are ways of applying continuous compounding to a cash outflow and cash inflow from exercising the option.
• K and S are the strike and spot prices, respectively.

The remainder of the calculation is all about discounting the cash outflow at a continuously compounded discount rate, adjusting for any dividends, or cash flows before maturity and, for probability using a normal distribution.

Probability Assumptions

The BSM model assumes a normal distribution (bell-curve distribution or Gaussian distribution) of continuously compounded returns. The model also implies that as the ratio of current stock price to exercise price increases, the probability of exercising the call option increases, taking N(d) factors closer to 1, and implying that the uncertainty of not exercising the option decreases. As the N(d) factors get closer to 1, the result of the formula gets closer to the value of the intrinsic value of the call option. The other implication is that when variance (σ) increases, N(d) factors diverge and make the call option more valuable.

N(D2) is the probability that stock price is above the strike price at maturity. N(D1) is the term for calculating the expected value of cash/stock inflow at maturity only if the stock price is above the strike price. N(D1) is a conditional probability.

A gain for the call buyer occurs from two factors occurring at maturity:

1. The spot has to be above strike price. (Direction).
2. The difference between spot and strike prices at maturity (Quantum).

Imagine, a call at strike price $100. If the spot price of the stock is $101 or $150, the first condition is satisfied. The second condition is about whether the gain is $1 or $50. The term D1 combines these two into a conditional probability that if the spot at maturity is above strike, what will be its expected value in relation to current spot price.

Setting Up the BSM Model in Excel

The following model is what I use in Excel for BSM calculations (the shaded cells are calculations linked to other cells):

The formula for this is as follows:

Cell B2 = Valuation Date Cell B3 = Stock/Spot Price Cell B4 = Strike Price Cell B5 = Implied Volatility Cell B6 = Risk-free rate annualized Cell B7 = Time to expiration in years (Calculated as (B10-B2)/365) Cell B8 = Dividend yield (Calculated as B11/B3) Cell B9 = No. of options (set it to 1, for calculating the value not based on a contract) Cell B10 = Expiry date Cell B11 = Annual Dividend in currency terms Cell B13 = D1 =(LN((B3\EXP(-B8\B7))/B4)+((B6+((B5)^2)/2)\B7)) / ((B5)\SQRT(B7)) Cell B14 = D2 = B13-B5SQRT(B7) Cell B15 = N(D1) = NORMSDIST(B13) Cell B16 = N(D2) = NORMSDIST(B14) Cell B17 = Call = (B3\EXP(-B8\B7))\B15-B4\EXP(-B6\B7)\B16 Cell B18 = Put = (B17-(B3\EXP(-B8\B7))+B4\EXP(-B6\B7)

Cash Flows of the Underlying

A call lets the buyer enjoy the upside of a stock without really holding it for a period till expiry. Intuitively, if the upside is paid out during the period of holding, then the calls should be less valuable since the right to that upside is not being derived by the option holder. Of course, the reverse applies in the case of puts. This intuition can be seen in the following graphs for a dividend paying stock with 0%, 2%, and 5% dividend. The model assumes that dividends are also paid out at a continuously compounded rate.

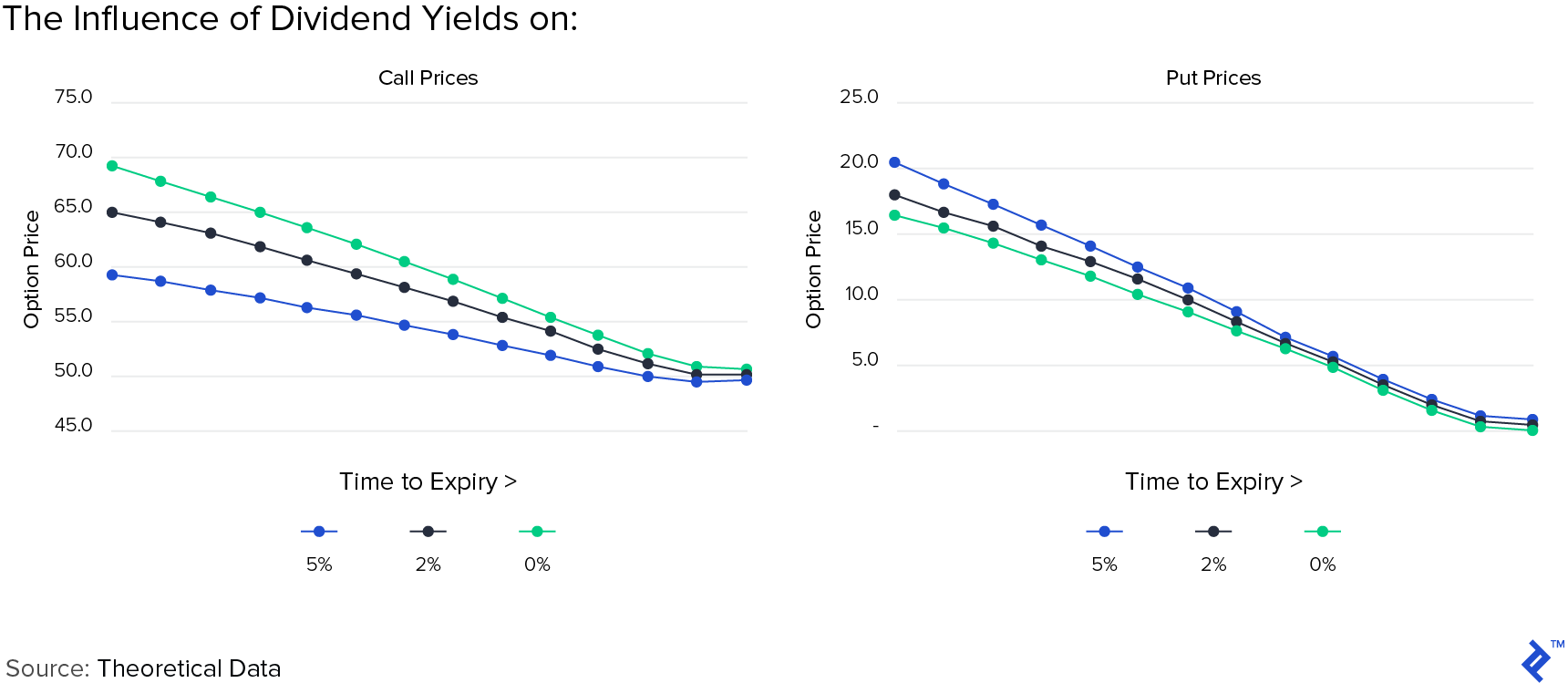
Now that special dividends are being discussed due to changes in the US tax code, it is worth mentioning that you will see an adjustment factor to traded options for one-time dividends above a certain percentage of the stock price. One-time special dividends have a big impact on option pricing. In 2004, when MSFT announced an additional one-time special dividend of $3 per share against its normal $0.08 quarterly, the options were adjusted.

Sensitivity to Factors or Option Greeks

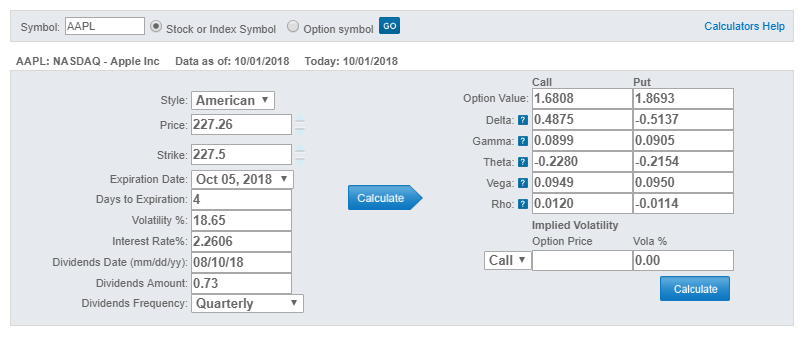
Options Industry Council (OIC) has a free calculator which will display the traded option values and the greeks. I have analyzed the values for AAPL from 1st October 2018 from the Options Industry Council’s website.

Delta and Gamma or Spot Price

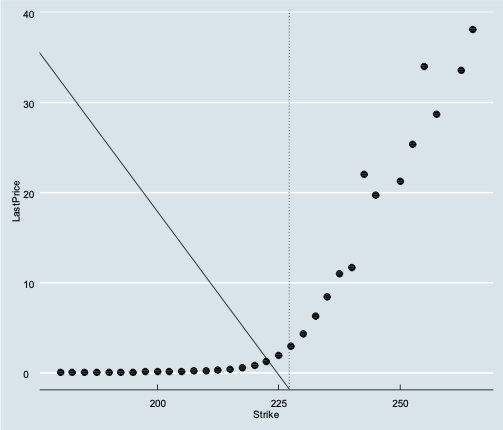
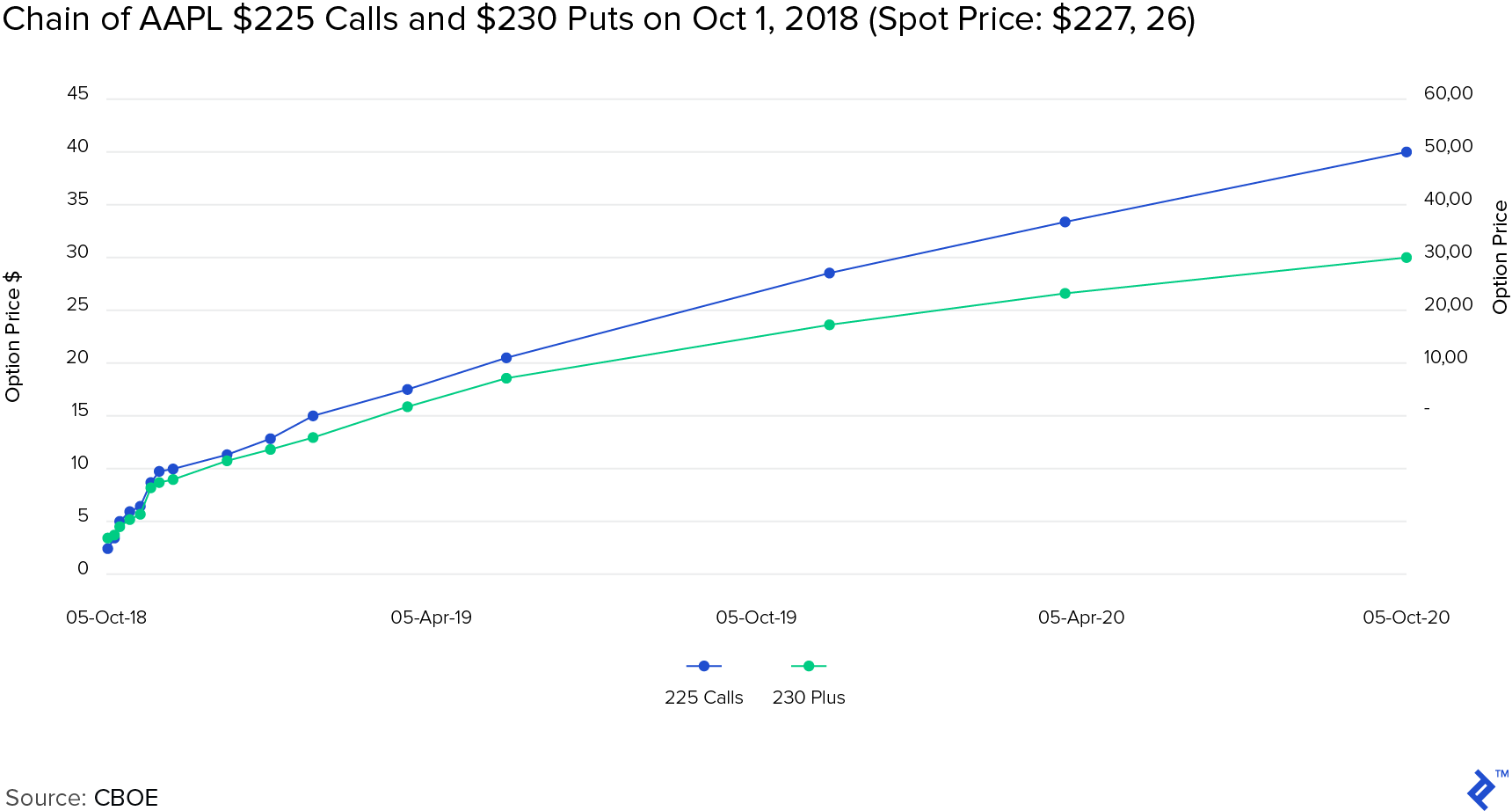
The following graph is for AAPL Puts expiring Oct 12,2018 on Oct 01, 2018 with the vertical line indicating last price.

The following is for AAPL Calls expiring Oct 12,2018 on Oct 01,2018.

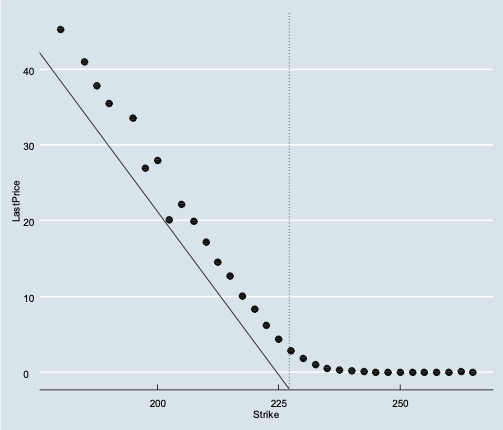
The last traded call and put option prices are clearly correlated to the strike price and form this hockey stick-esque graph. The reason the dots don’t align to a line is because some of the options were not traded on Oct 1 and the last traded price of these options are older, especially for deep in-the-money options.

What happens when the spot price changes for AAPL? AAPL’s price changes by nanoseconds at the exchange. Intuitively, and based on the BSM model the option pricing also should change too. This is measured by Delta, which is the approximation of how the value of an option changes for a change in spot price. It is an approximate value of how much the option value moves for a change in $1 of the underlying.

Delta is used as a hedging ratio. If you are looking to hedge an underlying position with an option that has a delta of 0.5, you will need two options (2 x 0.5) to completely hedge the position (and make it delta-neutral). Delta is an approximation, though. It works well for a small movement in price and for short periods of time. We see the relationship of the call to changes in stock price below as well as the change in delta over the same range of stock prices. The call prices don’t move smoothly as a line and consequently, the calculated delta moves like a curve. This becomes more noticeable nearer to the strike price.

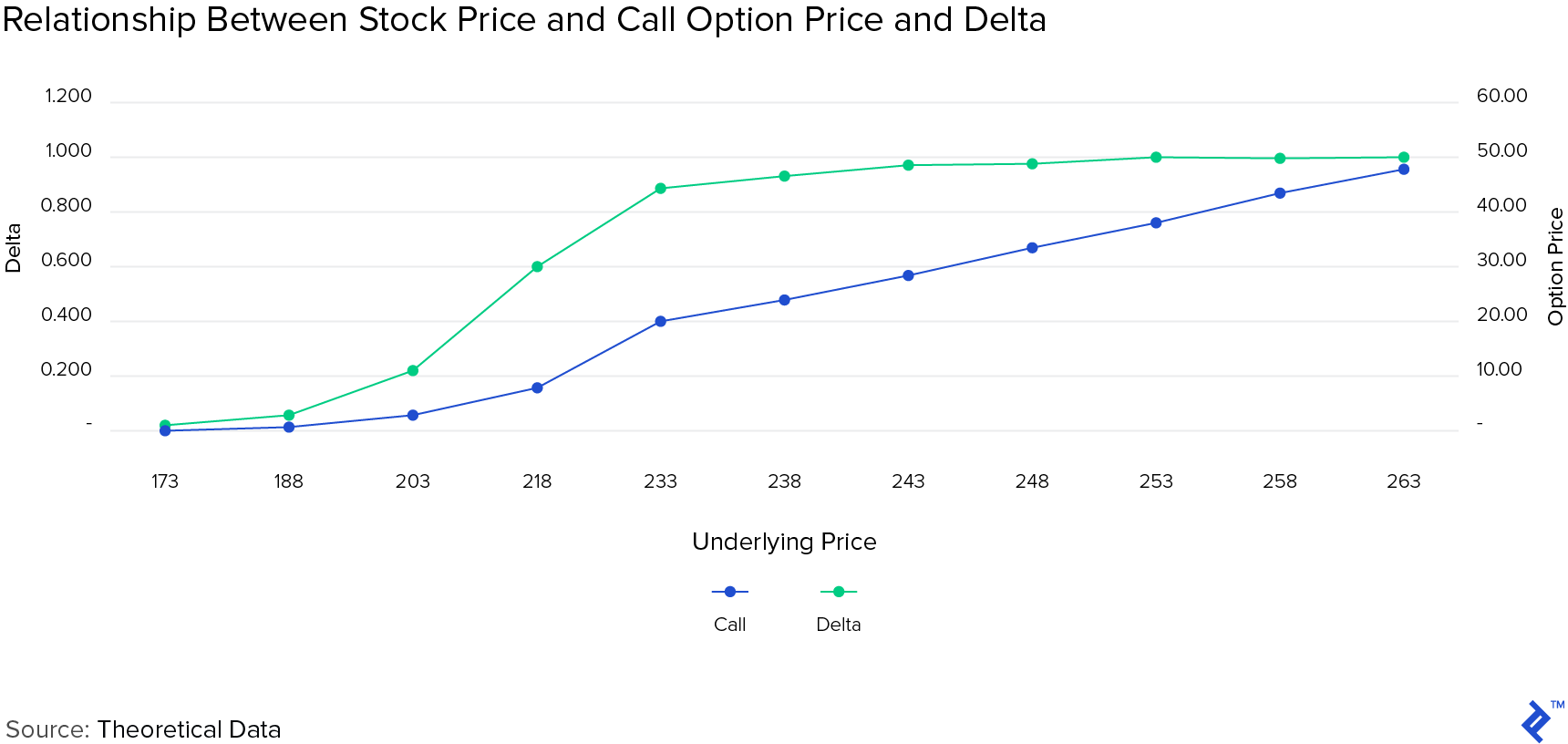
The change in delta for a change is $1 value of the underlying is called Gamma. Gamma is always a positive value and Delta is positive for a call and negative for a put (for the buyer). It also means that for a call, the highest % change will happen when it turns from being out-of-the-money to in-the-money, or vice-versa. Gamma or the rate of change in delta approaches zero as the strike price moves away from the spot price (for deep out-of-the-money or in-the-money option positions).

Theta, or Time Value

An option’s price depends on how long it has to run to expiry. Intuitively, the longer the time to expiry, the higher the likelihood that it will end up in-the-money. Hence, longer dated options tend to have higher values, regardless of whether they are puts or calls. The time value subsequently decays to 0 as it nears expiry.

The rate of decay is not a straight line. It is easier to think of it using the analogy of a ball rolling down a slope. The speed picks up as the ball rolls further down the slope—slowest being at the top and fastest at the bottom (at expiry). The rate of decay is represented by Theta and is positive for calls and puts.

Rho or Interest Rates

Interest rates have an impact on option value through the use as a discount rate. Intuitively, calls imply getting the upside of holding the underlying shares without dishing out the full price. Because a call buyer doesn’t need to purchase the full price of the stock, the difference between the full stock price and the call option could theoretically be invested and therefore, the call option should have a higher value for higher discount rates. The sensitivity to interest rates is measured by Rho, with higher interest rates increasing the value of calls and vice-versa for puts.

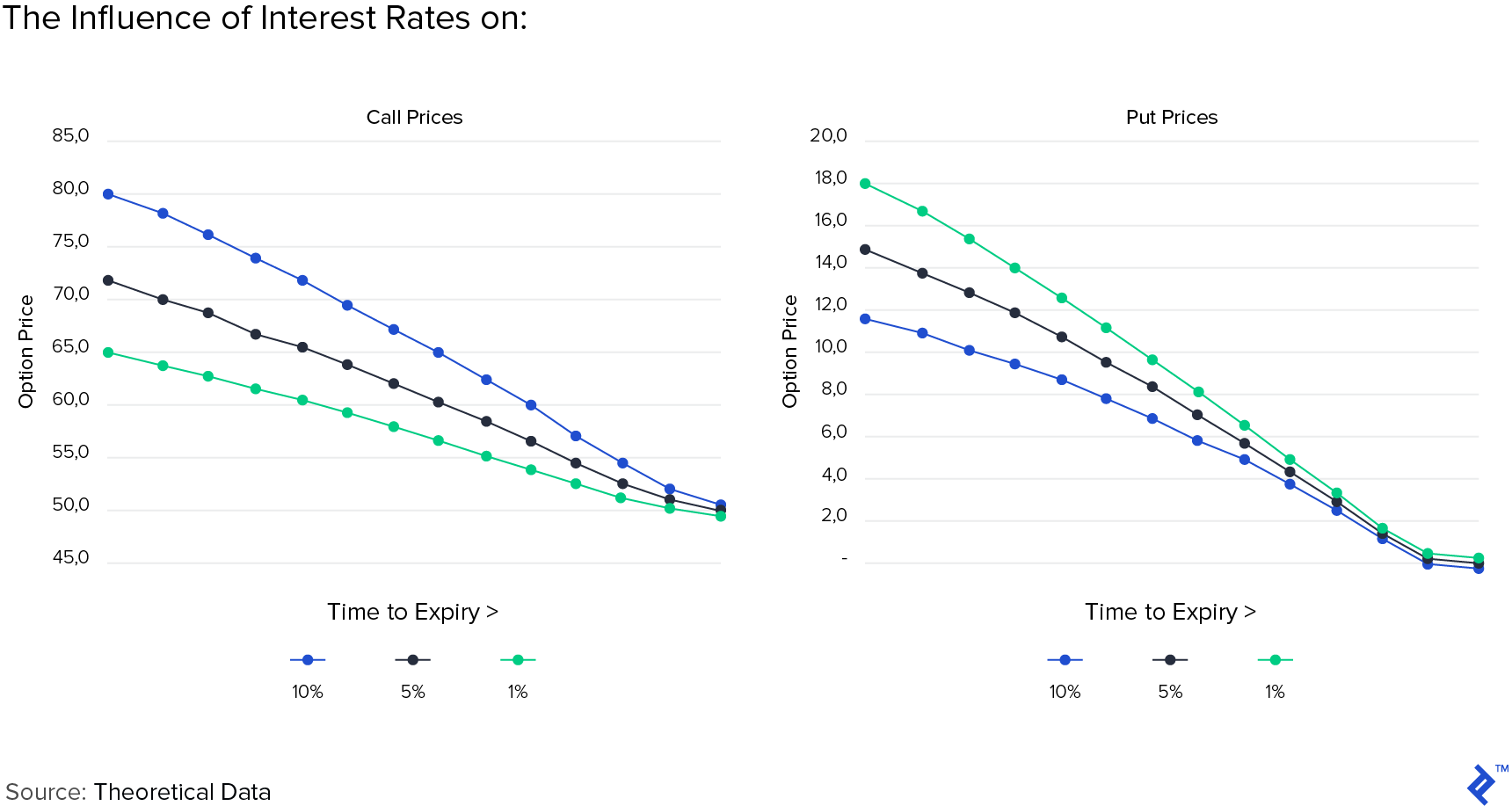
Vega or Volatility

Vega, though not actually in the Greek alphabet, is used to denote the sensitivity of option value to volatility. Volatility refers to the possible magnitude of price moves up or down. The higher the volatility from a spot price, the higher the likelihood that the price may reach the strike. Hence, the higher the volatility, the higher the price of options.

Volatility is usually back filled using implied volatility (I”). Implied volatility is calculated with the BSM Model, using the traded prices of options. IV has become a traded asset class by itself in through VIX options.

If you buy an option in a very calm market and there is a sudden uptick and downtick in the price of the underlying, with the price ending back where it was before, you may see that option pricing has increased in value. This is from a revision of its IV estimate.

To summarize the effect of Vega, and indeed the other Greeks, on the prices of options please refer to the following table.

Put-call Parity and Use Cases

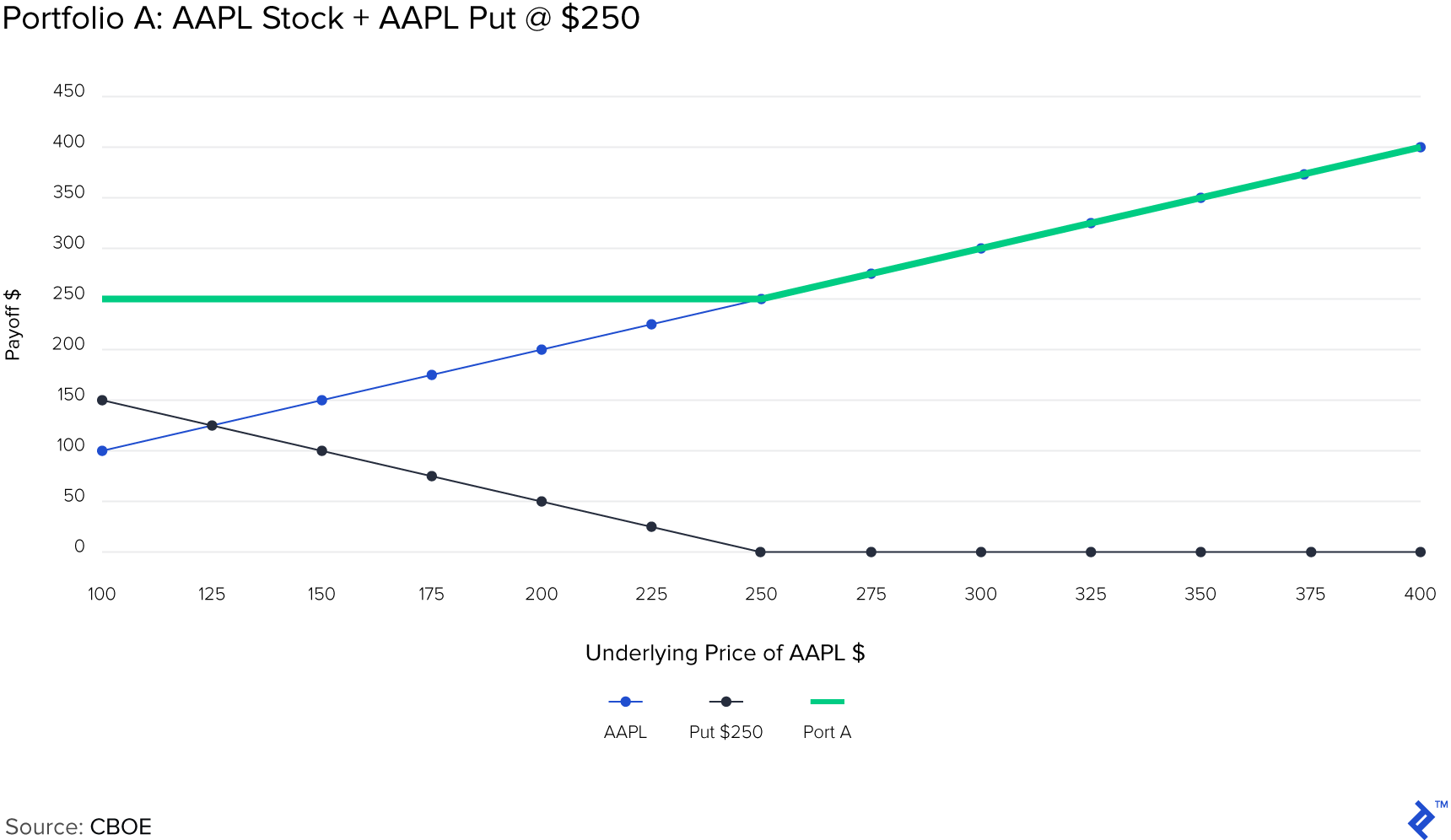
Imagine that you have a portfolio, creatively named “A”, which has only a European call on AAPL at strike $250 expiring on Dec 21, 2018, and one share of the underlying APPL stock:

Then you create another portfolio, “B”, which has only a European call on AAPL at strike $250 expiring on Dec 21, 2018, and a US government T-bill maturing on the same day for a maturity value of $250.

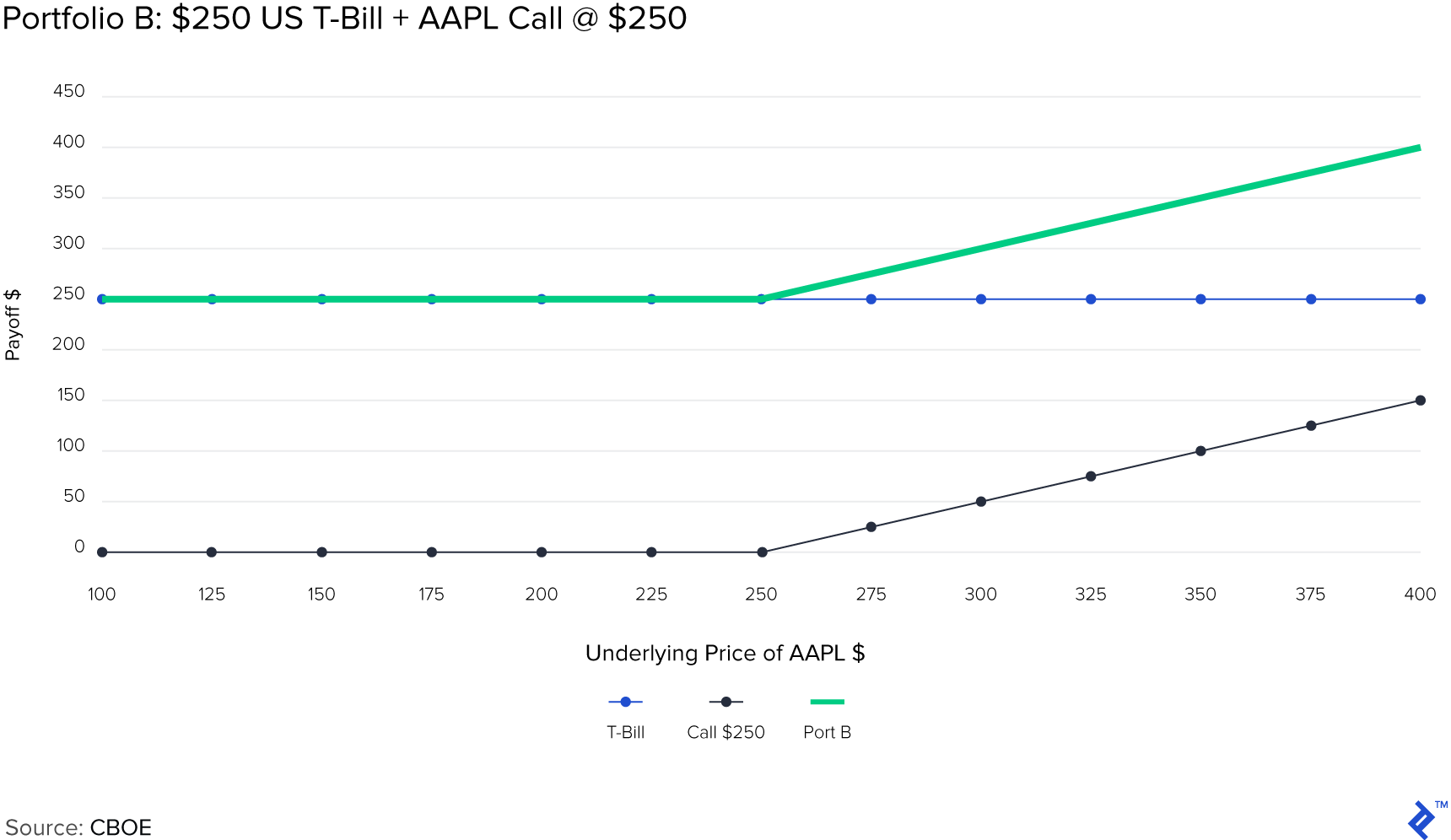
As you can see, both portfolio A and portfolio B have the same payoff at expiry. This principle is called put-call parity. Another way of stating it is:

This equation can be rearranged to mimic other positions:

1. Hold the underlying and a put, by borrowing funds at risk-free rate and you have created a synthetic call.
2. Short the underlying while owning a T-bill and a call and you have a synthetic put.
3. If you want to earn treasury (i.e., risk-free) rates while holding an underlying stock, then hold the put and short the call.
4. You can also mimic holding the underlying by holding a call, shorting a put and holding a T-bill.

This will only work with European-style expiration, calls, and puts at the same strike price.

Employee Non-traded Options

The employee stock options for non-traded companies are different from exchange-traded options in a manner of different ways:

1. There is no automatic exercise when it is in-the-money.
2. Vesting requirements restrict liquidity.
3. Counterparty risk is higher, as you are dealing directly with a private corporation, over a collateralized exchange.
4. Portfolio concentration is also more extreme, as there are fewer diversification measures available.

In addition to these, as we know, valuation is also a completely different ball game for private companies. As we discussed, delta (stock price), theta (time value), rho (rate of interest) and vega (volatility) are important determinants of options valuation. These make valuation of employee stock options more challenging, since Delta, Gamma and Volatility are especially hard to determine, since the stock itself may not be traded.

For an employee holding stock options, the key factors to keep in mind are that:

1. Volatility has a key impact on valuation.
2. Option decay due to time value is not linear in nature. Remember the ball rolling down the hill analogy.
3. Option valuation is both intrinsic value and time value. Just because there is no intrinsic value doesn’t mean that the option is worthless, time heals all wounds and may also close the gap. When you receive an option grant, it is usually at-the-money or may be out-of-the-money, with no intrinsic value. Tracking intrinsic value as the stock rises is intuitive, but time value, the opportunity cost of an early exercise, is not always intuitive or accounted for. Due to this opportunity cost, you should exercise an option early only for a few valid reasons such as the need for a cash flow, portfolio diversification or stock outlook.

Parting Thoughts and Glossary

Options are not that complicated when you understand their components. Think of them as more flexible building blocks for allowing you to construct and manage financial portfolios in a less capital intensive way. Understanding the implications of the greeks is the first step towards comprehending their behavior.

As a brief glossary, below are some key terms mentioned throughout the article, summarized in a concise manner:

• Calls and puts – Call is an option with no obligation to buy the underlying asset at an agreed price on or before a specified date. Put is an option with no obligation to sell the underlying asset at an agreed price on or before a specified date.
• Premium – Price paid by a purchaser to the seller (writer) of an option is called a premium. It is the valuation of an option at the time of the trade.
• Exercise/strike and spot prices – Exercise or strike price is the specified price for buying/selling an underlying asset using an option. The spot price is the price of the underlying asset in the spot market.
• Payoff – The net cash flow on expiry of an option. One of the cash flows is the exercise price and the other is the market value of the asset.
• European and American exercise – European style option can only be exercised at a specified period prior to expiration. American option can be exercised anytime at or prior to the expiry.
• Time value and intrinsic value – The time value is the premium at a time minus the intrinsic value. The intrinsic value of an option is the difference between the strike price and the spot price at any time.