Maximum Flow and the Linear Assignment Problem
The Hungarian graph algorithm solves the linear assignment problem in polynomial time. By modeling resources (e.g., contractors and available contracts) as a graph, the Hungarian algorithm can be used to efficiently determine an optimum way of allocating resources.
The Hungarian graph algorithm solves the linear assignment problem in polynomial time. By modeling resources (e.g., contractors and available contracts) as a graph, the Hungarian algorithm can be used to efficiently determine an optimum way of allocating resources.
Dmitri has a PhD in computer science from UC Irvine and works primarily in UNIX/Linux ecosystems. He specializes in Python and Java.
PREVIOUSLY AT

Here’s a problem: Your business assigns contractors to fulfill contracts. You look through your rosters and decide which contractors are available for a one month engagement and you look through your available contracts to see which of them are for one month long tasks. Given that you know how effectively each contractor can fulfill each contract, how do you assign contractors to maximize the overall effectiveness for that month?
This is an example of the assignment problem, and the problem can be solved with the classical Hungarian algorithm.

The Hungarian algorithm (also known as the Kuhn-Munkres algorithm) is a polynomial time algorithm that maximizes the weight matching in a weighted bipartite graph. Here, the contractors and the contracts can be modeled as a bipartite graph, with their effectiveness as the weights of the edges between the contractor and the contract nodes.
In this article, you will learn about an implementation of the Hungarian algorithm that uses the Edmonds-Karp algorithm to solve the linear assignment problem. You will also learn how the Edmonds-Karp algorithm is a slight modification of the Ford-Fulkerson method and how this modification is important.
The Maximum Flow Problem
The maximum flow problem itself can be described informally as the problem of moving some fluid or gas through a network of pipes from a single source to a single terminal. This is done with an assumption that the pressure in the network is sufficient to ensure that the fluid or gas cannot linger in any length of pipe or pipe fitting (those places where different lengths of pipe meet).
By making certain changes to the graph, the assignment problem can be turned into a maximum flow problem.
Preliminaries
The ideas needed to solve these problems arise in many mathematical and engineering disciplines, often similar concepts are known by different names and expressed in different ways (e.g., adjacency matrices and adjacency lists). Since these ideas are quite esoteric, choices are made regarding how generally these concepts will be defined for any given setting.
This article will not assume any prior knowledge beyond a little introductory set theory.
The implementations in this post represent the problems as directed graphs (digraph).
Digraphs
A digraph has two attributes, setOfNodes and setOfArcs. Both of these attributes are sets (unordered collections). In the code blocks on this post, I’m actually using Python’s frozenset, but that detail isn’t particularly important.
DiGraph = namedtuple('DiGraph', ['setOfNodes','setOfArcs'])
(Note: This, and all other code in this article, are written in Python 3.6.)
Nodes
A node n is composed of two attributes:
-
n.uid: A unique identifier.This means that for any two nodes
xandy,
x.uid != y.uid
-
n.datum: This represents any data object.
Node = namedtuple('Node', ['uid','datum'])
Arcs
An arc a is composed of three attributes:
-
a.fromNode: This is a node, as defined above. -
a.toNode: This is a node, as defined above. -
a.datum: This represents any data object.
Arc = namedtuple('Arc', ['fromNode','toNode','datum'])
The set of arcs in the digraph represents a binary relation on the nodes in the digraph. The existence of arc a implies that a relationship exists between a.fromNode and a.toNode.
In a directed graph (as opposed to an undirected graph), the existence of a relationship between a.fromNode and a.toNode does not imply that a similar relationship between a.toNode and a.fromNode exists.
This is because in an undirected graph, the relationship being expressed is not necessarily symmetric.
DiGraphs
Nodes and arcs can be used to define a digraph, but for convenience, in the algorithms below, a digraph will be represented using as a dictionary.
Here’s a method that can convert the graph representation above into a dictionary representation similar to this one:
def digraph_to_dict(G):
G_as_dict = dict([])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
pdg(G)
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
pdg(G)
raise KeyError(err_msg)
G_as_dict[a.fromNode] = (G_as_dict[a.fromNode].union(frozenset([a]))) if (a.fromNode in G_as_dict) else frozenset([a])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if a.toNode not in G_as_dict:
G_as_dict[a.toNode] = frozenset([])
return G_as_dict
And here’s another one that converts it into a dictionary of dictionaries, another operation that will be useful:
def digraph_to_double_dict(G):
G_as_dict = dict([])
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.fromNode not in G_as_dict):
G_as_dict[a.fromNode] = dict({a.toNode : frozenset([a])})
else:
if(a.toNode not in G_as_dict[a.fromNode]):
G_as_dict[a.fromNode][a.toNode] = frozenset([a])
else:
G_as_dict[a.fromNode][a.toNode] = G_as_dict[a.fromNode][a.toNode].union(frozenset([a]))
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if a.toNode not in G_as_dict:
G_as_dict[a.toNode] = dict({})
return G_as_dict
When the article talks about a digraph as represented by a dictionary, it will mention G_as_dict to refer to it.
Sometimes it’s helpful to fetch a node from a digraph G by it up through its uid (unique identifier):
def find_node_by_uid(find_uid, G):
nodes = {n for n in G.setOfNodes if n.uid == find_uid}
if(len(nodes) != 1):
err_msg = 'Node with uid {find_uid!s} is not unique.'.format(**locals())
raise KeyError(err_msg)
return nodes.pop()
In defining graphs, people sometimes use the terms node and vertex to refer to the same concept; the same is true of the terms arc and edge.
Two popular graph representations in Python are this one which uses dictionaries and another which uses objects to represent graphs. The representation in this post is somewhere in between these two commonly used representations.
This is my digraph representation. There are many like it, but this one is mine.
Walks and Paths
Let S_Arcs be a finite sequence (ordered collection) of arcs in a digraph G such that if a is any arc in S_Arcs except for the last, and b follows a in the sequence, then there must be a node n = a.fromNode in G.setOfNodes such that a.toNode = b.fromNode.
Starting from the first arc in S_Arcs, and continuing until the last arc in S_Arcs, collect (in the order encountered) all nodes n as defined above between each two consecutive arcs in S_Arcs. Label the ordered collection of nodes collected during this operation S_{Nodes}.
def path_arcs_to_nodes(s_arcs):
s_nodes = list([])
arc_it = iter(s_arcs)
step_count = 0
last = None
try:
at_end = False
last = a1 = next(arc_it)
while (not at_end):
s_nodes += [a1.fromNode]
last = a2 = next(arc_it)
step_count += 1
if(a1.toNode != a2.fromNode):
err_msg = "Error at index {step_count!s} of Arc sequence.".format(**locals())
raise ValueError(err_msg)
a1 = a2
except StopIteration as e:
at_end = True
if(last is not None):
s_nodes += [last.toNode]
return s_nodes
-
If any node appears more than once in the sequence
S_Nodesthen callS_Arcsa Walk on digraphG. -
Otherwise, call
S_Arcsa path fromlist(S_Nodes)[0]tolist(S_Nodes)[-1]on digraphG.
Source Node
Call node s a source node in digraph G if s is in G.setOfNodes and G.setOfArcs contains no arc a such that a.toNode = s.
def source_nodes(G):
to_nodes = frozenset({a.toNode for a in G.setOfArcs})
sources = G.setOfNodes.difference(to_nodes)
return sources
Terminal Node
Call node t a terminal node in digraph G if t is in G.setOfNodes and G.setOfArcs contains no arc a such that a.fromNode = t.
def terminal_nodes(G):
from_nodes = frozenset({a.fromNode for a in G.setOfArcs})
terminals = G.setOfNodes.difference(from_nodes)
return terminals
Cuts and s-t Cuts
A cut cut of a connected digraph G is a subset of arcs from G.setOfArcs which partitions the set of nodes G.setOfNodes in G. G is connected if every node n in G.setOfNodes and has at least one arc a in G.setOfArcs such that either n = a.fromNode or n = a.toNode, but a.fromNode != a.toNode.
Cut = namedtuple('Cut', ['setOfCutArcs'])
The definition above refers to a subset of arcs, but it can also define a partition of the nodes of G.setOfNodes.
For the functions predecessors_of and successors_of, n is a node in set G.setOfNodes of digraph G, and cut is a cut of G:
def cut_predecessors_of(n, cut, G):
allowed_arcs = G.setOfArcs.difference(frozenset(cut.setOfCutArcs))
predecessors = frozenset({})
previous_count = len(predecessors)
reach_fringe = frozenset({n})
keep_going = True
while( keep_going ):
reachable_from = frozenset({a.fromNode for a in allowed_arcs if (a.toNode in reach_fringe)})
reach_fringe = reachable_from
predecessors = predecessors.union(reach_fringe)
current_count = len(predecessors)
keep_going = current_count - previous_count > 0
previous_count = current_count
return predecessors
def cut_successors_of(n, cut, G):
allowed_arcs = G.setOfArcs.difference(frozenset(cut.setOfCutArcs))
successors = frozenset({})
previous_count = len(successors)
reach_fringe = frozenset({n})
keep_going = True
while( keep_going ):
reachable_from = frozenset({a.toNode for a in allowed_arcs if (a.fromNode in reach_fringe)})
reach_fringe = reachable_from
successors = successors.union(reach_fringe)
current_count = len(successors)
keep_going = current_count - previous_count > 0
previous_count = current_count
return successors
Let cut be a cut of digraph G.
def get_first_part(cut, G):
firstPartFringe = frozenset({a.fromNode for a in cut.setOfCutArcs})
firstPart = firstPartFringe
for n in firstPart:
preds = cut_predecessors_of(n,cut,G)
firstPart = firstPart.union(preds)
return firstPart
def get_second_part(cut, G):
secondPartFringe = frozenset({a.toNode for a in cut.setOfCutArcs})
secondPart = secondPartFringe
for n in secondPart:
succs= cut_successors_of(n,cut,G)
secondPart = secondPart.union(succs)
return secondPart
cut is a cut of digraph G if: (get_first_part(cut, G).union(get_second_part(cut, G)) == G.setOfNodes) and (len(get_first_part(cut, G).intersect(get_second_part(cut, G))) == 0) cut is called an x-y cut if (x in get_first_part(cut, G)) and (y in get_second_part(cut, G) ) and (x != y). When the node x in a x-y cut cut is a source node and node y in the x-y cut is a terminal node, then this cut is called a s-t cut.
STCut = namedtuple('STCut', ['s','t','cut'])
Flow Networks
You can use a digraph G to represent a flow network.
Assign each node n, where n is in G.setOfNodes an n.datum that is a FlowNodeDatum:
FlowNodeDatum = namedtuple('FlowNodeDatum', ['flowIn','flowOut'])
Assign each arc a, where a is in G.setOfArcs and a.datum that is a FlowArcDatum.
FlowArcDatum = namedtuple('FlowArcDatum', ['capacity','flow'])
flowNodeDatum.flowIn and flowNodeDatum.flowOut are positive real numbers.
flowArcDatum.capacity and flowArcDatum.flow are also positive real numbers.
For every node node n in G.setOfNodes:
n.datum.flowIn = sum({a.datum.flow for a in G.Arcs if a.toNode == n})
n.datum.flowOut = sum({a.datum.flow for a in G.Arcs if a.fromNode == n})
Digraph G now represents a flow network.
The flow of G refers to the a.flow for all arcs a in G.
Feasible Flows
Let digraph G represent a flow network.
The flow network represented by G has feasible flows if:
-
For every node
ninG.setOfNodesexcept for source nodes and terminal nodes :n.datum.flowIn = n.datum.flowOut. -
For every arc
ainG.setOfNodes:a.datum.capacity <= a.datum.flow.
Condition 1 is called a conservation constraint.
Condition 2 is called a capacity constraint.
Cut Capacity
The cut capacity of an s-t cut stCut with source node s and terminal node t of a flow network represented by a digraph G is:
def cut_capacity(stCut, G):
part_1 = get_first_part(stCut.cut,G)
part_2 = get_second_part(stCut.cut,G)
s_part = part_1 if stCut.s in part_1 else part_2
t_part = part_1 if stCut.t in part_1 else part_2
cut_capacity = sum({a.datum.capacity for a in stCut.cut.setOfCutArcs if ( (a.fromNode in s_part) and (a.toNode in t_part) )})
return cut_capacity
Minimum Capacity Cut
Let stCut = stCut(s,t,cut) be an s-t cut of a flow network represented by a digraph G.
stCut is the minimum capacity cut of the flow network represented by G if there is no other s-t cut stCutCompetitor in this flow network such that:
cut_capacity(stCut, G) < cut_capacity(stCutCompetitor, G)
Stripping the Flows Away
I would like to refer to the digraph that would be the result of taking a digraph G and stripping away all the flow data from all the nodes in G.setOfNodes and also all the arcs in G.setOfArcs.
def strip_flows(G):
new_nodes= frozenset( (Node(n.uid, FlowNodeDatum(0.0,0.0)) for n in G.setOfNodes) )
new_arcs = frozenset([])
for a in G.setOfArcs:
new_fromNode = Node(a.fromNode.uid, FlowNodeDatum(0.0,0.0))
new_toNode = Node(a.toNode.uid, FlowNodeDatum(0.0,0.0))
new_arc = Arc(new_fromNode, new_toNode, FlowArcDatum(a.datum.capacity, 0.0))
new_arcs = new_arcs.union(frozenset([new_arc]))
return DiGraph(new_nodes, new_arcs)
Maximum Flow Problem
A flow network represented as a digraph G, a source node s in G.setOfNodes and a terminal node t in G.setOfNodes, G can represent a maximum flow problem if:
(len(list(source_nodes(G))) == 1) and (next(iter(source_nodes(G))) == s) and (len(list(terminal_nodes(G))) == 1) and (next(iter(terminal_nodes(G))) == t)
Label this representation:
MaxFlowProblemState = namedtuple('MaxFlowProblemState', ['G','sourceNodeUid','terminalNodeUid','maxFlowProblemStateUid'])
Where sourceNodeUid = s.uid, terminalNodeUid = t.uid, and maxFlowProblemStateUid is an identifier for the problem instance.
Maximum Flow Solution
Let maxFlowProblem represent a maximum flow problem. The solution to maxFlowProblem can be represented by a flow network represented as a digraph H.
Digraph H is a feasible solution to the maximum flow problem on input python maxFlowProblem if:
-
strip_flows(maxFlowProblem.G) == strip_flows(H). -
His a flow network and has feasible flows.
If in addition to 1 and 2:
- There can be no other flow network represented by digraph
Ksuch thatstrip_flows(G) == strip_flows(K)andfind_node_by_uid(t.uid,G).flowIn < find_node_by_uid(t.uid,K).flowIn.
Then H is also an optimal solution to maxFlowProblem.
In other words a feasible maximum flow solution can be represented by a digraph, which:
-
Is identical to digraph
Gof the corresponding maximum flow problem with the exception that then.datum.flowIn,n.datum.flowOutand thea.datum.flowof any of the nodes and arcs may be different. -
Represents a flow network that has feasible flows.
And, it can represent an optimal maximum flow solution if additionally:
- The
flowInfor the node corresponding to the terminal node in the maximum flow problem is as large as possible (when conditions 1 and 2 are still satisfied).
If digraph H represents a feasible maximum flow solution : find_node_by_uid(s.uid,H).flowOut = find_node_by_uid(t.uid,H).flowIn this follows from the max flow, min cut theorem (discussed below). Informally, since H is assumed to have feasible flows this means that flow can neither be ‘created’ (except at source node s) nor ‘destroyed’ (except at terminal node t) while crossing any (other) node (conservation constraints).
Since a maximum flow problem contains only a single source node s and a single terminal node t, all flow ‘created’ at s must be ‘destroyed’ at t or the flow network does not have feasible flows (the conservation constraint would have been violated).
Let digraph H represent a feasible maximum flow solution; the value above is called the s-t Flow Value of H.
Let:
mfps=MaxFlowProblemState(H, maxFlowProblem.sourceNodeUid, maxFlowProblem.terminalNodeUid, maxFlowProblem.maxFlowProblemStateUid)
This means that mfps is a successor state of maxFlowProblem, which just means that mfps is exacly like maxFlowProblem with the exception that the values of a.flow for arcs a in maxFlowProblem.setOfArcs may be different than a.flow for arcs a in mfps.setOfArcs.
def get_mfps_flow(mfps):
flow_from_s = find_node_by_uid(mfps.sourceNodeUid,mfps.G).datum.flowOut
flow_to_t = find_node_by_uid(mfps.terminalNodeUid,mfps.G).datum.flowIn
if( (flow_to_t - flow_from_s) > 0):
raise Exception('Infeasible s-t flow')
return flow_to_t
Here’s a visualization of a mfps along with its associated maxFlowProb. Each arc a in the image has a label, these labels are a.datum.flowFrom / a.datum.flowTo, each node n in the image has a label, and these labels are n.uid {n.datum.flowIn / a.datum.flowOut}.
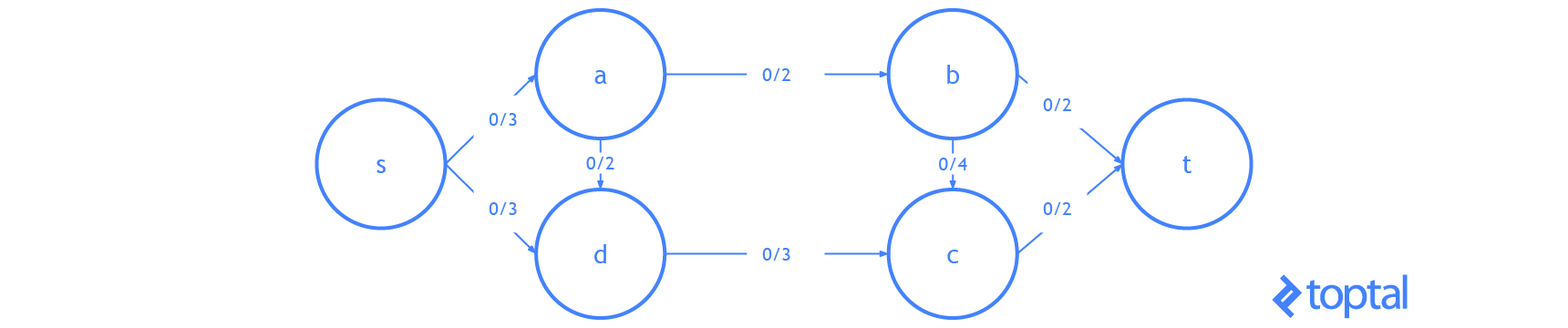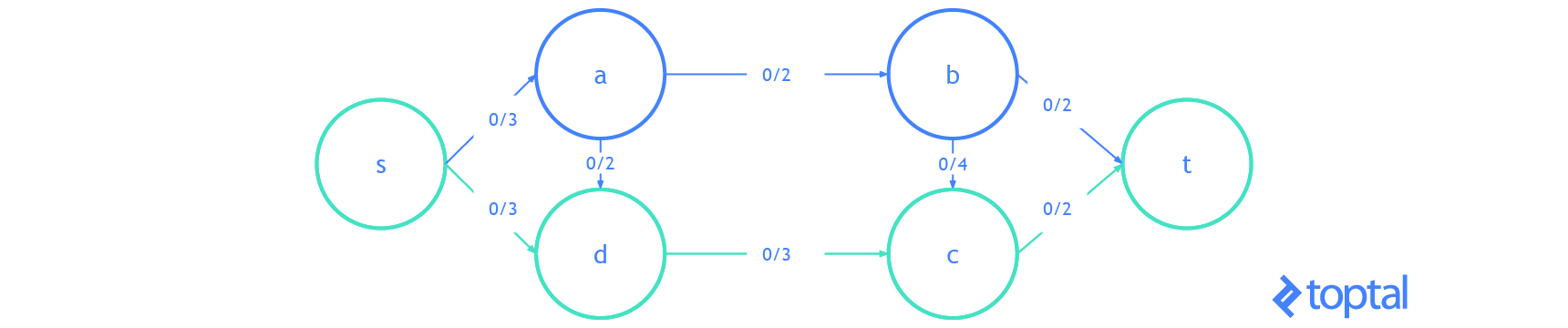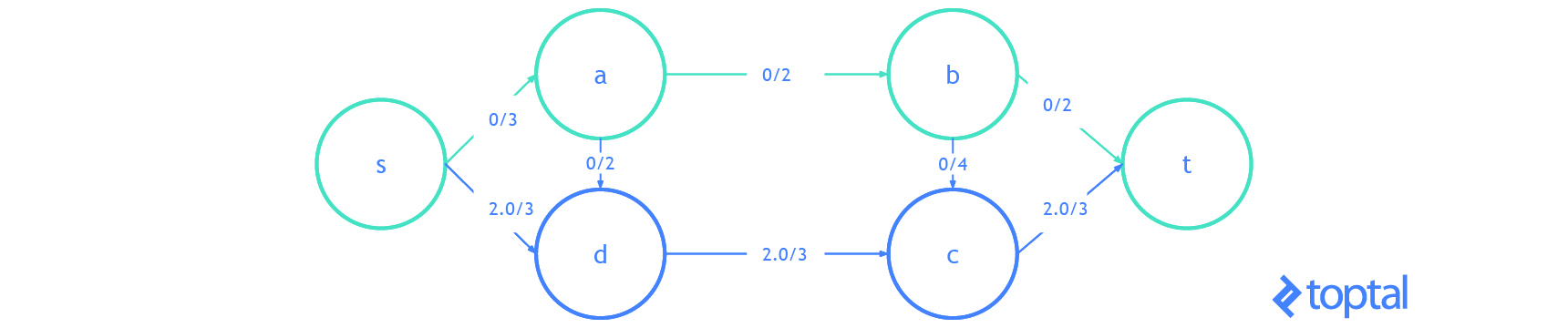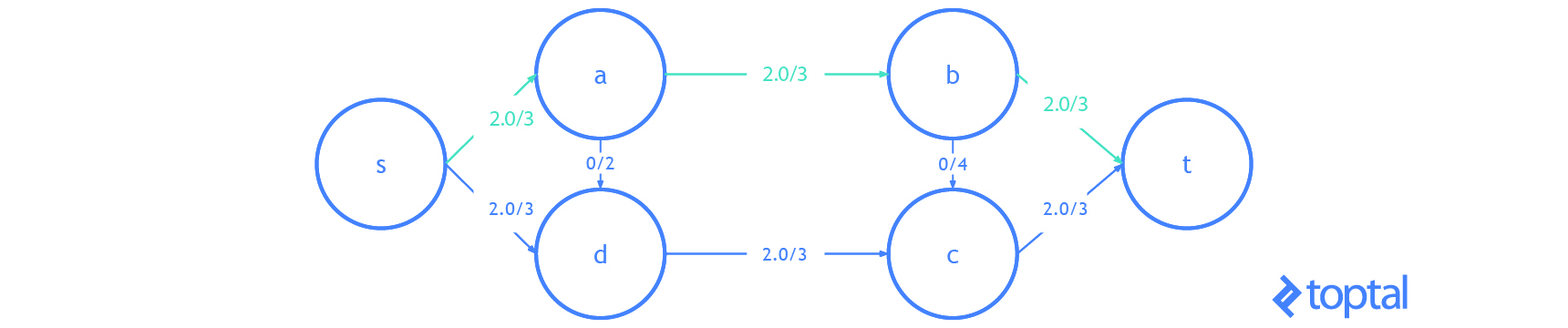
s-t Cut Flow
Let mfps represent a MaxFlowProblemState and let stCut represent a cut of mfps.G. The cut flow of stCut is defined:
def get_stcut_flow(stCut,mfps):
s = find_node_by_uid(mfps.sourceNodeUid, mfps.G)
t = find_node_by_uid(mfps.terminalNodeUid, mfps.G)
part_1 = get_first_part(stCut.cut,mfps.G)
part_2 = get_second_part(stCut.cut,mfps.G)
s_part = part_1 if s in part_1 else part_2
t_part = part_1 if t in part_1 else part_2
s_t_sum = sum(a.datum.flow for a in mfps.G.setOfArcs if (a in stCut.cut.setOfCutArcs) and (a.fromNode in s_part) )
t_s_sum = sum(a.datum.flow for a in mfps.G.setOfArcs if (a in stCut.cut.setOfCutArcs) and (a.fromNode in t_part) )
cut_flow = s_t_sum - t_s_sum
return cut_flow
s-t cut flow is the sum of flows from the partition containing the source node to the partition containing the terminal node minus the sum of flows from the partition containing the terminal node to the partition containing the source node.
Max Flow, Min Cut
Let maxFlowProblem represent a maximum flow problem and let the solution to maxFlowProblem be represented by a flow network represented as digraph H.
Let minStCut be the minimum capacity cut of the flow network represented by maxFlowProblem.G.
Because in the maximum flow problem flow originates in only a single source node and terminates at a single terminal node and, because of the capacity constraints and the conservation constraints, we know that the all of the flow entering maxFlowProblem.terminalNodeUid must cross any s-t cut, in particular it must cross minStCut. This means:
get_flow_value(H, maxFlowProblem) <= cut_capacity(minStCut, maxFlowProblem.G)
Solving the Maximum Flow Problem
The basic idea for solving a maximum flow problem maxFlowProblem is to start with a maximum flow solution represented by digraph H. Such a starting point can be H = strip_flows(maxFlowProblem.G). The task is then to use H and by some greedy modification of the a.datum.flow values of some arcs a in H.setOfArcs to produce another maximum flow solution represented by digraph K such that K cannot still represent a flow network with feasible flows and get_flow_value(H, maxFlowProblem) < get_flow_value(K, maxFlowProblem). As long as this process continues, the quality (get_flow_value(K, maxFlowProblem)) of the most recently encountered maximum flow solution (K) is better than any other maximum flow solution that has been found. If the process reaches a point that it knows that no other improvement is possible, the process can terminate and it will return the optimal maximum flow solution.
The description above is general and skips many proofs such as whether such a process is possible or how long it may take, I’ll give a few more details and the algorithm.
The Max Flow, Min Cut Theorem
From the book Flows in Networks by Ford and Fulkerson, the statement of the max flow, min cut theorem (Theorem 5.1) is:
For any network, the maximal flow value from
stotis equal to the minimum cut capacity of all cuts separatingsandt.
Using the definitions in this post, that translates to:
The solution to a maxFlowProblem represented by a flow network represented as digraph H is optimal if:
get_flow_value(H, maxFlowProblem) == cut_capacity(minStCut, maxFlowProblem.G)
I like this proof of the theorem and Wikipedia has another one.
The max flow, min cut theorem is used to prove the correctness and completeness of the Ford-Fulkerson method.
I’ll also give a proof of the theorem in the section after augmenting paths.
The Ford-Fulkerson Method and the Edmonds-Karp Algorithm
CLRS defines the Ford-Fulkerson method like so (section 26.2):
FORD-FULKERSON-METHOD(G, s, t):
initialize flow f to 0
while there exists an augmenting path p in the residual graph G_f augment flow f along
Residual Graph
The Residual Graph of a flow network represented as the digraph G can be represented as a digraph G_f:
ResidualDatum = namedtuple('ResidualDatum', ['residualCapacity','action'])
def agg_n_to_u_cap(n,u,G_as_dict):
arcs_out = G_as_dict[n]
return sum([a.datum.capacity for a in arcs_out if( (a.fromNode == n) and (a.toNode == u) ) ])
def agg_n_to_u_flow(n,u,G_as_dict):
arcs_out = G_as_dict[n]
return sum([a.datum.flow for a in arcs_out if( (a.fromNode == n) and (a.toNode == u) ) ])
def get_residual_graph_of(G):
G_as_dict = digraph_to_dict(G)
residual_nodes = G.setOfNodes
residual_arcs = frozenset([])
for n in G_as_dict:
arcs_from = G_as_dict[n]
nodes_to = frozenset([find_node_by_uid(a.toNode.uid,G) for a in arcs_from])
for u in nodes_to:
n_to_u_cap_sum = agg_n_to_u_cap(n,u,G_as_dict)
n_to_u_flow_sum = agg_n_to_u_flow(n,u,G_as_dict)
if(n_to_u_cap_sum > n_to_u_flow_sum):
flow = round(n_to_u_cap_sum - n_to_u_flow_sum, TOL)
residual_arcs = residual_arcs.union( frozenset([Arc(n,u,datum=ResidualDatum(flow, 'push'))]) )
if(n_to_u_flow_sum > 0.0):
flow = round(n_to_u_flow_sum, TOL)
residual_arcs = residual_arcs.union( frozenset([Arc(u,n,datum=ResidualDatum(flow, 'pull'))]) )
return DiGraph(residual_nodes, residual_arcs)
-
agg_n_to_u_cap(n,u,G_as_dict)returns the sum ofa.datum.capacityfor all arcs in the subset ofG.setOfArcswhere arcais in the subset ifa.fromNode = nanda.toNode = u. -
agg_n_to_u_cap(n,u,G_as_dict)returns the sum ofa.datum.flowfor all arcs in the subset ofG.setOfArcswhere arcais in the subset ifa.fromNode = nanda.toNode = u.
Briefly, the residual graph G_f represents certain actions which can be performed on the digraph G.
Each pair of nodes n,u in G.setOfNodes of the flow network represented by digraph G can generate 0, 1, or 2 arcs in the residual graph G_f of G.
-
The pair
n,udoes not generate any arcs inG_fif there is no arcainG.setOfArcssuch thata.fromNode = nanda.toNode = u. -
The pair
n,ugenerates the arcainG_f.setOfArcswherearepresents an arc labeled a push flow arc fromntoua = Arc(n,u,datum=ResidualNode(n_to_u_cap_sum - n_to_u_flow_sum))ifn_to_u_cap_sum > n_to_u_flow_sum. -
The pair
n,ugenerates the arcainG_f.setOfArcswherearepresents an arc labeled a pull flow arc fromntoua = Arc(n,u,datum=ResidualNode(n_to_u_cap_sum - n_to_u_flow_sum))ifn_to_u_flow_sum > 0.0.
-
Each push flow arc in
G_f.setOfArcsrepresents the action of adding a total ofx <= n_to_u_cap_sum - n_to_u_flow_sumflow to arcs in the subset ofG.setOfArcswhere arcais in the subset ifa.fromNode = nanda.toNode = u. -
Each pull flow arc in
G_f.setOfArcsrepresents the action of subtracting a total ofx <= n_to_u_flow_sumflow to arcs in the subset ofG.setOfArcswhere arcais in the subset ifa.fromNode = nanda.toNode = u.
Performing an individual push or pull action from G_f on the applicable arcs in G might generate a flow network without feasible flows because the capacity constraints or the conservation constraints might be violated in the generated flow network.
Here’s a visualization of the residual graph of the previous example visualization of a maximum flow solution, in the visualization each arc a represents a.residualCapacity.

Augmenting Path
Let maxFlowProblem be a max flow problem, and let G_f = get_residual_graph_of(G) be the residual graph of maxFlowProblem.G.
An augmenting path augmentingPath for maxFlowProblem is any path from find_node_by_uid(maxFlowProblem.sourceNode,G_f) to find_node_by_uid(maxFlowProblem.terminalNode,G_f).
It turns out that an augmenting path augmentingPath can be applied to a max flow solution represented by digraph H generating another max flow solution represented by digraph K where get_flow_value(H, maxFlowProblem) < get_flow_value(K, maxFlowProblem) if H is not optimal.
Here’s how:
def augment(augmentingPath, H):
augmentingPath = list(augmentingPath)
H_as_dict = digraph_to_dict(H)
new_nodes = frozenset({})
new_arcs = frozenset({})
visited_nodes = frozenset({})
visited_arcs = frozenset({})
bottleneck_residualCapacity = min( augmentingPath, key=lambda a: a.datum.residualCapacity ).datum.residualCapacity
for x in augmentingPath:
from_node_uid = x.fromNode.uid if x.datum.action == 'push' else x.toNode.uid
to_node_uid = x.toNode.uid if x.datum.action == 'push' else x.fromNode.uid
from_node = find_node_by_uid( from_node_uid, H )
to_node = find_node_by_uid( to_node_uid, H )
load = bottleneck_residualCapacity if x.datum.action == 'push' else -bottleneck_residualCapacity
for a in H_as_dict[from_node]:
if(a.toNode == to_node):
test_sum = a.datum.flow + load
new_flow = a.datum.flow
new_from_node_flow_out = a.fromNode.datum.flowOut
new_to_node_flow_in = a.toNode.datum.flowIn
new_from_look = {n for n in new_nodes if (n.uid == a.fromNode.uid)}
new_to_look = {n for n in new_nodes if (n.uid == a.toNode.uid) }
prev_from_node = new_from_look.pop() if (len(new_from_look)>0) else a.fromNode
prev_to_node = new_to_look.pop() if (len(new_to_look)>0) else a.toNode
new_nodes = new_nodes.difference(frozenset({prev_from_node}))
new_nodes = new_nodes.difference(frozenset({prev_to_node}))
if(test_sum > a.datum.capacity):
new_flow = a.datum.capacity
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow + a.datum.capacity
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow + a.datum.capacity
load = test_sum - a.datum.capacity
elif(test_sum < 0.0):
new_flow = 0.0
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow
load = test_sum
else:
new_flow = test_sum
new_from_node_flow_out = prev_from_node.datum.flowOut - a.datum.flow + new_flow
new_to_node_flow_in = prev_to_node.datum.flowIn - a.datum.flow + new_flow
load = 0.0
new_from_node_flow_out = round(new_from_node_flow_out, TOL)
new_to_node_flow_in = round(new_to_node_flow_in, TOL)
new_flow = round(new_flow, TOL)
new_from_node = Node(prev_from_node.uid, FlowNodeDatum(prev_from_node.datum.flowIn, new_from_node_flow_out))
new_to_node = Node(prev_to_node.uid, FlowNodeDatum(new_to_node_flow_in, prev_to_node.datum.flowOut))
new_arc = Arc(new_from_node, new_to_node, FlowArcDatum(a.datum.capacity, new_flow))
visited_nodes = visited_nodes.union(frozenset({a.fromNode,a.toNode}))
visited_arcs = visited_arcs.union(frozenset({a}))
new_nodes = new_nodes.union(frozenset({new_from_node, new_to_node}))
new_arcs = new_arcs.union(frozenset({new_arc}))
not_visited_nodes = H.setOfNodes.difference(visited_nodes)
not_visited_arcs = H.setOfArcs.difference(visited_arcs)
full_new_nodes = new_nodes.union(not_visited_nodes)
full_new_arcs = new_arcs.union(not_visited_arcs)
G = DiGraph(full_new_nodes, full_new_arcs)
full_new_arcs_update = frozenset([])
for a in full_new_arcs:
new_from_node = a.fromNode
new_to_node = a.toNode
new_from_node = find_node_by_uid( a.fromNode.uid, G )
new_to_node = find_node_by_uid( a.toNode.uid, G )
full_new_arcs_update = full_new_arcs_update.union( {Arc(new_from_node, new_to_node, FlowArcDatum(a.datum.capacity, a.datum.flow))} )
G = DiGraph(full_new_nodes, full_new_arcs_update)
return G
In the above, TOL is some tolerance value for rounding the flow values in the network. This is to avoid cascading imprecision of floating point calculations. So, for example, I used TOL = 10 to mean round to 10 significant digits.
Let K = augment(augmentingPath, H), then K represents a feasible max flow solution for maxFlowProblem. For the statement to be true, the flow network represented by K must have feasible flows (not violate the capacity constraint or the conservation constraint.
Here’s why: In the method above, each node added to the new flow network represented by digraph K is either an exact copy of a node from digraph H or a node n which has had the same number added to its n.datum.flowIn as its n.datum.flowOut. This means that the conservation constraint is satisfied in K as long as it was satisfied in H. The conservation constraint is satisfied because we explicitly check that any new arc a in the network has a.datum.flow <= a.datum.capacity; thus, as long as the arcs from the set H.setOfArcs which were copied unmodified into K.setOfArcs do not violate the capacity constraint, then K does not violate the capacity constraint.
It’s also true that get_flow_value(H, maxFlowProblem) < get_flow_value(K, maxFlowProblem) if H is not optimal.
Here’s why: For an augmenting path augmentingPath to exist in the digraph representation of the residual graph G_f of a max flow problem maxFlowProblem then the last arc a on augmentingPath must be a ‘push’ arc and it must have a.toNode == maxFlowProblem.terminalNode. An augmenting path is defined as one which terminates at the terminal node of the max flow problem for which it is an augmenting path. From the definition of the residual graph, it is clear that the last arc in an augmenting path on that residual graph must be a ‘push’ arc because any ‘pull’ arc b in the augmenting path will have b.toNode == maxFlowProblem.terminalNode and b.fromNode != maxFlowProblem.terminalNode from the definition of path. Additionally, from the definition of path, it is clear that the terminal node is only modified once by the augment method. Thus augment modifies maxFlowProblem.terminalNode.flowIn exactly once and it increases the value of maxFlowProblem.terminalNode.flowIn because the last arc in the augmentingPath must be the arc which causes the modification in maxFlowProblem.terminalNode.flowIn during augment. From the definition of augment as it applies to ‘push’ arcs, the maxFlowProblem.terminalNode.flowIn can only be increased, not decreased.
Some Proofs from Sedgewick and Wayne
The book Algorithms, fourth edition by Robert Sedgewich and Kevin Wayne has some wonderful and short proofs (pages 892-894) that will be useful. I’ll recreate them here, though I’ll use language fitting in with previous definitions. My labels for the proofs are the same as in the Sedgewick book.
Proposition E: For any digraph H representing a feasible maximum flow solution to a maximum flow problem maxFlowProblem, for any stCut get_stcut_flow(stCut,H,maxFlowProblem) = get_flow_value(H, maxFlowProblem).
Proof: Let stCut=stCut(maxFlowProblem.sourceNode,maxFlowProblem.terminalNode,set([a for a in H.setOfArcs if a.toNode == maxFlowProblem.terminalNode])). Proposition E holds for stCut directly from the definition of s-t flow value. Suppose that there we wish to move some node n from the s-partition (get_first_part(stCut.cut, G)) and into the t-partition (get_second_part(stCut.cut, G)), to do so we need to change stCut.cut, which could change stcut_flow = get_stcut_flow(stCut,H,maxFlowProblem) and invalidate proposition E. However, let’s see how the value of stcut_flow will change as we make this change. node n is at equilibrium meaning that the sum of flow into node n is equal to the sum of flow out of it (this is necessary for H to represent a feasible solution). Notice that all flow which is part of the stcut_flow entering node n enters it from the s-partition (flow entering node n from the t-partition either directly or indirectly would not have been counted in the stcut_flow value because it is heading the wrong direction based on the definition). Additionally, all flow exiting n will eventually (directly or indirectly) flow into the terminal node (proved earlier). When we move node n into the t-partition, all the flow entering n from the s-partition must be added to the new stcut_flow value; however, all flow exiting n must the be subtracted from the new stcut_flow value; the part of the flow heading directly into the t-partition is subtracted because this flow is now internal to the new t-partition and is not counted as stcut_flow. The part of the flow from n heading into nodes in the s-partition must also be subtracted from stcut_flow: After n is moved into the t-partition, these flows will be directed from the t-partition and into the s-partition and so must not be accounted for in the stcut_flow, since these flows are removed the inflow into the s-partition and must be reduced by the sum of these flows, and the outflow from the s-partition into the t-partition (where all flows from s-t must end up) must be reduced by the same amount. As node n was at equilibrium prior to the process, the update will have added the same value to the new stcut_flow value as it subtracted thus leaving proposition E true after the update. The validity of proposition E then follows from induction on the size of the t-partition.
Here are some example flow networks to help visualize the less obvious cases where proposition E holds; in the image, the red areas indicate the s-partition, the blue areas represent the t-partition, and the green arcs indicate an s-t cut. In the second image, flow between node A and node B increases while the flow into terminal node t doesn’t change.:
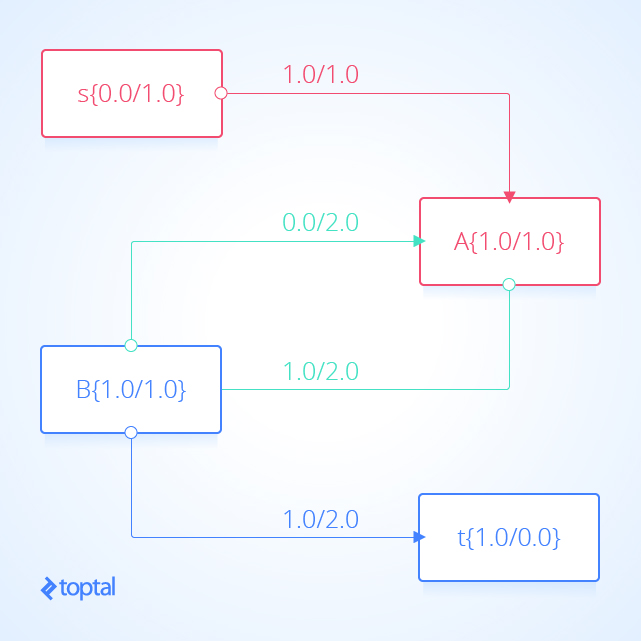
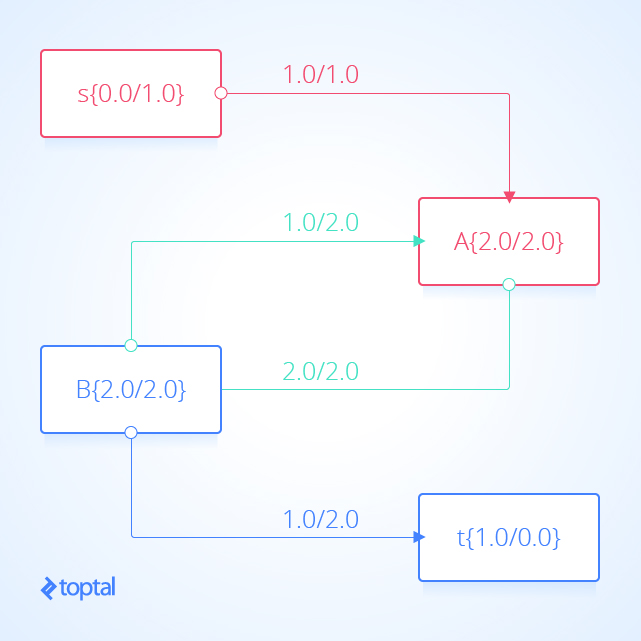
Corollary: No s-t cut flow value can exceed the capacity of any s-t cut.
Proposition F. (max flow, min cut theorem): Let f be an s-t flow. The following 3 conditions are equivalent:
-
There exists an s-t cut whose capacity equals the value of the flow
f. -
fis a max flow. -
There is no augmenting path with respect to
f.
Condition 1 implies condition 2 by the corollary. Condition 2 implies condition 3 because the existence of an augmenting path implies the existence of a flow with larger values, contradicting the maximality of f. Condition 3 implies condition 1: Let C_s be the set of all nodes that can be reached from s with an augmenting path in the residual graph. Let C_t be the remaining arcs, then t must be in C_t (by our assumption). The arcs crossing from C_s to C_t then form an s-t cut which contains only arcs a where either a.datum.capacity = a.datum.flow or a.datum.flow = 0.0. If this were otherwise then the nodes connected by an arc with remaining residual capacity to C_s would be in the set C_s since there would then be an augmenting path from s to such a node. The flow across the s-t cut is equal to the s-t cut’s capacity (since arcs from C_s to C_t have flow equal to capacity) and also to the value of the s-t flow (by proposition E).
This statement of the max flow, min cut theorem implies the earlier statement from Flows in Networks.
Corollary (integrality property): When capacities are integers, there exists an integer-valued max flow, and the Ford-Fulkerson algorithm finds it.
Proof: Each augmenting path increases the flow by a positive integer, the minimum of the unused capacities in the ‘push’ arcs and the flows in the ‘pull’ arcs, all of which are always positive integers.
This justifies the Ford-Fulkerson method description from CLRS. The method is to keep finding augmenting paths and applying augment to the latest maxFlowSolution coming up with better solutions, until no more augmenting path meaning that the latest maximum flow solution is optimal.
From Ford-Fulkerson to Edmonds-Karp
The remaining questions regarding solving maximum flow problems are:
-
How should augmenting paths be constructed?
-
Will the method terminate if we use real numbers and not integers?
-
How long will it take to terminate (if it does)?
The Edmonds-Karp algorithm specifies that each augmenting path is constructed by a breadth first search (BFS) of the residual graph; it turns out that this decision of point 1 above will also force the algorithm to terminate (point 2) and allows the asymptotic time and space complexity to be determined.
First, here’s a BFS implementation:
def bfs(sourceNode, terminalNode, G_f):
G_f_as_dict = digraph_to_dict(G_f)
parent_arcs = dict([])
visited = frozenset([])
deq = deque([sourceNode])
while len(deq) > 0:
curr = deq.popleft()
if curr == terminalNode:
break
for a in G_f_as_dict.get(curr):
if (a.toNode not in visited):
visited = visited.union(frozenset([a.toNode]))
parent_arcs[a.toNode] = a
deq.extend([a.toNode])
path = list([])
curr = terminalNode
while(curr != sourceNode):
if (curr not in parent_arcs):
err_msg = 'No augmenting path from {} to {}.'.format(sourceNode.uid, terminalNode.uid)
raise StopIteration(err_msg)
path.extend([parent_arcs[curr]])
curr = parent_arcs[curr].fromNode
path.reverse()
test = deque([path[0].fromNode])
for a in path:
if(test[-1] != a.fromNode):
err_msg = 'Bad path: {}'.format(path)
raise ValueError(err_msg)
test.extend([a.toNode])
return path
I used a deque from the python collections module.
To answer question 2 above, I’ll paraphrase another proof from Sedgewick and Wayne: Proposition G. The number of augmenting paths needed in the Edmonds-Karp algorithm with N nodes and A arcs is at most NA/2. Proof: Every augmenting path has a bottleneck arc- an arc that is deleted from the residual graph because it corresponds either to a ‘push’ arc that becomes filled to capacity or a ‘pull’ arc through which the flow becomes 0. Each time an arc becomes a bottleneck arc, the length of any augmenting path through it must increase by a factor of 2. This is because each node in a path may appear only once or not at all (from the definition of path) since the paths are being explored from shortest path to longest that means that at least one more node must be visited by the next path that goes through the particular bottleneck node that means an additional 2 arcs on the path before we arrive at the node. Since the augmenting path is of length at most N each arc can be on at most N/2 augmenting paths, and the total number of augmenting paths is at most NA/2.
The Edmonds-Karp algorithm executes in O(NA^2). If at most NA/2 paths will be explored during the algorithm and exploring each path with BFS is N+A then the most significant term of the product and hence the asymptotic complexity is O(NA^2).
Let mfp be a maxFlowProblemState.
def edmonds_karp(mfp):
sid, tid = mfp.sourceNodeUid, mfp.terminalNodeUid
no_more_paths = False
loop_count = 0
while(not no_more_paths):
residual_digraph = get_residual_graph_of(mfp.G)
try:
asource = find_node_by_uid(mfp.sourceNodeUid, residual_digraph)
aterm = find_node_by_uid(mfp.terminalNodeUid, residual_digraph)
apath = bfs(asource, aterm, residual_digraph)
paint_mfp_path(mfp, loop_count, apath)
G = augment(apath, mfp.G)
s = find_node_by_uid(sid, G)
t = find_node_by_uid(tid, G)
mfp = MaxFlowProblemState(G, s.uid, t.uid, mfp.maxFlowProblemStateUid)
loop_count += 1
except StopIteration as e:
no_more_paths = True
return mfp
The version above is inefficient and has worse complexity than O(NA^2) since it constructs a new maximum flow solution and new a residual graph each time (rather than modifying existing digraphs as the algorithm advances). To get to a true O(NA^2) solution the algorithm must maintain both the digraph representing the maximum flow problem state and its associated residual graph. So the algorithm must avoid iterating over arcs and nodes unnecessarily and update their values and associated values in the residual graph only as necessary.
To write a faster Edmonds Karp algorithm, I rewrote several pieces of code from the above. I hope that going through the code which generated a new digraph was helpful in understanding what’s going on. In the fast algorithm, I use some new tricks and Python data structures that I don’t want to go over in detail. I will say that a.fromNode and a.toNode are now treated as strings and uids to nodes. For this code, let mfps be a maxFlowProblemState
import uuid
def fast_get_mfps_flow(mfps):
flow_from_s = {n for n in mfps.G.setOfNodes if n.uid == mfps.sourceNodeUid}.pop().datum.flowOut
flow_to_t = {n for n in mfps.G.setOfNodes if n.uid == mfps.terminalNodeUid}.pop().datum.flowIn
if( (flow_to_t - flow_from_s) > 0.00):
raise Exception('Infeasible s-t flow')
return flow_to_t
def fast_e_k_preprocess(G):
G = strip_flows(G)
get = dict({})
get['nodes'] = dict({})
get['node_to_node_capacity'] = dict({})
get['node_to_node_flow'] = dict({})
get['arcs'] = dict({})
get['residual_arcs'] = dict({})
for a in G.setOfArcs:
if(a.fromNode not in G.setOfNodes):
err_msg = 'There is no Node {a.fromNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
if(a.toNode not in G.setOfNodes):
err_msg = 'There is no Node {a.toNode.uid!s} to match the Arc from {a.fromNode.uid!s} to {a.toNode.uid!s}'.format(**locals())
raise KeyError(err_msg)
get['nodes'][a.fromNode.uid] = a.fromNode
get['nodes'][a.toNode.uid] = a.toNode
lark = Arc(a.fromNode.uid, a.toNode.uid, FlowArcDatumWithUid(a.datum.capacity, a.datum.flow, uuid.uuid4()))
if(a.fromNode.uid not in get['arcs']):
get['arcs'][a.fromNode.uid] = dict({a.toNode.uid : dict({lark.datum.uid : lark})})
else:
if(a.toNode.uid not in get['arcs'][a.fromNode.uid]):
get['arcs'][a.fromNode.uid][a.toNode.uid] = dict({lark.datum.uid : lark})
else:
get['arcs'][a.fromNode.uid][a.toNode.uid][lark.datum.uid] = lark
for a in G.setOfArcs:
if a.toNode.uid not in get['arcs']:
get['arcs'][a.toNode.uid] = dict({})
for n in get['nodes']:
get['residual_arcs'][n] = dict()
get['node_to_node_capacity'][n] = dict()
get['node_to_node_flow'][n] = dict()
for u in get['nodes']:
n_to_u_cap_sum = sum(a.datum.capacity for a in G.setOfArcs if (a.fromNode.uid == n) and (a.toNode.uid == u) )
n_to_u_flow_sum = sum(a.datum.flow for a in G.setOfArcs if (a.fromNode.uid == n) and (a.toNode.uid == u) )
if(n_to_u_cap_sum > n_to_u_flow_sum):
flow = round(n_to_u_cap_sum - n_to_u_flow_sum, TOL)
get['residual_arcs'][n][u] = Arc(n,u,ResidualDatum(flow, 'push'))
if(n_to_u_flow_sum > 0.0):
flow = round(n_to_u_flow_sum, TOL)
get['residual_arcs'][u][n] = Arc(u,n,ResidualDatum(flow, 'pull'))
get['node_to_node_capacity'][n][u] = n_to_u_cap_sum
get['node_to_node_flow'][n][u] = n_to_u_flow_sum
return get
def fast_bfs(sid, tid, get):
parent_of = dict([])
visited = frozenset([])
deq = coll.deque([sid])
while len(deq) > 0:
n = deq.popleft()
if n == tid:
break
for u in get['residual_arcs'][n]:
if (u not in visited):
visited = visited.union(frozenset({u}))
parent_of[u] = get['residual_arcs'][n][u]
deq.extend([u])
path = list([])
curr = tid
while(curr != sid):
if (curr not in parent_of):
err_msg = 'No augmenting path from {} to {}.'.format(sid, curr)
raise StopIteration(err_msg)
path.extend([parent_of[curr]])
curr = parent_of[curr].fromNode
path.reverse()
return path
def fast_edmonds_karp(mfps):
sid, tid = mfps.sourceNodeUid, mfps.terminalNodeUid
get = fast_e_k_preprocess(mfps.G)
no_more_paths, loop_count = False, 0
while(not no_more_paths):
try:
apath = fast_bfs(sid, tid, get)
get = fast_augment(apath, get)
loop_count += 1
except StopIteration as e:
no_more_paths = True
nodes = frozenset(get['nodes'].values())
arcs = frozenset({})
for from_node in get['arcs']:
for to_node in get['arcs'][from_node]:
for arc in get['arcs'][from_node][to_node]:
arcs |= frozenset({get['arcs'][from_node][to_node][arc]})
G = DiGraph(nodes, arcs)
mfps = MaxFlowProblemState(G, sourceNodeUid=sid, terminalNodeUid=tid, maxFlowProblemStateUid=mfps.maxFlowProblemStateUid)
return mfps
Here’s a visualization of how this algorithm solves the example flow network from above. The visualization shows the steps as they are reflected in the digraph G representing the most up-to-date flow network and as they are reflected in the residual graph of that flow network. Augmenting paths in the residual graph are shown as red paths, and the digraph representing the problem the set of nodes and arcs affected by a given augmenting path is highlighted in green. In each case, I’ll highlight the parts of the graph that will be changed (in red or green) and then show the graph after the changes (just in black).


Here’s another visualization of how this algorithm solving a different example flow network. Notice that this one uses real numbers and contains multiple arcs with the same fromNode and toNode values.
**Also notice that because Arcs with a ‘pull’ ResidualDatum may be part of the Augmenting Path, the nodes affected in the DiGraph of the Flown Network _may not be on a path in G!.
Bipartite Graphs
Suppose we have a digraph G, G is bipartite if it’s possible to partition the nodes in G.setOfNodes into two sets (part_1 and part_2) such that for any arc a in G.setOfArcs it cannot be true that a.fromNode in part_1 and a.toNode in part_1. It also cannot be true that a.fromNode in part_2 and a.toNode in part_2.
In other words G is bipartite if it can be partitioned into two sets of nodes such that every arc must connect a node in one set to a node in the other set.
Testing Bipartite
Suppose we have a digraph G, we want to test if it is bipartite. We can do this in O(|G.setOfNodes|+|G.setOfArcs|) by greedy coloring the graph into two colors.
First, we need to generate a new digraph H. This graph will have will have the same set of nodes as G, but it will have more arcs than G. Every arc a in G will create 2 arcs in H; the first arc will be identical to a, and the second arc reverses the director of a ( b = Arc(a.toNode,a.fromNode,a.datum)).
Bipartition = coll.namedtuple('Bipartition',['firstPart', 'secondPart', 'G'])
def bipartition(G):
nodes = frozenset(G.setOfNodes
arcs = frozenset(G.setOfArcs)
arcs = arcs.union( frozenset( {Arc(a.toNode,a.fromNode,a.datum) for a in G.setOfArcs} ) )
H = DiGraph(nodes, arcs)
H_as_dict = digraph_to_dict(H)
color = dict([])
some_node = next(iter(H.setOfNodes))
deq = coll.deque([some_node])
color[some_node] = -1
while len(deq) > 0:
curr = deq.popleft()
for a in H_as_dict.get(curr):
if (a.toNode not in color):
color[a.toNode] = -1*color[curr]
deq.extend([a.toNode])
elif(color[curr] == color[a.toNode]):
print(curr,a.toNode)
raise Exception('Not Bipartite.')
firstPart = frozenset( {n for n in color if color[n] == -1 } )
secondPart = frozenset( {n for n in color if color[n] == 1 } )
if( firstPart.union(secondPart) != G.setOfNodes ):
raise Exception('Not Bipartite.')
return Bipartition(firstPart, secondPart, G)
Matchings and Maximum Matchings
Suppose we have a digraph G and matching is a subset of arcs from G.setOfArcs. matching is a matching if for any two arcs a and b in matching: len(frozenset( {a.fromNode} ).union( {a.toNode} ).union( {b.fromNode} ).union( {b.toNode} )) == 4. In other words, no two arcs in a matching share a node.
Matching matching, is a maximum matching if there is no other matching alt_matching in G such that len(matching) < len(alt_matching). In other words, matching is a maximum matching if it is the largest set of arcs from G.setOfArcs that still satisfies the definition of matching (the addition of any arc not already in the matching will break the matching definition).
A maximum matching matching is a perfect matching if every for node n in G.setOfArcs there exists an arc a in matching where a.fromNode == n or a.toNode == n.
Maximum Bipartite Matching
A maximum bipartite matching is a maximum matching on a digraph G which is bipartite.
Given that G is bipartite, the problem of finding a maximum bipartite matching can be transformed into a maximum flow problem solvable with the Edmonds-Karp algorithm and then the maximum bipartite matching can be recovered from the solution to the maximum flow problem.
Let bipartition be a bipartition of G.
To do this, I need to generate a new digraph (H) with some new nodes (H.setOfNodes) and some new arcs (H.setOfArcs). H.setOfNodes contains all the nodes in G.setOfNodes and two more nodess, s (a source node) and t (a terminal node).
H.setOfArcs will contain one arc for each G.setOfArcs. If an arc a is in G.setOfArcs and a.fromNode is in bipartition.firstPart and a.toNode is in bipartition.secondPart then include a in H (adding a FlowArcDatum(1,0)).
If a.fromNode is in bipartition.secondPart and a.toNode is in bipartition.firstPart, then include Arc(a.toNode,a.fromNode,FlowArcDatum(1,0)) in H.setOfArcs.
The definition of a bipartite graph ensures that no arc connects any nodes where both nodes are in the same partition. H.setOfArcs also contains an arc from node s to each node in bipartition.firstPart. Finally, H.setOfArcs contains an arc each node in bipartition.secondPart to node t. a.datum.capacity = 1 for all a in H.setOfArcs.
First partition the nodes in G.setOfNodes the two disjoint sets (part1 and part2) such that no arc in G.setOfArcs is directed from one set to the same set (this partition is possible because G is bipartite). Next, add all arcs in G.setOfArcs which are directed from part1 to part2 into H.setOfArcs. Then create a single source node s and a single terminal node t and create some more arcs
Then, construct a maxFlowProblemState.
def solve_mbm( bipartition ):
s = Node(uuid.uuid4(), FlowNodeDatum(0,0))
t = Node(uuid.uuid4(), FlowNodeDatum(0,0))
translate = {}
arcs = frozenset([])
for a in bipartition.G.setOfArcs:
if ( (a.fromNode in bipartition.firstPart) and (a.toNode in bipartition.secondPart) ):
fark = Arc(a.fromNode,a.toNode,FlowArcDatum(1,0))
arcs = arcs.union({fark})
translate[frozenset({a.fromNode.uid,a.toNode.uid})] = a
elif ( (a.toNode in bipartition.firstPart) and (a.fromNode in bipartition.secondPart) ):
bark = Arc(a.toNode,a.fromNode,FlowArcDatum(1,0))
arcs = arcs.union({bark})
translate[frozenset({a.fromNode.uid,a.toNode.uid})] = a
arcs1 = frozenset( {Arc(s,n,FlowArcDatum(1,0)) for n in bipartition.firstPart } )
arcs2 = frozenset( {Arc(n,t,FlowArcDatum(1,0)) for n in bipartition.secondPart } )
arcs = arcs.union(arcs1.union(arcs2))
nodes = frozenset( {Node(n.uid,FlowNodeDatum(0,0)) for n in bipartition.G.setOfNodes} ).union({s}).union({t})
G = DiGraph(nodes, arcs)
mfp = MaxFlowProblemState(G, s.uid, t.uid, 'bipartite')
result = edmonds_karp(mfp)
lookup_set = {a for a in result.G.setOfArcs if (a.datum.flow > 0) and (a.fromNode.uid != s.uid) and (a.toNode.uid != t.uid)}
matching = {translate[frozenset({a.fromNode.uid,a.toNode.uid})] for a in lookup_set}
return matching
Minimal Node Cover
A node cover in a digraph G is a set of nodes (cover) from G.setOfNodes such that for any arc a of G.setOfArcs this must be true: (a.fromNode in cover) or (a.toNode in cover).
A minimal node cover is the smallest possible set of nodes in the graph that is still a node cover. König’s theorem states that in a bipartite graph, the size of the maximum matching on that graph is equal to the size of the minimal node cover, and it suggests how the node cover can recovered from a maximum matching:
Suppose we have the bipartition bipartition and the maximum matching matching. Define a new digraph H, H.setOfNodes=G.setOfNodes, the arcs in H.setOfArcs are the union of two sets.
The first set is arcs a in matching, with the change that if a.fromNode in bipartition.firstPart and a.toNode in bipartition.secondPart then a.fromNode and a.toNode are swapped in the created arc give such arcs a a.datum.inMatching=True attribute to indicate that they were derived from arcs in a matching.
The second set is arcs a NOT in matching, with the change that if a.fromNode in bipartition.secondPart and a.toNode in bipartition.firstPart then a.fromNode and a.toNode are swapped in the created arc (give such arcs a a.datum.inMatching=False attribute).
Next, run a depth first search (DFS) starting from each node n in bipartition.firstPart which is neither n == a.fromNode nor n == a.toNodes for any arc a in matching. During the DFS, some nodes are visited and some are not (store this information in a n.datum.visited field). The minimum node cover is the union of the nodes {a.fromNode for a in H.setOfArcs if ( (a.datum.inMatching) and (a.fromNode.datum.visited) ) } and the nodes {a.fromNode for a in H.setOfArcs if (a.datum.inMatching) and (not a.toNode.datum.visited)}.
This can be shown to lead from a maximum matching to a minimal node cover by a proof by contradiction, take some arc a that was supposedly not covered and consider all four cases regarding whether a.fromNode and a.toNode belong (whether as toNode or fromNode) to any arc in matching matching. Each case leads to a contradiction due to the order that DFS visits nodes and the fact that matching is a maximum matching.
Suppose we have a function to execute these steps and return the set of nodes comprising the minimal node cover when given the digraph G, and the maximum matching matching:
ArcMatchingDatum = coll.namedtuple('ArcMatchingDatum', ['inMatching' ])
NodeMatchingDatum = coll.namedtuple('NodeMatchingDatum', ['visited'])
def dfs_helper(snodes, G):
sniter, do_stop = iter(snodes), False
visited, visited_uids = set(), set()
while(not do_stop):
try:
stack = [ next(sniter) ]
while len(stack) > 0:
curr = stack.pop()
if curr.uid not in visited_uids:
visited = visited.union( frozenset( {Node(curr.uid, NodeMatchingDatum(False))} ) )
visited_uids = visited.union(frozenset({curr.uid}))
succ = frozenset({a.toNode for a in G.setOfArcs if a.fromNode == curr})
stack.extend( succ.difference( frozenset(visited) ) )
except StopIteration as e:
stack, do_stop = [], True
return visited
def get_min_node_cover(matching, bipartition):
nodes = frozenset( { Node(n.uid, NodeMatchingDatum(False)) for n in bipartition.G.setOfNodes} )
G = DiGraph(nodes, None)
charcs = frozenset( {a for a in matching if ( (a.fromNode in bipartition.firstPart) and (a.toNode in bipartition.secondPart) )} )
arcs0 = frozenset( { Arc(find_node_by_uid(a.toNode.uid,G), find_node_by_uid(a.fromNode.uid,G), ArcMatchingDatum(True) ) for a in charcs } )
arcs1 = frozenset( { Arc(find_node_by_uid(a.fromNode.uid,G), find_node_by_uid(a.toNode.uid,G), ArcMatchingDatum(True) ) for a in matching.difference(charcs) } )
not_matching = bipartition.G.setOfArcs.difference( matching )
charcs = frozenset( {a for a in not_matching if ( (a.fromNode in bipartition.secondPart) and (a.toNode in bipartition.firstPart) )} )
arcs2 = frozenset( { Arc(find_node_by_uid(a.toNode.uid,G), find_node_by_uid(a.fromNode.uid,G), ArcMatchingDatum(False) ) for a in charcs } )
arcs3 = frozenset( { Arc(find_node_by_uid(a.fromNode.uid,G), find_node_by_uid(a.toNode.uid,G), ArcMatchingDatum(False) ) for a in not_matching.difference(charcs) } )
arcs = arcs0.union(arcs1.union(arcs2.union(arcs3)))
G = DiGraph(nodes, arcs)
bip = Bipartition({find_node_by_uid(n.uid,G) for n in bipartition.firstPart},{find_node_by_uid(n.uid,G) for n in bipartition.secondPart},G)
match_from_nodes = frozenset({find_node_by_uid(a.fromNode.uid,G) for a in matching})
match_to_nodes = frozenset({find_node_by_uid(a.toNode.uid,G) for a in matching})
snodes = bip.firstPart.difference(match_from_nodes).difference(match_to_nodes)
visited_nodes = dfs_helper(snodes, bip.G)
not_visited_nodes = bip.G.setOfNodes.difference(visited_nodes)
H = DiGraph(visited_nodes.union(not_visited_nodes), arcs)
cover1 = frozenset( {a.fromNode for a in H.setOfArcs if ( (a.datum.inMatching) and (a.fromNode.datum.visited) ) } )
cover2 = frozenset( {a.fromNode for a in H.setOfArcs if ( (a.datum.inMatching) and (not a.toNode.datum.visited) ) } )
min_cover_nodes = cover1.union(cover2)
true_min_cover_nodes = frozenset({find_node_by_uid(n.uid, bipartition.G) for n in min_cover_nodes})
return min_cover_nodes
The Linear Assignment Problem
The linear assignment problem consists of finding a maximum weight matching in a weighted bipartite graph.
Problems like the one at the very start of this post can be expressed as a linear assignment problem. Given a set of workers, a set of tasks, and a function indicating the profitability of an assignment of one worker to one task, we want to maximize the sum of all assignments that we make; this is a linear assignment problem.
Assume that the number of tasks and workers are equal, though I will show that this assumption is easy to remove. In the implementation, I represent arc weights with an attribute a.datum.weight for an arc a.
WeightArcDatum = namedtuple('WeightArcDatum', [weight])
Kuhn-Munkres Algorithm
The Kuhn-Munkres Algorithm solves the linear assignment problem. A good implementation can take O(N^{4}) time, (where N is the number of nodes in the digraph representing the problem). An implementation that is easier to explain takes O(N^{5}) (for a version which regenerates DiGraphs) and O(N^{4}) for (for a version which maintains DiGraphs). This is similar to the two different implementations of the Edmonds-Karp algorithm.
For this description, I’m only working with complete bipartite graphs (those where half the nodes are in one part of the bipartition and the other half in the second part). In the worker, task motivation this means that there are as many workers as tasks.
This seems like a significant condition (what if these sets are not equal!) but it is easy to fix this issue; I talk about how to do that in the last section.
The version of the algorithm described here uses the useful concept of zero weight arcs. Unfortunately, this concept only makes sense when we are solving a minimization (if rather than maximizing the profits of our worker-task assignments we were instead minimizing the cost of such assignments).
Fortunately, it is easy to turn a maximum linear assignment problem into a minimum linear assignment problem by setting each the arc a weights to M-a.datum.weight where M=max({a.datum.weight for a in G.setOfArcs}). The solution to the original maximizing problem will be identical to the solution minimizing problem after the arc weights are changed. So for the remainder, assume that we make this change.
The Kuhn-Munkres algorithm solves minimum weight matching in a weighted bipartite graph by a sequence of maximum matchings in unweighted bipartite graphs. If a we find a perfect matching on the digraph representation of the linear assignment problem, and if the weight of every arc in the matching is zero, then we have found the minimum weight matching since this matching suggests that all nodes in the digraph have been matched by an arc with the lowest possible cost (no cost can be lower than 0, based on prior definitions).
No other arcs can be added to the matching (because all nodes are already matched) and no arcs should be removed from the matching because any possible replacement arc will have at least as great a weight value.
If we find a maximum matching of the subgraph of G which contains only zero weight arcs, and it is not a perfect matching, we don’t have a full solution (since the matching is not perfect). However, we can produce a new digraph H by changing the weights of arcs in G.setOfArcs in a way that new 0-weight arcs appear and the optimal solution of H is the same as the optimal solution of G. Since we guarantee that at least one zero weight arc is produced at each iteration, we guarantee that we will arrive at a perfect matching in no more than |G.setOfNodes|^{2}=N^{2} such iterations.
Suppose that in bipartition bipartition, bipartition.firstPart contains nodes representing workers, and bipartition.secondPart represents nodes representing tasks.
The algorithm starts by generating a new digraph H. H.setOfNodes = G.setOfNodes. Some arcs in H are generated from nodes n in bipartition.firstPart. Each such node n generates an arc b in H.setOfArcs for each arc a in bipartition.G.setOfArcs where a.fromNode = n or a.toNode = n, b=Arc(a.fromNode, a.toNode, a.datum.weight - z) where z=min(x.datum.weight for x in G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )).
More arcs in H are generated from nodes n in bipartition.secondPart. Each such node n generates an arc b in H.setOfArcs for each arc a in bipartition.G.setOfArcs where a.fromNode = n or a.toNode = n, b=Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) where z=min(x.datum.weight for x in G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )).
KMA: Next, form a new digraph K composed of only the zero weight arcs from H, and the nodes incident on those arcs. Form a bipartition on the nodes in K, then use solve_mbm( bipartition ) to get a maximum matching (matching) on K. If matching is a perfect matching in H (the arcs in matching are incident on all nodes in H.setOfNodes) then the matching is an optimal solution to the linear assignment problem.
Otherwise, if matching is not perfect, generate the minimal node cover of K using node_cover = get_min_node_cover(matching, bipartition(K)). Next, define z=min({a.datum.weight for a in H.setOfArcs if a not in node_cover}). Define nodes = H.setOfNodes, arcs1 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh-z)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) and (a.toNode not in node_cover)}, arcs2 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) != (a.toNode not in node_cover)}, arcs3 = {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh+z)) for a in H.setOfArcs if ( (a.fromNode in node_cover) and (a.toNode in node_cover)}. The != symbol in the previous expression acts as an XOR operator. Then arcs = arcs1.union(arcs2.union(arcs3)). Next, H=DiGraph(nodes,arcs). Go back to the label KMA. The algorithm continues until a perfect matching is produced. This matching is also the solution to the linear assignment problem.
def kuhn_munkres( bipartition ):
nodes = bipartition.G.setOfNodes
arcs = frozenset({})
for n in bipartition.firstPart:
z = min( {x.datum.weight for x in bipartition.G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )} )
arcs = arcs.union( frozenset({Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) }) )
for n in bipartition.secondPart:
z = min( {x.datum.weight for x in bipartition.G.setOfArcs if ( (x.fromNode == n) or (x.toNode == n) )} )
arcs = arcs.union( frozenset({Arc(a.fromNode, a.toNode, ArcWeightDatum(a.datum.weight - z)) }) )
H = DiGraph(nodes, arcs)
assignment, value = dict({}), 0
not_done = True
while( not_done ):
zwarcs = frozenset( {a for a in H.setOfArcs if a.datum.weight == 0} )
znodes = frozenset( {n.fromNode for n in zwarcs} ).union( frozenset( {n.toNode for n in zwarcs} ) )
K = DiGraph(znodes, zwarcs)
k_bipartition = bipartition(K)
matching = solve_mbm( k_bipartition )
mnodes = frozenset({a.fromNode for a in matching}).union(frozenset({a.toNode for a in matching}))
if( len(mnodes) == len(H.setOfNodes) ):
for a in matching:
assignment[ a.fromNode.uid ] = a.toNode.uid
value = sum({a.datum.weight for a in matching})
not_done = False
else:
node_cover = get_min_node_cover(matching, bipartition(K))
z = min( frozenset( {a.datum.weight for a in H.setOfArcs if a not in node_cover} ) )
nodes = H.setOfNodes
arcs1 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh-z)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) and (a.toNode not in node_cover)} )
arcs2 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh)) for a in H.setOfArcs if ( (a.fromNode not in node_cover) != (a.toNode not in node_cover)} )
arcs3 = frozenset( {Arc(a.fromNode,a.toNode,ArcWeightDatum(a.datum.weigh+z)) for a in H.setOfArcs if ( (a.fromNode in node_cover) and (a.toNode in node_cover)} )
arcs = arcs1.union(arcs2.union(arcs3))
H = DiGraph(nodes,arcs)
return value, assignment
This implementation is O(N^{5}) because it generates a new maximum matching matching at each iteration; similar to the previous two implementations of Edmonds-Karp this algorithm can be modified so that it keeps track of the matching and adapts it intelligently to each iteration. When this is done, the complexity becomes O(N^{4}). A more advanced and more recent version of this algorithm (requiring some more advanced data structures) can run in O(N^{3}). Details of both the simpler implementation above and the more advanced implementation can be found at this post which motivated this blog post.
None of the operations on arc weights modify the final assignment returned by the algorithm. Here’s why: Since our input graphs are always complete bipartite graphs a solution must map each node in one partition to another node in the second partition, via the arc between these two nodes. Notice that the operations performed on the arc weights never changes the order (ordered by weight) of the arcs incident on any particular node.
Thus when the algorithm terminates at a perfect complete bipartite matching each node is assigned a zero weight arc, since the relative order of the arcs from that node hasn’t changed during the algorithm, and since a zero weight arc is the cheapest possible arc and the perfect complete bipartite matching guarantees that one such arc exists for each node. This means that the solution generated is indeed the same as the solution from the original linear assignment problem without any modification of arc weights.
Unbalanced Assignments
It seems like the algorithm is quite limited since as described it operates only on complete bipartite graphs (those where half the nodes are in one part of the bipartition and the other half in the second part). In the worker, task motivation this means that there are as many workers as tasks (seems quite limiting).
However, there is an easy transformation that removes this restriction. Suppose that there are fewer workers than tasks, we add some dummy workers (enough to make the resulting graph a complete bipartite graph). Each dummy worker has an arc directed from the worker to each of the tasks. Each such arc has weight 0 (placing it in a matching gives no added profit). After this change the graph is a complete bipartite graph which we can solve for. Any task assigned a dummy worker is not initiated.
Suppose that there are more tasks than workers. We add some dummy tasks (enough to make the resulting graph a complete bipartite graph). Each dummy task has an arc directed from each worker to the dummy task. Each such arc has a weight of 0 (placing it in a matching gives no added profit). After this change the graph is a complete bipartite graph which we can solve for. Any worker assigned to dummy task is not employed during the period.
A Linear Assignment Example
Finally, let’s do an example with the code I’ve been using. I’m going to modify the example problem from here. We have 3 tasks: we need to clean the bathroom, sweep the floor, and wash the windows.
The workers available to use are Alice, Bob, Charlie, and Diane. Each of the workers gives us the wage they require per task. Here are the wages per worker:
| Clean the Bathroom | Sweep the Floor | Wash the Windows | |
|---|---|---|---|
| Alice | $2 | $3 | $3 |
| Bob | $3 | $2 | $3 |
| Charlie | $3 | $3 | $2 |
| Diane | $9 | $9 | $1 |
If we want to pay the least amount of money, but still get all the tasks done, who should do what task? Start by introducing a dummy task to make the digraph representing the problem bipartite.
| Clean the Bathroom | Sweep the Floor | Wash the Windows | Do Nothing | |
|---|---|---|---|---|
| Alice | $2 | $3 | $3 | $0 |
| Bob | $3 | $2 | $3 | $0 |
| Charlie | $3 | $3 | $2 | $0 |
| Diane | $9 | $9 | $1 | $0 |
Supposing that the problem is encoded in a digraph, then kuhn_munkres( bipartition(G) ) will solve the problem and return the assignment. It’s easy to verify that the optimal (lowest cost) assignment will cost $5.
Here’s a visualization of the solution the code above generates:


That is it. You now know everything you need to know about the linear assignment problem.
You can find all of the code from this article on GitHub.
Further Reading on the Toptal Blog:
Dmitri Ivanovich Arkhipov
Irvine, CA, United States
Member since January 23, 2017
About the author
Dmitri has a PhD in computer science from UC Irvine and works primarily in UNIX/Linux ecosystems. He specializes in Python and Java.
PREVIOUSLY AT


