Ensemble Methods: Elegant Techniques to Produce Improved Machine Learning Results
Machine Learning, in computing, is where art meets science. Perfecting a machine learning tool is a lot about understanding data and choosing the right algorithm. But why choose one algorithm when you can choose many and make them all work to achieve one thing: improved results.
In this article, Toptal Engineer Necati Demir walks us through some elegant techniques of ensemble methods where a combination of data splits and multiple algorithms is used to produce machine learning results with higher accuracy.
Machine Learning, in computing, is where art meets science. Perfecting a machine learning tool is a lot about understanding data and choosing the right algorithm. But why choose one algorithm when you can choose many and make them all work to achieve one thing: improved results.
In this article, Toptal Engineer Necati Demir walks us through some elegant techniques of ensemble methods where a combination of data splits and multiple algorithms is used to produce machine learning results with higher accuracy.
Necati holds a PhD degree in Machine Learning and has 14 years of experience in software development.
Expertise
Ensemble methods are techniques that create multiple models and then combine them to produce improved results. Ensemble methods in machine learning usually produce more accurate solutions than a single model would. This has been the case in a number of machine learning competitions, where the winning solutions used ensemble methods. In the popular Netflix Competition, the winner used an ensemble method to implement a powerful collaborative filtering algorithm. Another example is KDD 2009 where the winner also used ensembling. You can also find winners who used these methods in Kaggle competitions, for example here is the interview with the winner of CrowdFlower competition.
It is important that we understand a few terminologies before we continue with this article. Throughout the article I used the term “model” to describe the output of the algorithm that trained with data. This model is then used for making predictions. This algorithm can be any machine learning algorithm such as logistic regression, decision tree, etc. These models, when used as inputs of ensemble methods, are called ”base models,” and the end result is an ensemble model.
In this blog post I will cover ensemble methods for classification and describe some widely known methods of ensemble: voting, stacking, bagging and boosting.
Voting and Averaging Based Ensemble Methods
Voting and averaging are two of the easiest examples of ensemble learning in machine learning. They are both easy to understand and implement. Voting is used for classification and averaging is used for regression.
In both methods, the first step is to create multiple classification/regression models using some training dataset. Each base model can be created using different splits of the same training dataset and same algorithm, or using the same dataset with different algorithms, or any other method. The following Python-esque pseudocode shows the use of same training dataset with different algorithms.
train = load_csv("train.csv")
target = train["target"]
train = train.drop("target")
test = load_csv("test.csv")
algorithms = [logistic_regression, decision_tree_classification, ...] #for classification
algorithms = [linear_regression, decision_tree_regressor, ...] #for regression
predictions = matrix(row_length=len(target), column_length=len(algorithms))
for i,algorithm in enumerate(algorithms):
predictions[,i] = algorithm.fit(train, target).predict(test)
According to the above pseudocode, we created predictions for each model and saved them in a matrix called predictions where each column contains predictions from one model.
Majority Voting
Every model makes a prediction (votes) for each test instance and the final output prediction is the one that receives more than half of the votes. If none of the predictions get more than half of the votes, we may say that the ensemble method could not make a stable prediction for this instance. Although this is one of the more popular ensemble techniques, you may try the most voted prediction (even if that is less than half of the votes) as the final prediction. In some articles, you may see this method being called “plurality voting”.
Weighted Voting
Unlike majority voting, where each model has the same rights, we can increase the importance of one or more models. In weighted voting you count the prediction of the better models multiple times. Finding a reasonable set of weights is up to you.
Simple Averaging
In simple averaging method, for every instance of test dataset, the average predictions are calculated. This method often reduces overfit and creates a smoother regression model. The following pseudocode code shows this simple averaging method:
final_predictions = []
for row_number in len(predictions):
final_predictions.append(
mean(prediction[row_number, ])
)
Weighted Averaging
Weighted averaging is a slightly modified version of simple averaging, where the prediction of each model is multiplied by the weight and then their average is calculated. The following pseudocode code shows the weighted averaging:
weights = [..., ..., ...] #length is equal to len(algorithms)
final_predictions = []
for row_number in len(predictions):
final_predictions.append(
mean(prediction[row_number, ]*weights)
)
Stacking Multiple Machine Learning Models
Stacking, also known as stacked generalization, is an ensemble method where the models are combined using another machine learning algorithm. The basic idea is to train machine learning algorithms with training dataset and then generate a new dataset with these models. Then this new dataset is used as input for the combiner machine learning algorithm.
The pseudocode of a stacking procedure is summarized as below:
base_algorithms = [logistic_regression, decision_tree_classification, ...] #for classification
stacking_train_dataset = matrix(row_length=len(target), column_length=len(algorithms))
stacking_test_dataset = matrix(row_length=len(test), column_length=len(algorithms))
for i,base_algorithm in enumerate(base_algorithms):
stacking_train_dataset[,i] = base_algorithm.fit(train, target).predict(train)
stacking_test_dataset[,i] = base_algorithm.predict(test)
final_predictions = combiner_algorithm.fit(stacking_train_dataset, target).predict(stacking_test_dataset)
As you can see in the above pseudocode, the training dataset for combiner algorithm is generated using the outputs of the base algorithms. In the pseudocode, the base algorithm is generated using training dataset and then the same dataset is used again to make predictions. But as we know, in the real world we do not use the same training dataset for prediction, so to overcome this problem you may see some implementations of stacking where training dataset is splitted. Below you can see a pseudocode where the training dataset is split before training the base algorithms:
base_algorithms = [logistic_regression, decision_tree_classification, ...] #for classification
stacking_train_dataset = matrix(row_length=len(target), column_length=len(algorithms))
stacking_test_dataset = matrix(row_length=len(test), column_length=len(algorithms))
for i,base_algorithm in enumerate(base_algorithms):
for trainix, testix in split(train, k=10): #you may use sklearn.cross_validation.KFold of sklearn library
stacking_train_dataset[testcv,i] = base_algorithm.fit(train[trainix], target[trainix]).predict(train[testix])
stacking_test_dataset[,i] = base_algorithm.fit(train).predict(test)
final_predictions = combiner_algorithm.fit(stacking_train_dataset, target).predict(stacking_test_dataset)
Bootstrap Aggregating
The name Bootstrap Aggregating, also known as “Bagging”, summarizes the key elements of this strategy. In the bagging algorithm, the first step involves creating multiple models. These models are generated using the same algorithm with random sub-samples of the dataset which are drawn from the original dataset randomly with bootstrap sampling method. In bootstrap sampling, some original examples appear more than once and some original examples are not present in the sample. If you want to create a sub-dataset with m elements, you should select a random element from the original dataset m times. And if the goal is generating n dataset, you follow this step n times.
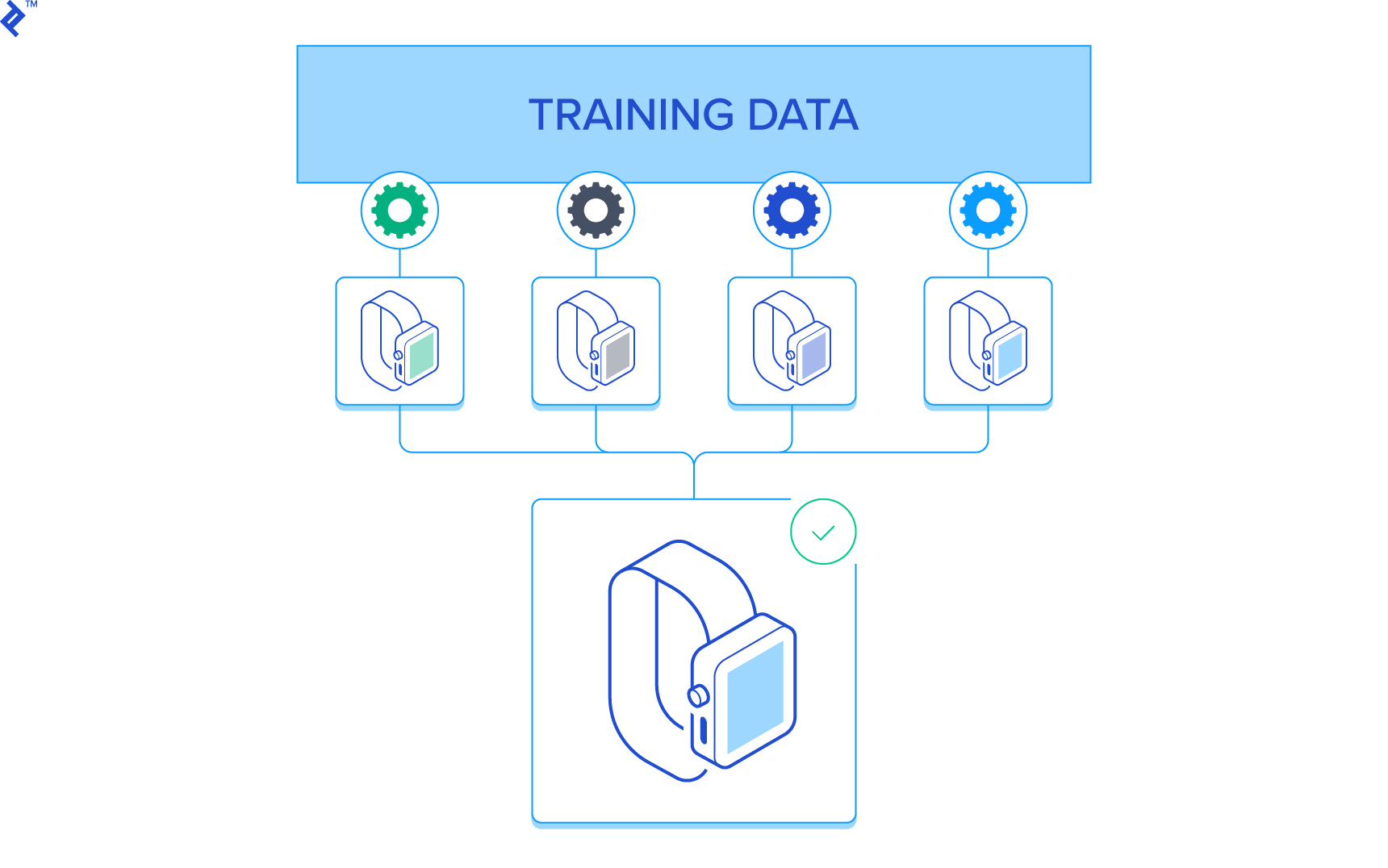
At the end, we have n datasets where the number of elements in each dataset is m. The following Python-esque pseudocode show bootstrap sampling:
def bootstrap_sample(original_dataset, m):
sub_dataset = []
for i in range(m):
sub_dataset.append(
random_one_element(original_dataset)
)
return sub_dataset
The second step in bagging is aggregating the generated models. Well known methods, such as voting and averaging, are used for this purpose.
The overall pseudocode look like this:
def bagging(n, m, base_algorithm, train_dataset, target, test_dataset):
predictions = matrix(row_length=len(target), column_length=n)
for i in range(n):
sub_dataset = bootstrap_sample(train_dataset, m)
predictions[,i] = base_algorithm.fit(original_dataset, target).predict(test_dataset)
final_predictions = voting(predictions) # for classification
final_predictions = averaging(predictions) # for regression
return final_predictions
In bagging, each sub-samples can be generated independently from each other. So generation and training can be done in parallel.
You can also find implementation of the bagging strategy in some algorithms. For example, Random Forest algorithm uses the bagging technique with some differences. Random Forest uses random feature selection, and the base algorithm of it is a decision tree algorithm.
Boosting: Converting Weak Models to Strong Ones
The term “boosting” is used to describe a family of algorithms which are able to convert weak models to strong models. The model is weak if it has a substantial error rate, but the performance is not random (resulting in an error rate of 0.5 for binary classification). Boosting incrementally builds an ensemble by training each model with the same dataset but where the weights of instances are adjusted according to the error of the last prediction. The main idea is forcing the models to focus on the instances which are hard. Unlike bagging, boosting is a sequential method, and so you can not use parallel operations here.
The general procedure of the boosting algorithm is defined as follows:
def adjust_dataset(_train, errors):
#create a new dataset by using the hardest instances
ix = get_highest_errors_index(train)
return concat(_train[ix], random_select(train))
models = []
_train = random_select(train)
for i in range(n): #n rounds
model = base_algorithm.fit(_train)
predictions = model.predict(_train)
models.append(model)
errors = calculate_error(predictions)
_train = adjust_dataset(_train, errors)
final_predictions = combine(models, test)
The adjust_dataset function returns a new dataset containing the hardest instances, which can then be used to force the base algorithm to learn from.
Adaboost is a widely known algorithm which is a boosting method. The founders of Adaboost won the Gödel Prize for their work. Mostly, decision tree algorithm is preferred as a base algorithm for Adaboost and in sklearn library the default base algorithm for Adaboost is decision tree (AdaBoostRegressor and AdaBoostClassifier). As we discussed in the previous paragraph, the same incremental method applies for Adaboost. Information gathered at each step of the AdaBoost algorithm about the ‘hardness’ of each training sample is fed into the model. The ‘adjusting dataset’ step is different from the one described above and the ‘combining models’ step is calculated by using weighted voting.
Conclusion
Although ensemble methods can help you win machine learning competitions by devising sophisticated algorithms and producing results with high accuracy, it is often not preferred in the industries where interpretability is more important. Nonetheless, the effectiveness of these methods are undeniable, and their benefits in appropriate applications can be tremendous. In fields such as healthcare, even the smallest amount of improvement in the accuracy of machine learning algorithms can be something truly valuable.
Further Reading on the Toptal Blog:
Summit, NJ, United States
Member since November 17, 2015
About the author
Necati holds a PhD degree in Machine Learning and has 14 years of experience in software development.