Una Introducción a la Teoría y Complejidad de la Computabilidad
¿Qué es una computadora? ¿Cuáles son las limitaciones de una computadora? ¿Hay problemas que una computadora no puede resolver?
En este artículo, Mehmet Bajin, ingeniero de software freelance de Toptal, explora los fundamentos de la computación y el impacto que tienen en la computabilidad y su complejidad.
¿Qué es una computadora? ¿Cuáles son las limitaciones de una computadora? ¿Hay problemas que una computadora no puede resolver?
En este artículo, Mehmet Bajin, ingeniero de software freelance de Toptal, explora los fundamentos de la computación y el impacto que tienen en la computabilidad y su complejidad.

Mehmet Bajin
With experience at Google, Exxon, and a Master’s in CS, Mehmet’s deep expertise serves him well as a full-stack javascript developer.
Previously At

Te has preguntado alguna vez: ¿Cuál es exactamente el dispositivo en el que estás leyendo este artículo? ¿Qué es una computadora? La ciencia de la computación se remonta a un tiempo mucho antes de que se pensara en estos modernos dispositivos informáticos. En una industria donde las preguntas más frecuentes giran en torno a los lenguajes de programación, marcos y bibliotecas, a menudo damos por sentado los conceptos fundamentales que hacen funcionar una computadora.
Pero estas computadoras, que parecen poseer un potencial infinito— ¿tienen alguna limitación? ¿Hay problemas que las computadoras no pueden resolver?

En este artículo, abordaremos estas preguntas alejándonos de los detalles de los lenguajes de programación y las arquitecturas de la computadora. Al comprender el poder y las limitaciones de las computadoras y los algoritmos, podemos mejorar la forma en que pensamos y razonar mejor sobre las diferentes estrategias.
La visión abstracta de la informática produce resultados que han resistido la prueba del tiempo, siendo tan valiosos para nosotros hoy como lo fueron cuando se desarrollaron inicialmente en la década de 1970.
Computabilidad
¿Qué es una computadora? ¿Qué es un problema?
En la escuela, a menudo se nos enseña un modelo mental de problemas y funciones que dice algo como esto:
Una función es un procedimiento que aplica a una entrada x para encontrar una salida f(x).
Resulta que la definición matemática es diferente:
Una función es un conjunto de pares ordenados de modo que el primer elemento de cada par proviene de un conjunto X (llamado el dominio), el segundo elemento de cada par proviene de un conjunto Y (llamado co-dominio o rango) y cada elemento del dominio está emparejado con exactamente un elemento del rango.
Eso fue bastante. Pero, ¿qué significa eso exactamente?
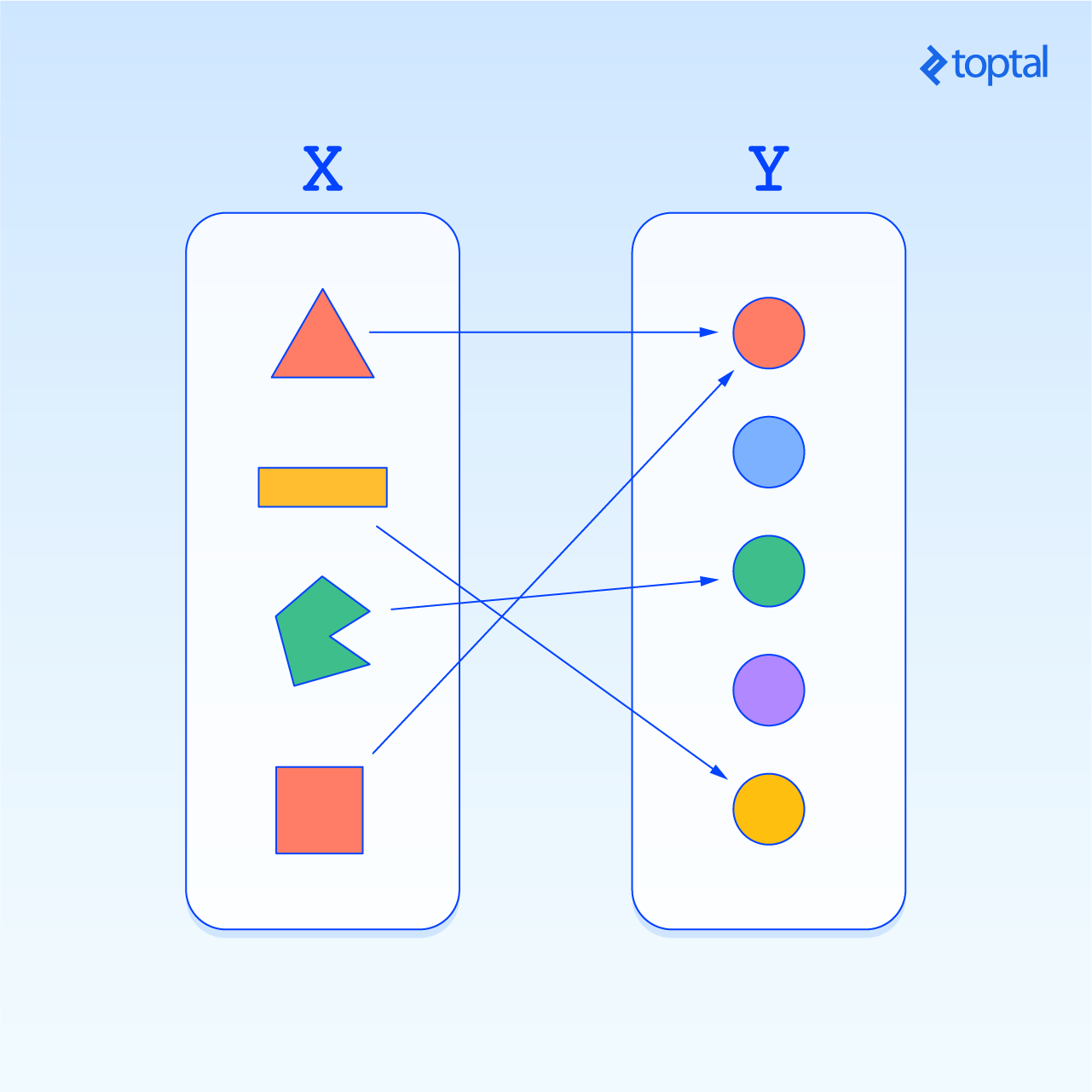
Esta definición nos dice que una computadora es una máquina para funciones informáticas.
¿Por qué?
Porque las computadoras transforman la entrada arbitraria a alguna salida. En otras palabras, resuelven problemas. Las dos definiciones de funciones, la que conocemos muy bien y la formal, coinciden para muchos propósitos prácticos.
Sin embargo, la definición matemática nos permite llegar a conclusiones interesantes tales como la existencia de funciones no procesables (es decir, problemas sin solución):
Por qué no todas las funciones se pueden describir como un algoritmo.
Reglas del Juego
Para ayudar con nuestros argumentos, imaginemos a las computadoras como máquinas que tienen una entrada, desarrollan una secuencia de operaciones y después de un tiempo, dan una salida.
Vamos a llamar a la entrada alfabeto de la máquina, que es un set de secuencia de caracteres de algún conjunto finito. Por ejemplo, el alfabeto de la máquina puede ser binario (0s y 1s) o podría ser el juego de caracteres ASCII. Cualquier secuencia finita de caracteres es una cadena—por ejemplo “0110.”
Además, representaremos el resultado de una máquina como una decisión binaria de aceptación y rechazo que se entrega una vez que la máquina (con suerte) finaliza su cálculo. Esta abstracción se ajusta bien a la definición matemática de funciones anteriores.

Dados estos parámetros, es importante caracterizar un tipo más: una colección de cadenas de caracteres. Tal vez nos preocupamos por el conjunto de cadenas de caracteres que acepta una máquina, o tal vez estamos construyendo una máquina que acepta cadenas de caracteres en un determinado conjunto y no en otros, o tal vez estamos preguntando si es posible diseñar una máquina que acepte todo en algún conjunto particular y no en otros.
En todos estos casos, un conjunto de cadenas de caracteres se denomina lenguaje—por ejemplo, el conjunto de todas las cadenas binarias que representan números pares o el conjunto de cadenas que tienen un número par de caracteres. Resulta que los idiomas, como los números, pueden ser operados con los operadores como concatenación, unión, intersección y otros similares.
Un operador importante es el operador estrella Kleene que también se usa con expresiones regulares. Esto se puede considerar como la unión de todos los poderes posibles del lenguaje. Por ejemplo, si nuestro idioma A es el conjunto de cadenas de caracteres { ‘01’, ‘1’ }, entonces un miembro de A* es la cadena de caracteres ‘0101111’.
Contabilidad
La última pieza del rompecabezas antes de demostrar nuestra afirmación de que no todas las funciones son computables es el concepto de contabilización. Intuitivamente, nuestra prueba mostrará que hay más idiomas; es decir, más problemas que posibles programas para resolverlos. Esto funciona porque el tema de si una cadena de caracteres pertenece a un idioma (Sí/No) es en sí misma un problema.
Más precisamente, nuestra prueba afirma que el conjunto de posibles programas es infinitamente contable, mientras que el conjunto de idiomas sobre un alfabeto es infinitamente incontable.
En este punto, puedes estar pensando “La infinidad es una idea bastante extraña en sí misma, ¡ahora tengo que lidiar con dos de ellos!”
Bueno, no es tan malo. Un conjunto contablemente infinito es uno que se puede enumerar. Es posible decir: este es el primer elemento, este es el segundo elemento y así sucesivamente, eventualmente asignando un número a cada elemento del conjunto. Toma el conjunto de números pares, por ejemplo. Podemos decir que 2 es el primero, 4 el segundo, 6 el tercero y así sucesivamente. Tales conjuntos son contablemente infinitos o contables.
Sin embargo, con algunos conjuntos como los números reales, no importa cuán inteligente seas; simplemente no hay enumeración. Estos conjuntos son incontablemente infinitos o incontables.
Muchos Programas de Manera Contable
Primero queremos mostrar que el conjunto de programas de computadora es contable. Para nuestros propósitos, hacemos esto al observar que el conjunto de todas las cadenas de caracteres sobre un alfabeto finito es contable. Esto funciona porque los programas de computadora son cadenas de caracteres finitas.
La prueba es sencilla y no cubrimos los detalles aquí. El punto clave es que hay tantos programas de computadora como, por ejemplo, números naturales.
Para reiterar:
El conjunto de todas las cadenas de caracteres sobre cualquier alfabeto (Ej., Conjunto de todos los programas informáticos) es contable.
Incontablemente, Muchos Idiomas
Dada esta conclusión, ¿qué pasa con los subconjuntos de estas cadenas de caracteres? Preguntado de otra manera, ¿qué pasa con el conjunto de todos los idiomas? Resulta que este conjunto es incontable.
El conjunto de todos los idiomas sobre cualquier alfabeto es incontable.
Una vez más, no cubrimos la prueba aquí.
Consecuencias
Aunque pueden no ser inmediatamente aparentes, las consecuencias de la incontabilidad de los idiomas y la contabilización del conjunto de todos los programas informáticos son profundas.
¿Por qué?
Supongamos que A es el conjunto de caracteres ASCII; los caracteres ASCII son solo los necesarios para componer un programa de computadora. Podemos ver que el conjunto de cadenas de caracteres que representan, por ejemplo, los programas de JavaScript son un subconjunto de A* (aquí, * es el operador estrella de Kleene). La elección de JavaScript es arbitraria. Dado que este conjunto de programas es un subconjunto de un conjunto contable, tenemos que el conjunto de programas de JavaScript es contable.
Además, consideremos que para cualquier idioma L podemos definir alguna función f que evalúe a 1 si alguna cadena x está en L y 0 en caso contrario. Todas esas funciones son distintas. Debido a que existe una correspondencia 1:1 con el conjunto de todos los idiomas y porque el conjunto de todos los idiomas es incontable, tenemos que el conjunto de todas esas funciones es incontable.
Aquí está el punto en profundidad:
Como el conjunto de todos los programas válidos es contable pero el conjunto de funciones no lo es, entonces debe haber algunas funciones para las cuales simplemente no podemos escribir programas.
Todavía no sabemos cómo son estas funciones o problemas pero sabemos que existen. Ésta es una realización humillante porque hay algunos problemas por los cuales no hay solución. Consideramos que las computadoras son extremadamente poderosas y capaces sin embargo, algunas cosas están fuera de su alcance.
Ahora la pregunta es: “¿Cómo son estos problemas?” Antes de continuar describiendo estos problemas, primero debemos modelar la computación de forma generalizada.
Máquinas de Turing
Uno de los primeros modelos matemáticos de una computadora fue desarrollado por Alan Turing. Este modelo, llamado máquina de Turing, es un dispositivo extremadamente simple que captura por completo nuestra noción de computabilidad.
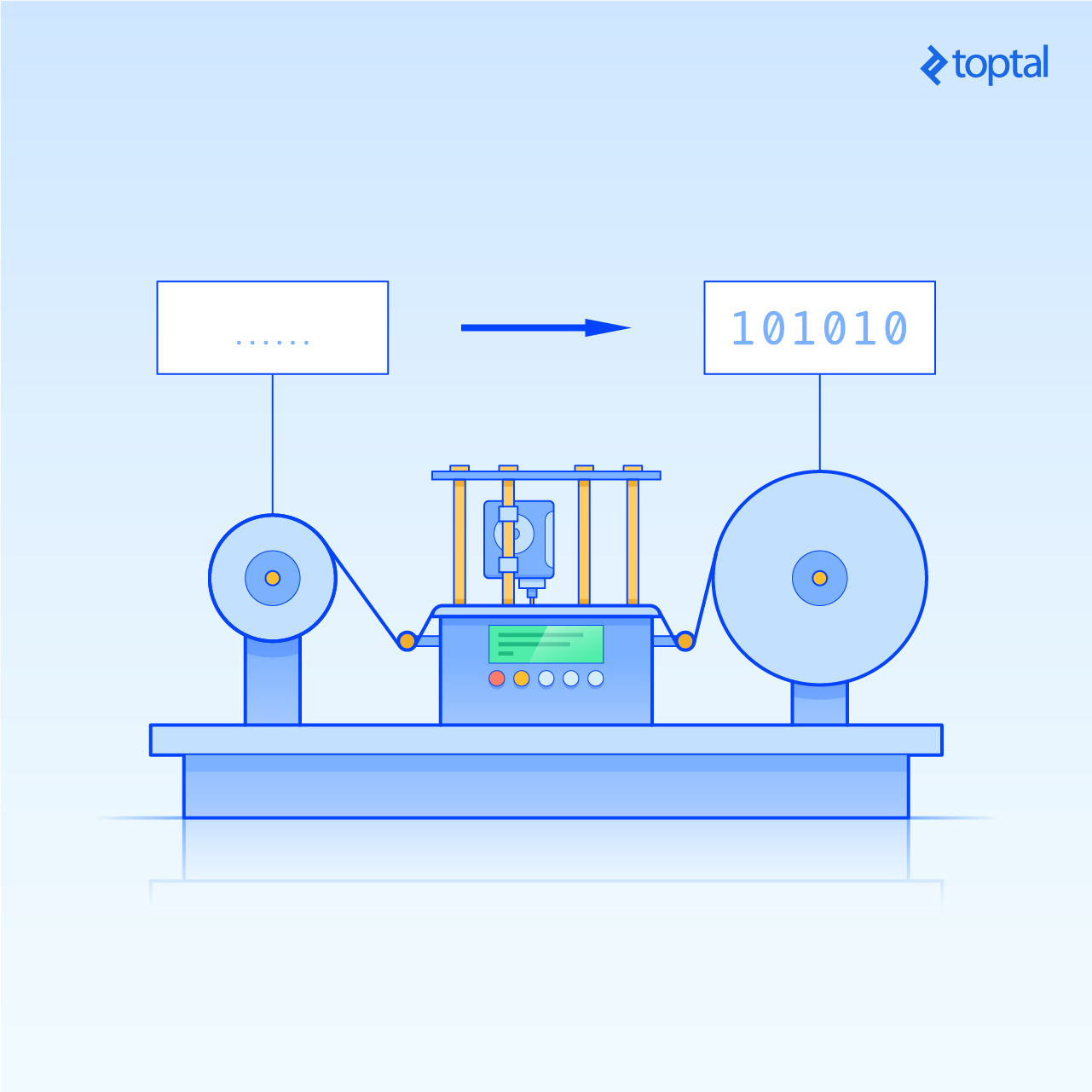
La entrada a la máquina es una cinta sobre la cual se ha escrito la entrada. Usando un cabezal de lectura/escritura, la máquina convierte la entrada en salida a través de una serie de pasos. En cada paso, se toma una decisión sobre si y qué escribir en la cinta y si se debe mover hacia la derecha o hacia la izquierda. Esta decisión se basa exactamente en dos cosas:
-
El símbolo actual debajo del cabezal y
-
El estado interno de la máquina, que también se actualiza cuando se escribe el símbolo
Eso es todo.
Universalidad
En 1926, Alan Turing no solo desarrolló la máquina de Turing sino que también tuvo varias ideas importantes sobre la naturaleza de la computación cuando escribió su famoso artículo, “Sobre números computables”. Se dio cuenta de que un programa de computadora en sí podría considerarse como entrada a una computadora. Con este punto de vista, tuvo la hermosa idea de que una máquina de Turing podría simular o ejecutar esa entrada.
Si bien damos por sentadas estas ideas hoy, en la época de Turing la idea de una máquina tan universal fue el gran avance que permitió a Turing desarrollar problemas sin solución.
Tesis de Church-Turing
Antes de continuar, examinemos un punto importante: sabemos que la máquina de Turing es un modelo de computación, pero ¿es lo suficientemente general? Para responder a esta pregunta, pasamos a la Tesis de Church-Turing, lo que da credibilidad a la siguiente declaración:
Todo lo computable es computable por una máquina de Turing.
Mientras Turing desarrolló la máquina de Turing como un modelo de computación, Alonzo Church también desarrolló un modelo de cálculo conocido como lambda-cálculo. Estos modelos son potentes ya que ambos describen la computación y lo hacen de una manera igual a cualquiera de las computadoras de hoy o para cualquier computadora. Esto significa que podemos usar una máquina de Turing para describir los problemas irresolubles que buscamos, sabiendo que nuestros hallazgos se aplicarán a todas las computadoras posibles.
Reconocimiento y Decidibilidad
Tenemos que cubrir un poco más de fondo antes de describir concretamente un problema sin solución, a saber, los conceptos de reconocedores de lenguaje y factores decisivos de lenguaje.
Un idioma es reconocible si hay una máquina de Turing que lo reconoce.
y
Un lenguaje es decidible si hay una máquina de Turing que lo decide.
Para ser un reconocedor de un idioma, una máquina de Turing debe aceptar cada cadena de caracteres en el idioma y no debe aceptar nada que no esté en el idioma. Puede rechazar o repetir esas cadenas. Para ser un factor de decisión, una máquina de Turing siempre debe detener su entrada aceptando o rechazando.
Aquí, la idea de detener la entrada es crítica. De hecho, vemos que los factores de decisión son más poderosos que los reconocedores. Además, un problema se puede resolver, o dicho de otra manera, una función es decidible solo si existe una máquina de Turing que decide el lenguaje descrito por la función.
Indecibilidad
Si alguna vez has escrito un programa de computadora, seguramente debes saber la sensación de estar sentado allí, solo mirando la computadora girar las ruedas cuando se ejecuta el programa. No se sabe si el programa tarda mucho o si hay algún error en el código que causa un ciclo infinito. Es posible que incluso te hayas preguntado por qué el compilador no verifica el código para ver si se detendría o se repetirá para siempre cuando se ejecute.
El compilador no tiene dicho control porque simplemente no se puede hacer. No es que los ingenieros de compilación no sean lo suficientemente inteligentes o carezcan de los recursos, es simplemente imposible verificar un programa de computadora arbitrario para determinar si se detiene.
Podemos probar esto usando la máquina de Turing. Las máquinas de Turing se pueden describir como cadenas de caracteres, por lo que hay un número contable de ellas. Supongamos que M1, M2, y así sucesivamente conforman el conjunto de todas las máquinas de Turing. Vamos a definir la siguiente función:
Aquí, <M> es la sintaxis para la “codificación de cadena de M” y esta función representa el problema de producir 1 si Mi se detiene al aceptar Mj como entrada y salida 0 al contrario. Ten en cuenta que Mi debe detener (es decir, ser un factor decisivo). Esto es necesario ya que deseamos describir una función indecidible (es decir, problema sin solución).
Ahora, definamos también un lenguaje L que consiste en codificaciones de cadenas de máquinas de Turing que NO aceptan sus propias descripciones:
Por ejemplo, alguna máquina M1 puede dar en la salida 0 para la entrada <M1>, mientras que otra máquina M2 puede dar en la salida 1 para la entrada <M2>. Para probar que este lenguaje es indecidible, preguntamos qué hace ML, la máquina que decide el lenguaje L, cuando se le da su propia descripción <ML> como entrada. Hay dos oportunidades:
ML acepta <ML>
o
ML rechaza <ML>
Si ML acepta su propia codificación, entonces eso significa que <ML> no está en el idioma L. Sin embargo, si ese fuera el caso, entonces ML no debería haber aceptado su codificación en primer lugar. Por otro lado, si ML no acepta su propia codificación, entonces <ML> está en el lenguaje L, entonces ML debería haber aceptado su codificación de cadena de caracteres.
En ambos casos, tenemos una paradoja o, en términos matemáticos, una contradicción, que demuestra que el lenguaje L es indecidible; por lo tanto, hemos descrito nuestro primer problema sin solución.
Deteniendo el Problema
Si bien el problema que acabamos de describir puede no parecer relevante, puede reducirse a problemas adicionales irresolubles de importancia práctica, sobre todo el problema de detención:
El lenguaje de las codificaciones de las máquinas de Turing que se detienen en la cadena vacía.
El problema de detención se aplica a la pregunta de por qué los compiladores no pueden detectar nudos infinitos desde antes. Si no podemos determinar si un programa termina en la cadena vacía, entonces ¿cómo podríamos determinar si su ejecución daría como resultado un nudo infinito? En este punto podría parecer que agitamos nuestras manos para llegar a una conclusión simple sin embargo, nos dimos cuenta de que ninguna máquina de Turing puede decir si un programa de computadora se detendrá o permanecerá en un nudo para siempre. Este es un problema importante con aplicaciones prácticas y no se puede resolver en una máquina de Turing o cualquier otro tipo de computadora. Un iPhone no puede resolver este problema. Un escritorio con muchos núcleos no puede resolver este problema. La nube no puede resolver este problema. Incluso si alguien quisiera inventar una computadora cuántica, aún no sería capaz de resolver el problema de detención.
Resumen
En nuestro examen de la teoría de computabilidad hemos visto cómo hay muchas funciones que no son computables en ningún sentido ordinario de la palabra mediante un argumento de conteo. Definimos con precisión lo que queremos decir con computación, remontándonos a la inspiración de Turing a partir de su propia experiencia con lápiz y papel para formalizar la máquina de Turing. Hemos visto cómo este modelo puede calcular cualquier cosa que cualquier computadora actual o prevista para mañana pueda y nos dimos cuenta de una clase de problemas que no son computables en absoluto.
Aun así, la computabilidad tiene una desventaja. El hecho de que podamos resolver un problema no significa que podamos resolverlo rápidamente. Después de todo, ¿de qué sirve una computadora si su cálculo no va a terminar antes de que el sol se vuelva nova sobre nosotros decenas de millones de años en el futuro?
Dejando las funciones computables y los lenguajes atrás, ahora discutimos la complejidad de cómputo, examinando el cálculo eficiente y el famoso problema P vs. NP.
Complejidad
Lento vs. Rápido
Los científicos informáticos reconocen una variedad de clases de problemas y dos clases que nos importan incluyen problemas que las computadoras pueden resolver rápida o eficientemente, conocidos como P y problemas cuyas soluciones se pueden verificar rápidamente pero no se pueden obtener rápidamente, conocidas como NP.
Por ejemplo, supongamos que eres responsable de desarrollar algoritmos para un servicio de citas en línea y alguien plantea la pregunta: “¿Todos pueden obtener una cita?” La respuesta se reduce a emparejar individuos compatibles para que todos estén emparejados. Resulta que hay algoritmos eficientes para resolver este problema. Este problema está en el conjunto P.
Bueno, ¿y si quisiéramos identificar la hermandad más grande entre nuestros usuarios? Por hermandad, nos referimos a la red más grande de individuos que son compatibles entre sí. Cuando el recuento de usuarios es bajo, este problema se puede resolver rápidamente. Podemos identificar fácilmente, por ejemplo, una hermandad con 3 usuarios. Sin embargo, a medida que empezamos a buscar hermandades más grandes, el problema se vuelve cada vez más difícil de resolver. Este problema está en el conjunto NP.
Definiciones Formales
P es el conjunto de problemas que se pueden resolver en tiempo polinomial. Es decir, el número de pasos computacionales está limitado por una función polinómica con respecto al tamaño del problema. Sabemos que la pregunta “¿Todos pueden tener una cita?”, también conocida como problema de coincidencia bipartita, está en P.
NP es el conjunto de problemas que son verificables en tiempo polinomial. Esto incluye todos los problemas en P, por supuesto; sin embargo, no sabemos si esta contención es estricta. Conocemos problemas que son verificables de manera eficiente pero que no se pueden resolver de manera eficiente, pero no sabemos si el problema es verdaderamente insoluble. El problema de la hermandad es uno de esos problemas. Sabemos que podemos verificar la solución de manera eficiente pero no sabemos con certeza si podemos resolver el problema de manera eficiente.
Por último, NP-complete es el conjunto de problemas que son los problemas más difíciles en NP. Se les conoce como los más difíciles porque cualquier problema en NP se puede transformar eficientemente en NPC. Como resultado, si alguien identificara una solución eficiente a un problema en NPC, toda la clase de NP sería absorbida por P. El problema de la hermandad también está en NPC
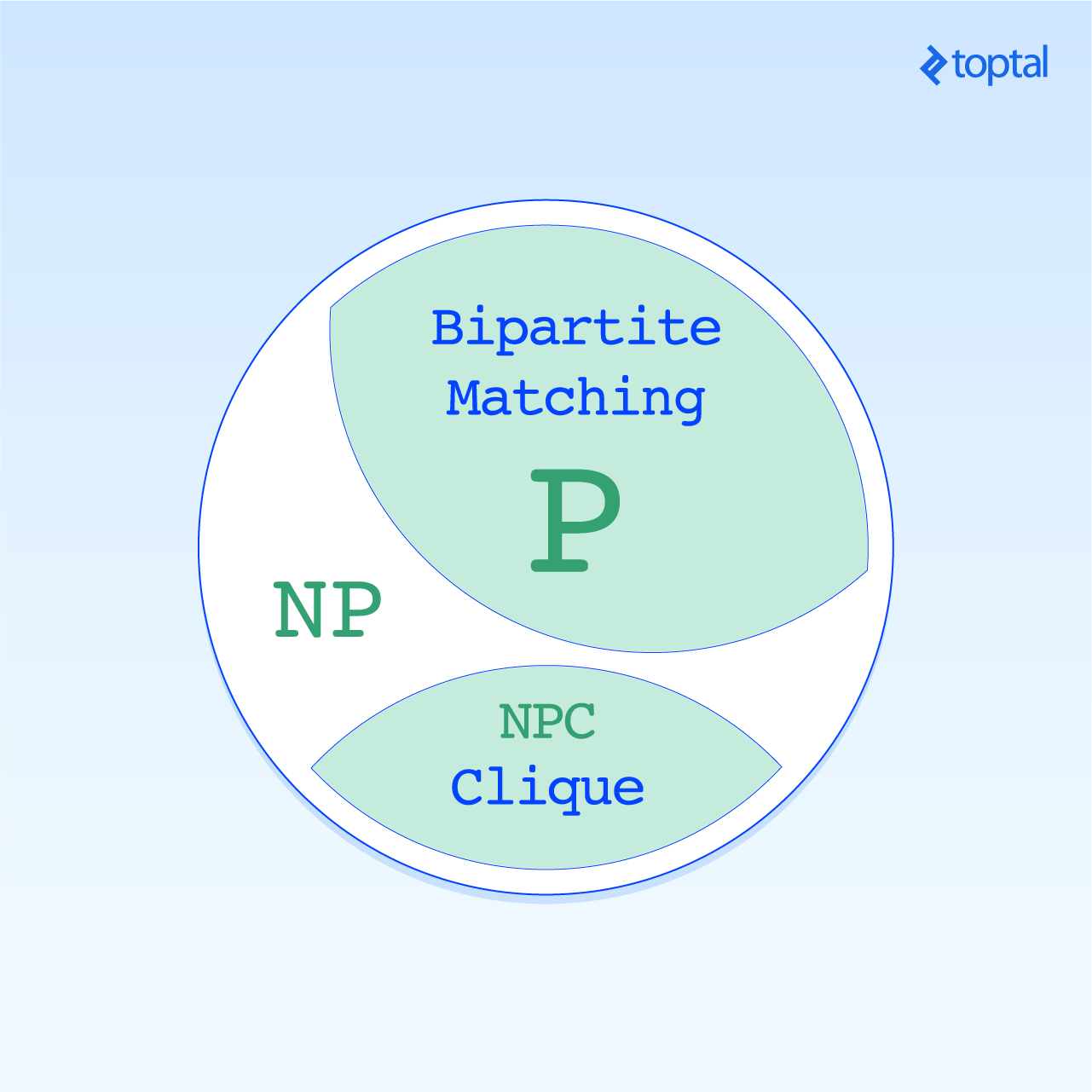
Por lo tanto, llegamos al problema de P contra NP. Muchos científicos informáticos y matemáticos creen firmemente que P y NP no son iguales. Si lo fueran, las implicaciones serían más allá de lo profundo. Gran parte de la infraestructura digital actual se basa en el hecho de que hay problemas en NP que no están en P. Si ese no fuera el caso, los métodos criptográficos por ejemplo, colapsarían de la noche a la mañana, permitiendo que una persona que posee una solución eficiente a un problema de NPC pueda subvertir incluso los protocolos de seguridad más estrictos.
Sutilezas de Trazabilidad
Para los principiantes en informática, la diferencia entre los problemas de emparejamiento y hermandad no parece ser un gran problema. De hecho, la diferencia entre un problema en P y un problema en NP puede ser muy sutil. Ser capaz de notar la diferencia es importante para cualquiera que diseñe algoritmos en el mundo real.
Considera el problema de la ruta más corta. Dadas dos ubicaciones, el objetivo es identificar el camino más corto entre ellas. Un iPhone calcula esto en cuestión de milisegundos. Este es un problema computacionalmente tratable.
Por otro lado, considera el problema del vendedor ambulante, donde el objetivo es visitar un subconjunto de posibles destinos que terminan en el origen mientras viajan la distancia más corta posible. Este problema es similar al problema de ruta más corta pero es NP-completo; también explica por qué la logística de la cadena de suministro es una industria de mil millones de dólares.
De hecho, podemos ser aún más sutiles. En lugar de pedir el camino más corto (P), podemos pedir el camino más largo sin nudos. Resulta que el problema de la ruta más larga también es NP-completo.
Hay muchos más ejemplos de esta sutil distinción, incluida la identificación de las coberturas de los vértices en los gráficos bipartitos vs. generales o la satisfacción de las fórmulas booleanas con dos y tres literales por cláusula. El punto es que no es inmediatamente obvio si un problema está en P o NP, por ello la razón del análisis del tiempo de ejecución es una habilidad crítica. Si el algoritmo que uno debe diseñar es para un problema en P, entonces sabemos que hay una solución eficiente. Si, por otro lado, el problema está en NP, entonces tenemos un caso fuerte para argumentar en contra de buscar una solución, porque el algoritmo en general, simplemente tomaría demasiado tiempo para resolver el problema.
Resumen
En este examen de complejidad, definimos las clases de problemas P y NP. P informalmente representa problemas que pueden ser resueltos eficientemente por una computadora, mientras que NP representa aquellos que son verificables de manera eficiente.
Nadie ha podido demostrar que P no es igual a NP. Si estas dos clases de problemas son equivalentes, es lo que se conoce como el problema P vs. NP y es el problema abierto más importante en la informática teórica actual, si no en todas las matemáticas. De hecho, en el año 2000, el Clay Math Institute denominó al problema P vs. NP como una de las siete preguntas abiertas más importantes en matemáticas y ha ofrecido una recompensa de un millón de dólares por una prueba que determina la solución a este problema.
Conclusión
En este artículo nos adentramos en los ámbitos de la computabilidad y la complejidad, respondiendo grandes preguntas como “¿Qué es una computadora?”. Si bien los detalles pueden ser abrumadores, hay una serie de aprendizajes profundos que vale la pena recordar:
-
Hay algunas cosas que simplemente no se pueden calcular, como el problema de detención.
-
Hay algunas cosas que no se pueden calcular de manera eficiente, como los problemas en NPC.
Más importantes que los detalles son las formas de pensar sobre computación y problemas computacionales. En nuestra vida profesional e incluso en nuestro día a día, podemos encontrarnos con problemas nunca antes vistos y podemos usar herramientas y técnicas probadas para determinar el mejor curso de acción.
